Lecture 03

Linear Regression Model with Stan

Jihong Zhang

Educational Statistics and Research Methods

Today’s Lecture Objectives

1. An Introduction to MCMC

2. An Introduction to Stan

3. Example: Linear Regression

but, before we begin…

1. Go through qmd file Lecture03.qmd;
2. Download R file DietDataExample.R and data file DietData.csv

Quiz:

1. What is a conjugate prior?
2. Why we want to use conjugate priors?

In previous class…

1. We work with a simplest Bayesian model: roll “1” from a 6-size dice
2. We talked about the selection of prior distributions from uninformative to informative priors
3. We talked about binomial distribution as the likelihood function
4. The posterior distribution is directly derived by update \(\alpha\) and \(\beta\)

Markov Chain Monte Carlo Estimation

Today, we dive deeper into the estimation process.

1. Bayesian analysis is all about estimating the posterior distribution.
2. Up until now, we’ve worked with the posterior distribution that are well-known

   • Beta-Binomial conjugate pairs had a Beta posterior distribution

   • In general, likelihood distributions from the exponential family have conjugate priors

   • Conjugate prior: the family of the prior is equivalent to the family of posterior.

Why not keep using conjugate priors for all scenarios?

• Oftentimes, however, posterior distributions are not easily obtainable
  • No longer able to use properties of the distribution to estimate parameters
• It is possible to use an optimization algorithm (e..g., Newton-Raphson or Expectation-Maximization) to find maximum value of posterior distribution
  • But, such algorithms may be very time consuming for high-dimensional problems
• Instead: “sketch” the posterior by sampling from it - then use that sketch to make inference
  • Sampling is done via MCMC

MCMC algorithm

1. MCMC algorithm interactively draws samples from the posterior distribution
   • For fairly simplistic models, each iteration has independent samples
   • Most models have some layers of dependency included
     • which can slow down the sample process from the posterior distribution
   • One problem of slowness of MCMC is high-dimensional problems
2. This plot shows one variant of MCMC - Metropolis sampling draws for two highly correlated parameters

Metropolis chains under high correlations

Variations of MCMC algorithms

• Most of these specific algorithms use one of two types sampling:
  1. Direct sampling from the posterior distribution (i.e., Gibbs sampling)
     • Often used when conjugate priors are specified
     • Popular software: BUGS, JAGS, Mplus
  2. Indirect (rejection-based) sampling from the posterior distribution (e.g, Metropolis-Hastings, Hamiltonian Monte Carlo)
     • Popular software: Stan

Making MCMC Algorithms

• Efficiency is the main reason for many algorithms
  • Efficiency in this context: How quickly the algorithm converges and provides adequate coverage (“sketching”) of the posterior distribution
  • No one algorithm is uniformly most efficient for all models (here model = likelihood \(\times\) prior)
• The good news is that many software packages (stan, JAGS, Mplus, especially) don’t make you choose which specific algorithm to use
• The bad news is that sometimes your model may take a large amount of time to reach convergence (think days or weaks)
• Alternatively, you can code your own custom algorithm to make things run smoother (different priors/ sampling strategies)

Commonalities Across MCMC Algorithms

• Despite having fairly broad differences regarding how algorithms sample from the posterior distribution, there are quite a few things that are similar across algorithms:

  1. A period of the Markov chain where sampling is not directly from the posterior

     • The burnin period (sometimes coupled with other tuning periods and called warmup)

  2. Methods used to assess convergence of the chain to the posterior distribution

     • Often involving the need to use multiple chains with independent and differing starting values

  3. Summaries of the posterior distribution

• Further, rejection-based sampling algorithms (e.g., Metropolis) often need a tuning period to make the sampling more efficient

  • The tuning period comes before the algorithm begins its burnin period

MCMC Demonstration

• To demonstrate each type of algorithm, we will use a model for a normal distribution

  1. We will investigate each, brief

  2. We will then switch over to stan to show the syntax and let stan work

  3. Finnaly, we will conclude by talking about assessing convergence and how to report parameter estimates

Example Data: Post-Diet Weights

Download example data UCLA website

Information about data:

• In this example data file, it contains 30 subjects who used one of three diets: diet 1 (diet=1), diet 2 (diet=2), and a control group (diet=3).
• The file DietData.csv contains the data we needed.
• Variables in the data set are:
  1. Respondent: Respondent ID 1-30
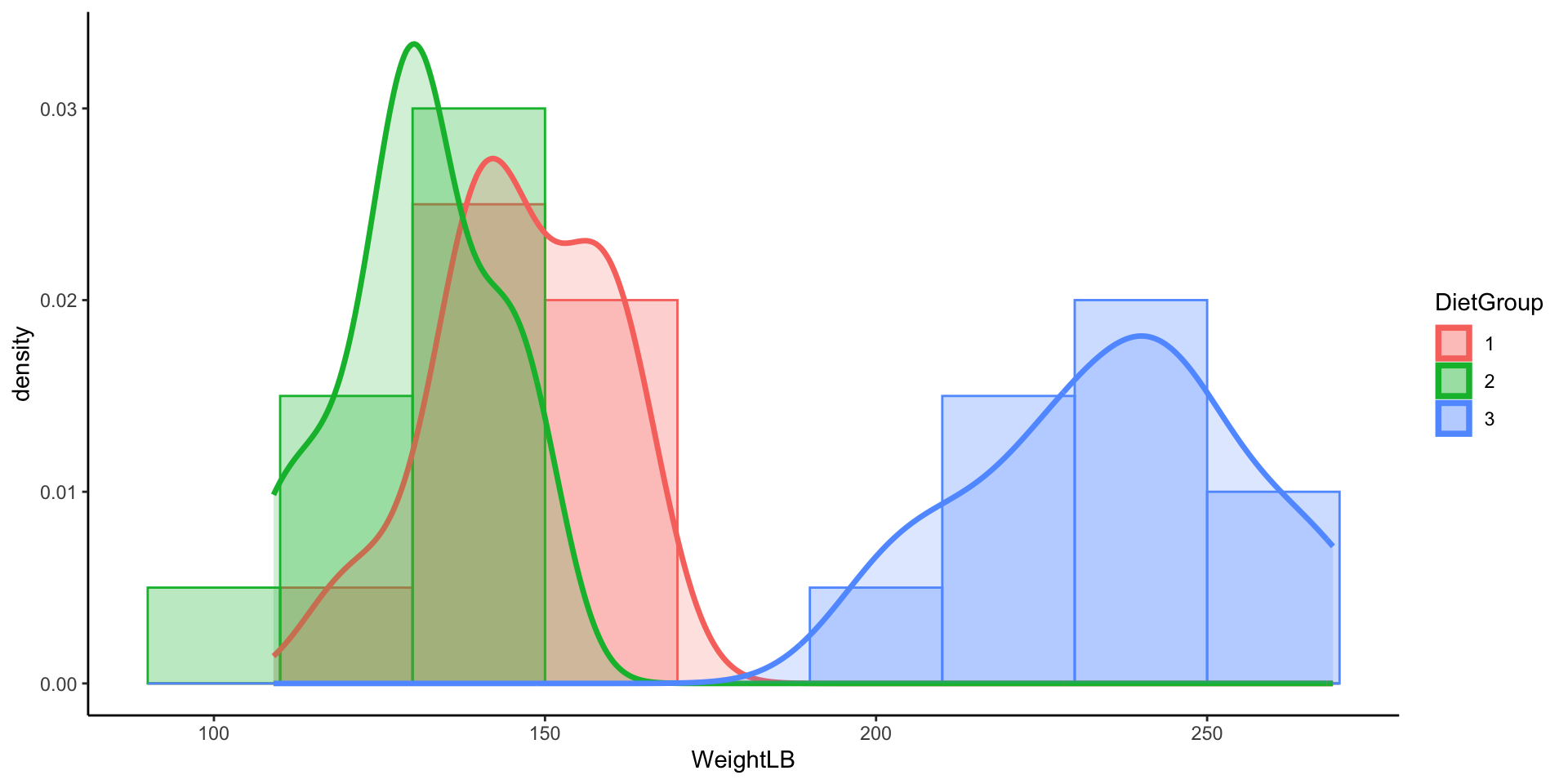
  2. DietGroup: 1, 2, 3 representing the group to which a respondent was assigned
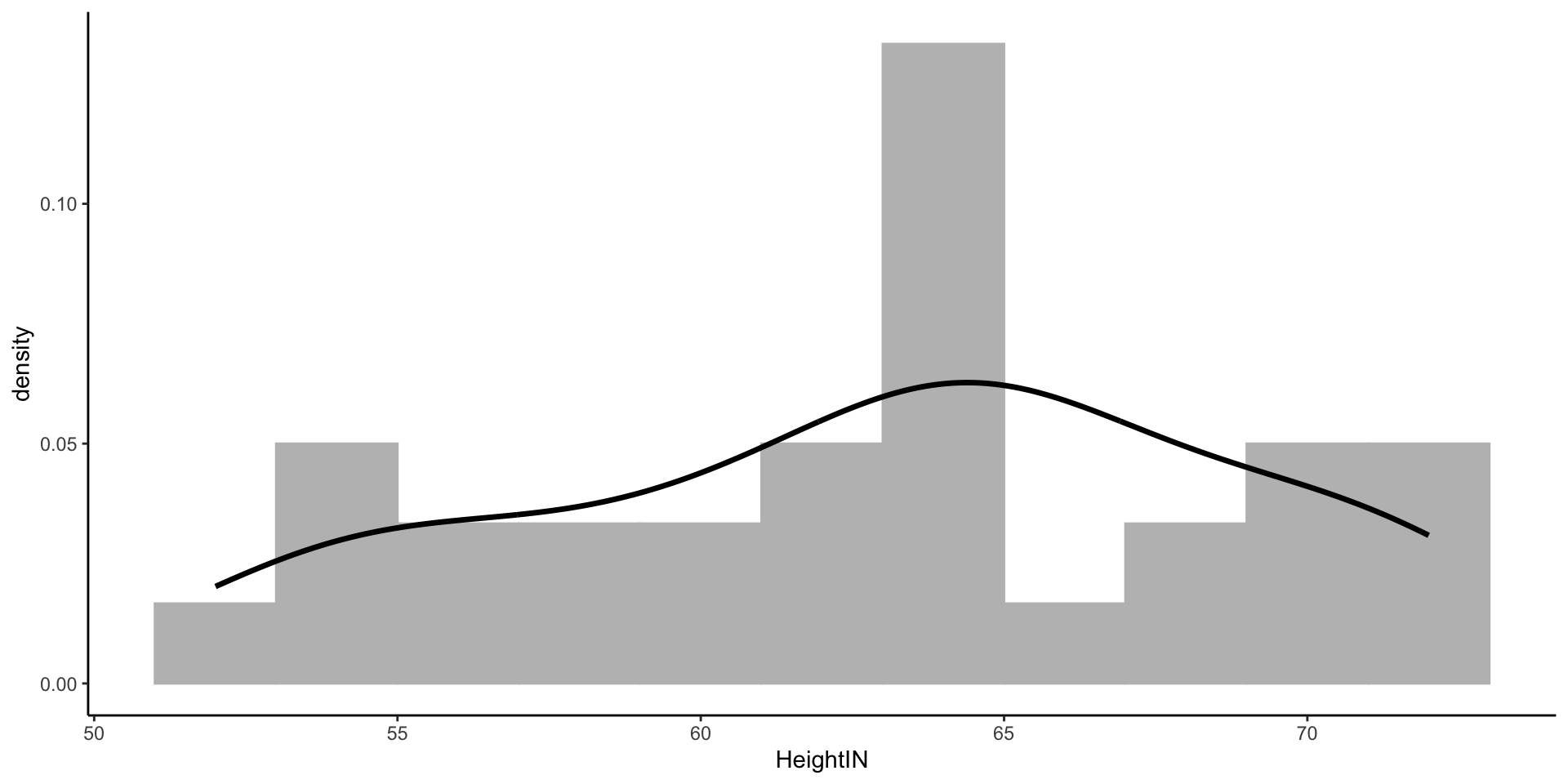
  3. HeightIN: The respondents’ height in inches
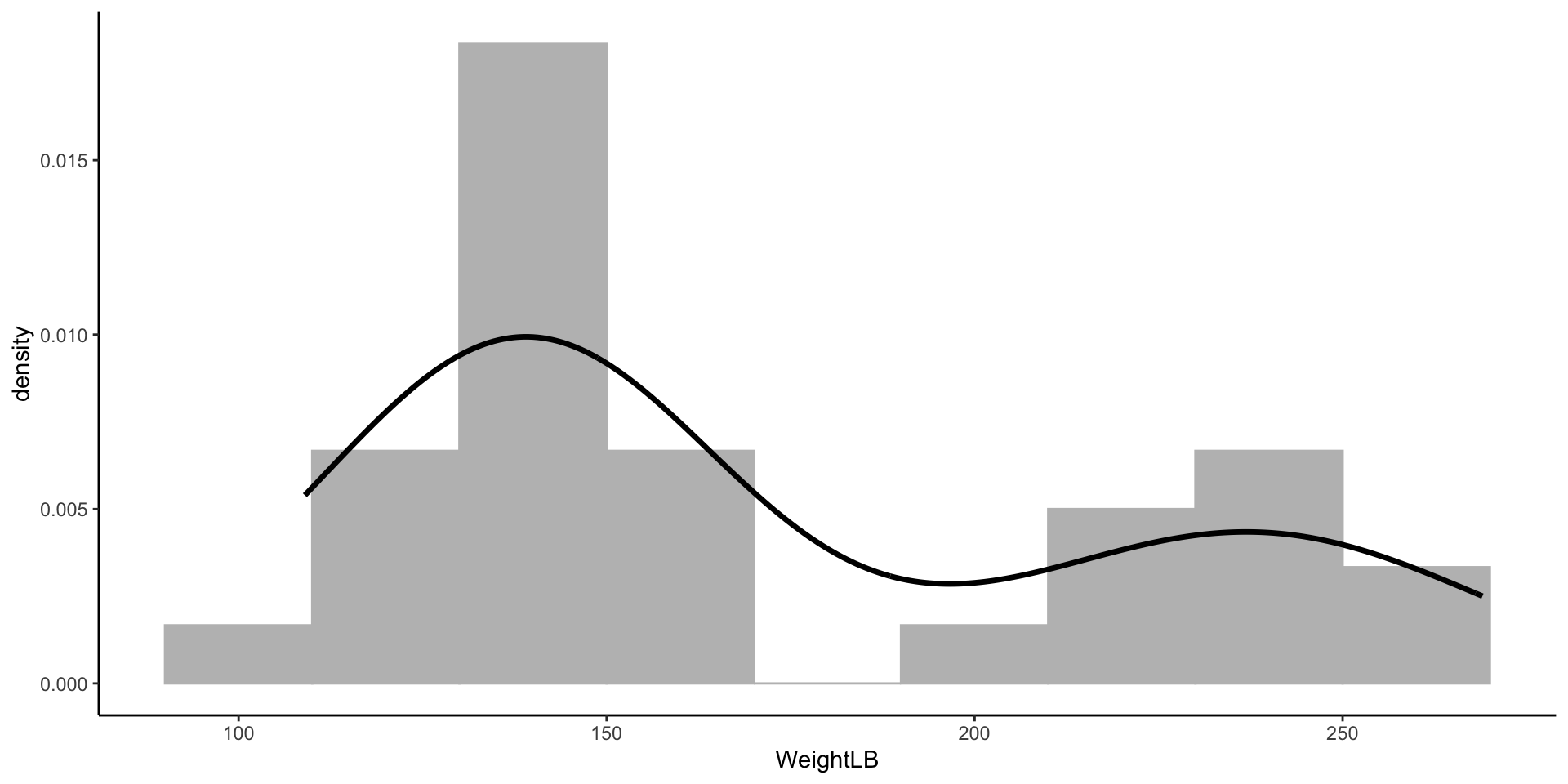
  4. WeightLB (Dependent Variable): The respondents’ weight in pounds
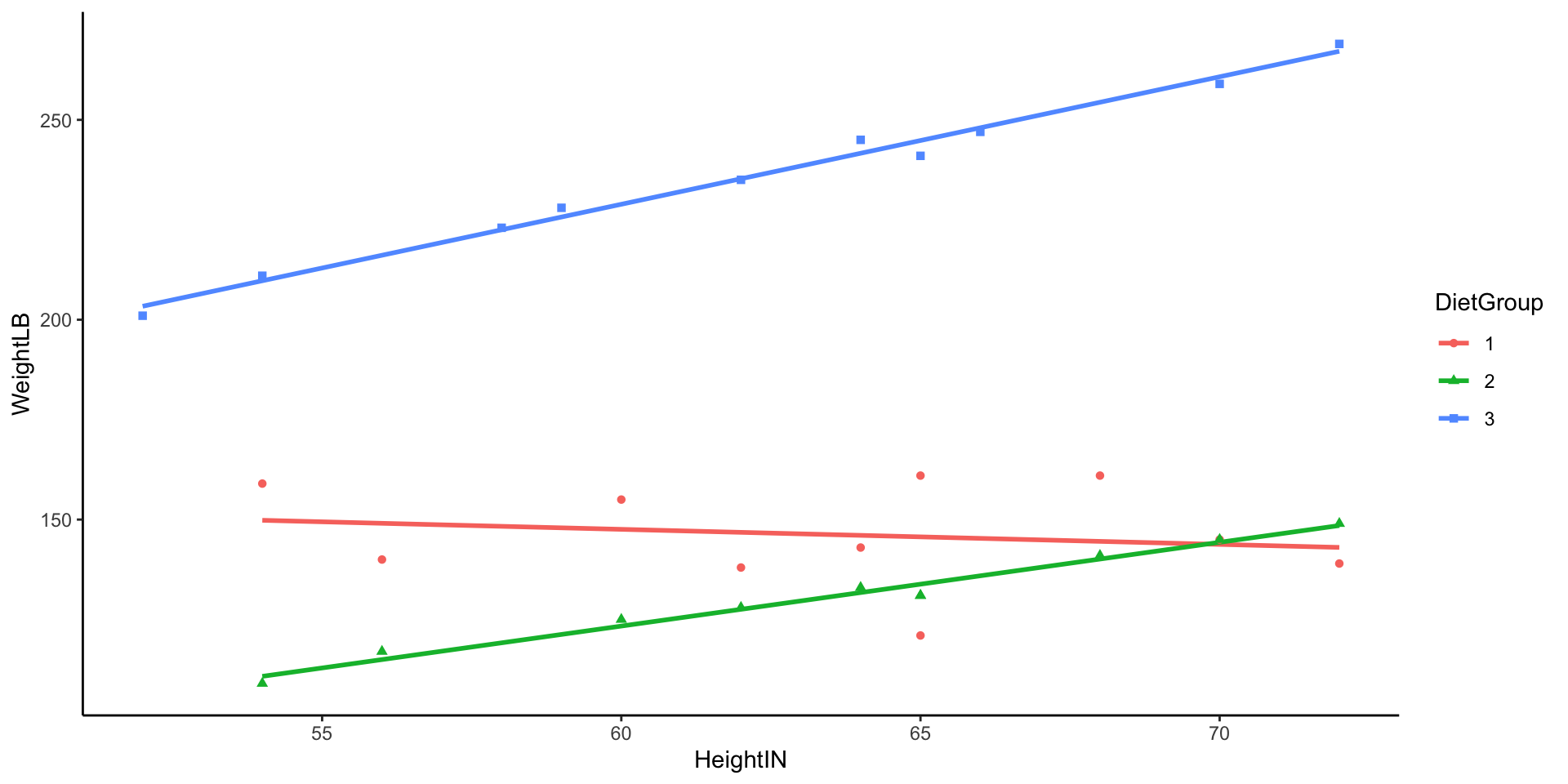
• Research Question: Are there differences in final weights between the three diet groups, and, if so, what the nature of the differences?
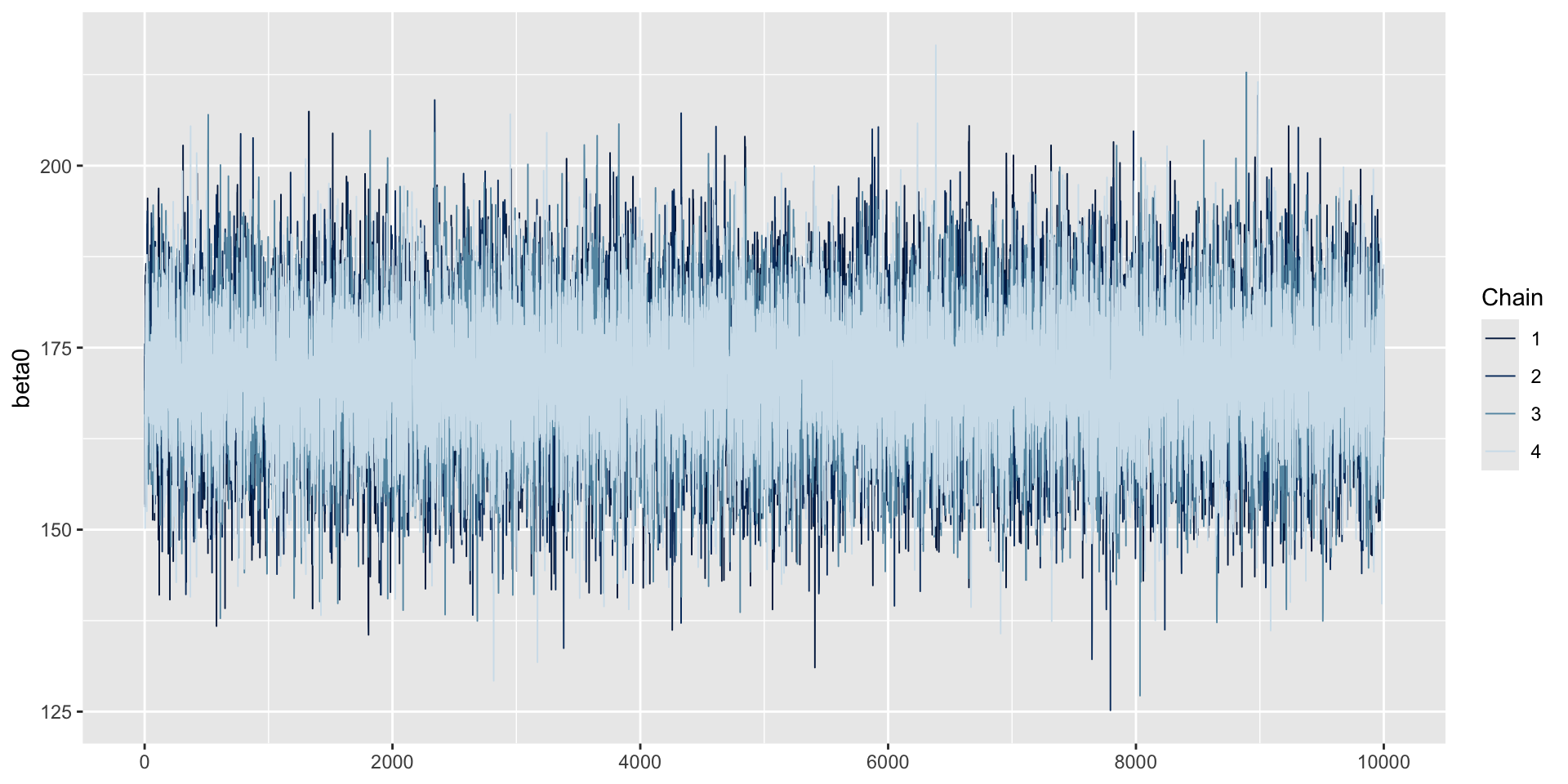
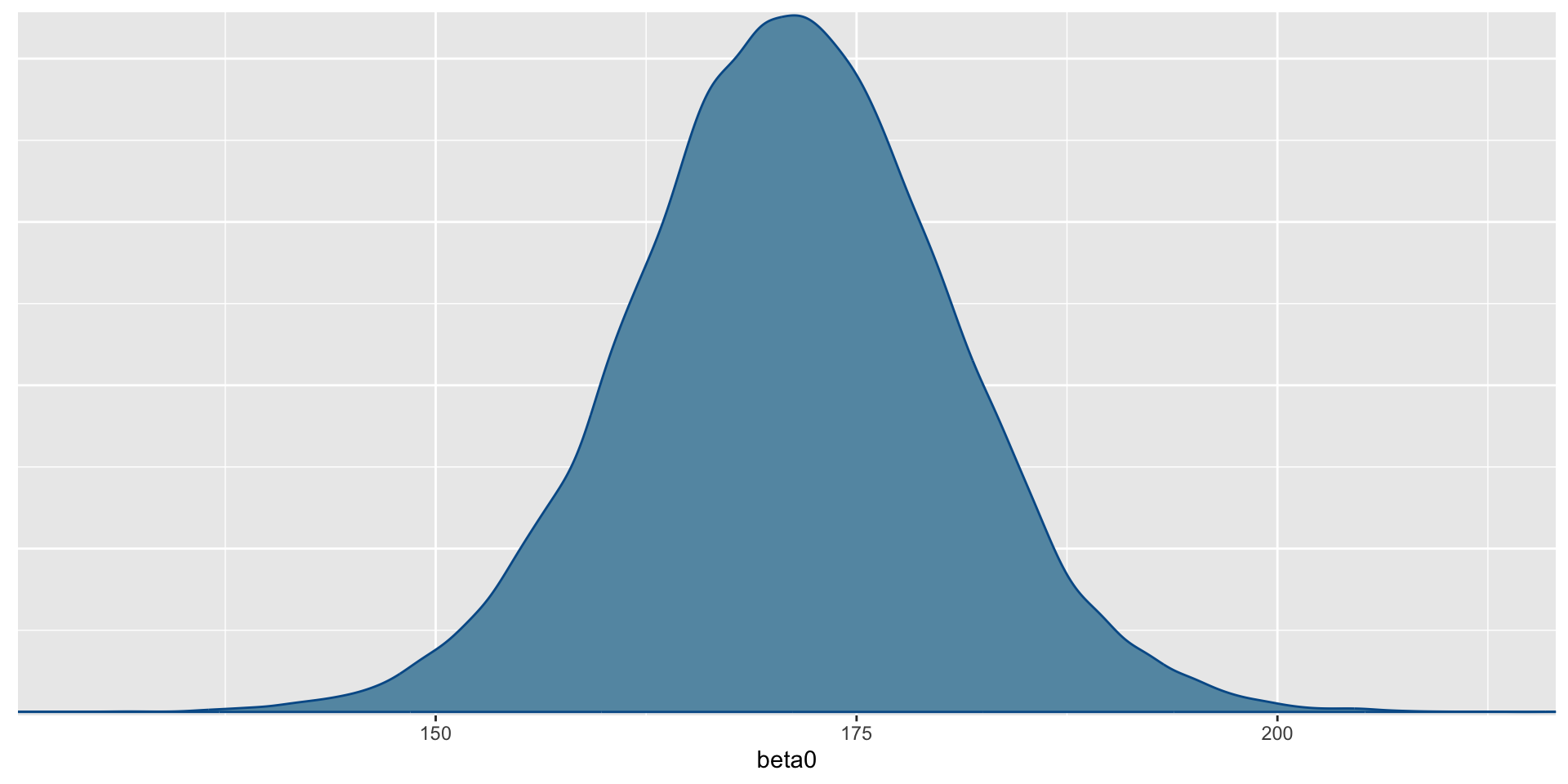
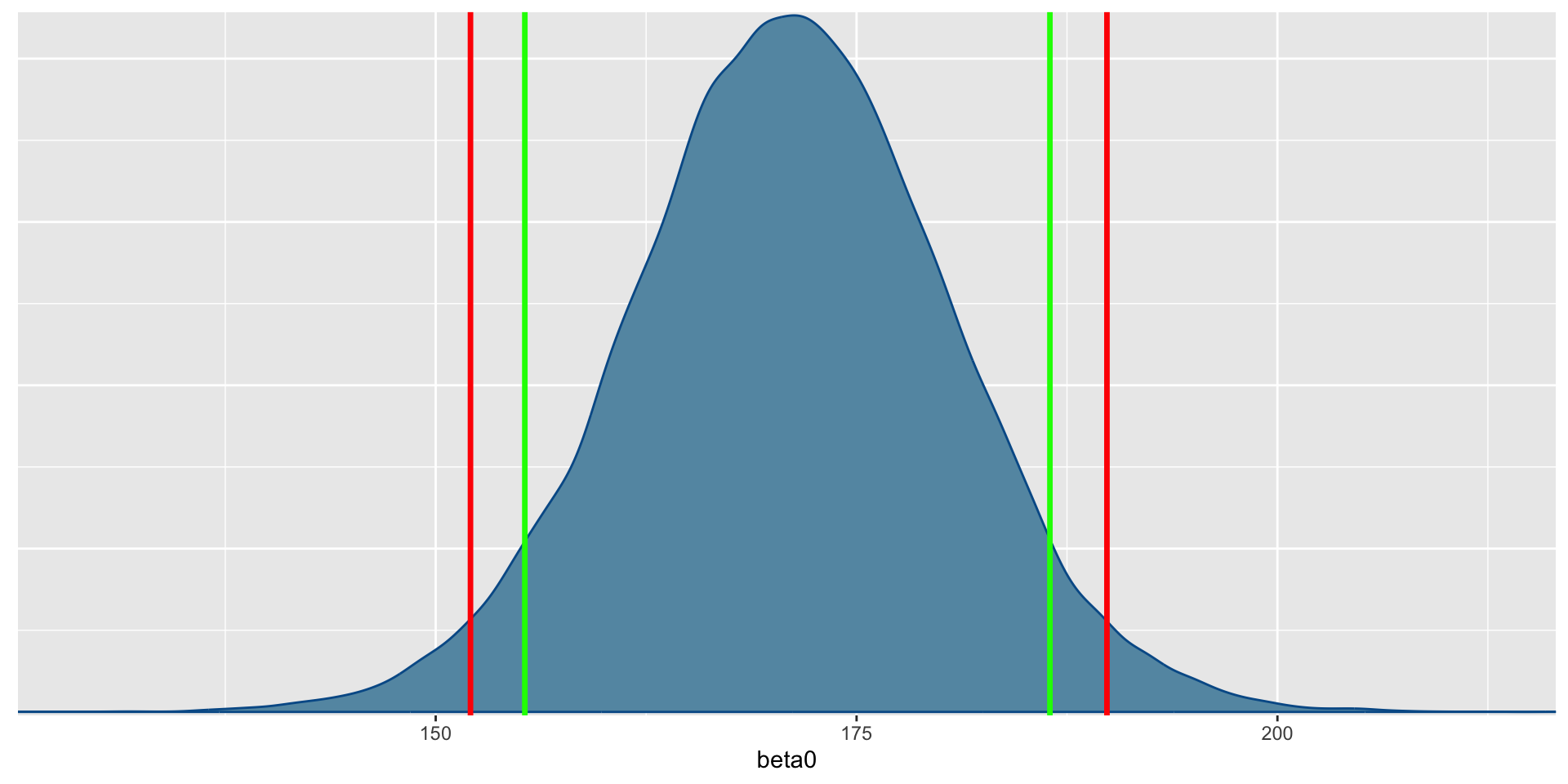
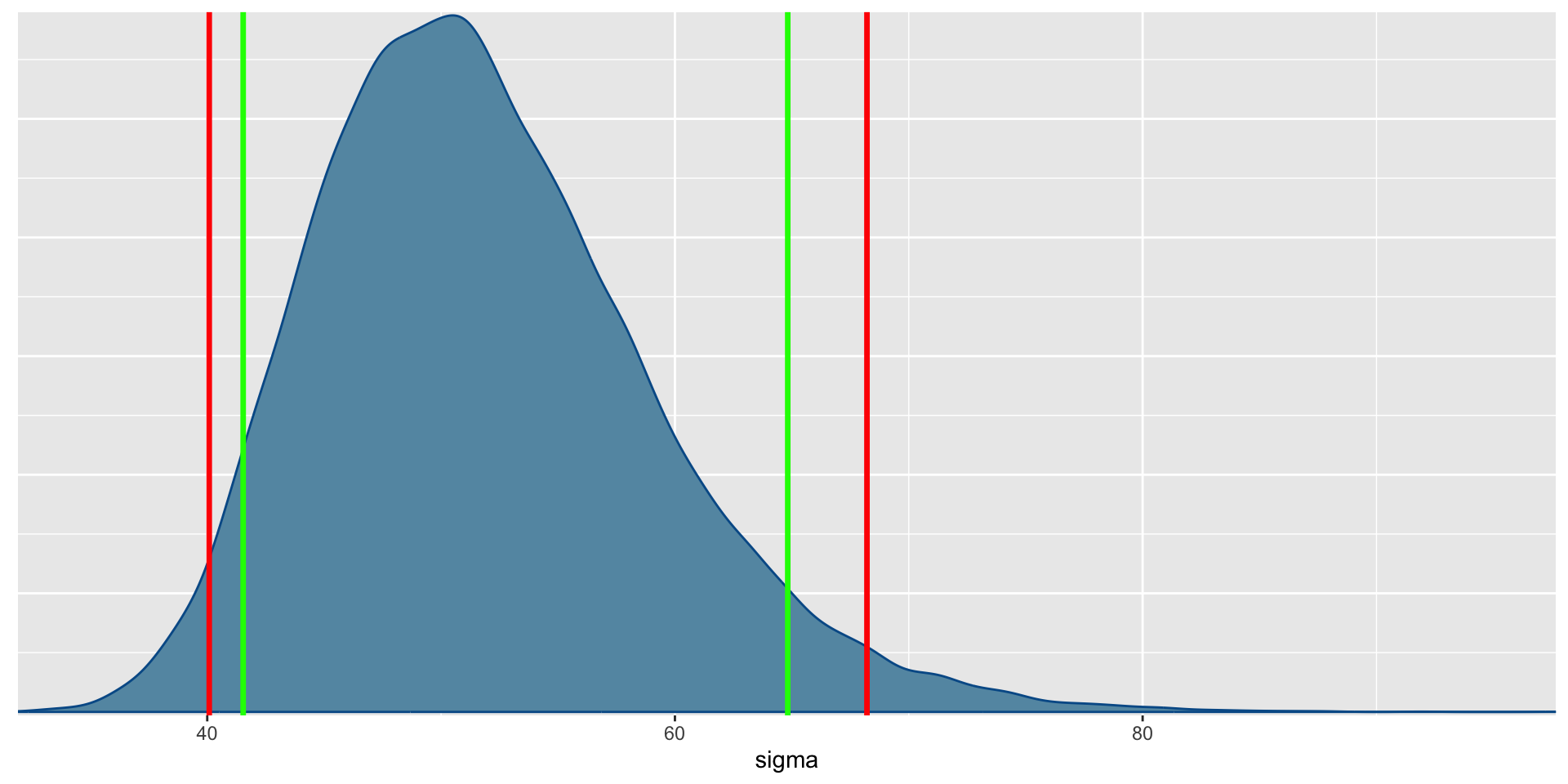
• Before we conduct the analysis, let’s look at the data

Visualizing Data: WeightLB variable

library(ggplot2) # R package for data visualization
# read in data
dat <- read.csv(here::here('posts', 'Lectures','2024-01-12-syllabus-adv-multivariate-esrm-6553', 'Lecture03', 'Code', 'DietData.csv'))
dat$DietGroup <- factor(dat$DietGroup, levels = 1:3)
head(dat)

  Respondent DietGroup HeightIN WeightLB
1          1         1       56      140
2          2         1       60      155
3          3         1       64      143
4          4         1       68      161
5          5         1       72      139
6          6         1       54      159

# Histplot for WeightLB - Dependent Variable
ggplot(dat) +
  geom_histogram(aes(x = WeightLB, y = ..density..), position = "identity", binwidth = 20, fill = 'grey', col = 'grey') +
  geom_density(aes(x = WeightLB), alpha = .2, size = 1.2) +
  theme_classic()

Visualize Data: HeightIN Variable

# Histgram for HeightIN - Independent Variable
ggplot(dat) +
  geom_histogram(aes(x = HeightIN, y = ..density..), position = "identity", binwidth = 2, fill = 'grey', col = 'grey') +
  geom_density(aes(x = HeightIN), alpha = .2, size = 1.2) +
  theme_classic()

Visualize Data: WeightLB by DietGroup

# Histgram for WeightLB x Group
ggplot(dat, aes(x = WeightLB, fill = DietGroup, col = DietGroup)) +
  geom_histogram(aes(y = ..density..), position = "identity", binwidth = 20, alpha = 0.3) +
  geom_density(alpha = .2, size = 1.2) +
  theme_classic()

Visualizing Data: WeightLB by HeightIN by DietGroup

# Histgram for WeightLB x HeightIN x Group
ggplot(dat, aes(y = WeightLB, x = HeightIN, col = DietGroup, shape = DietGroup)) +
  geom_smooth(method = 'lm', se = FALSE) +
  geom_point() +
  theme_classic()

Class Discussion: What do we do?

Now, your turn to answer (statistical) questions:

1. What type of analysis seems most appropriate for these data?
2. Is the dependent variable (WeightLB) is appropriate as-is for such analysis or does it need transformed?
3. Are the independent variables (HeightIN, DietGroup) is appropriate as-is for such analysis or does it need transformed?

Scientific Judgement…

Linear Model with Stan

# Linear Model with Least Squares
## Center independent variable - HeightIN for better interpretation
dat$HeightIN <- dat$HeightIN - 60

## an empty model suggested by data
EmptyModel <- lm(WeightLB ~ 1, data = dat)

## Examine assumptions and leverage of fit
### Residual plot, Q-Q residuals, Scale-Location
# plot(EmptyModel)

## Look at ANOVA table
### F-values, Sum/Mean of square of residuals
# anova(EmptyModel)

## look at parameter summary
summary(EmptyModel)

Call:
lm(formula = WeightLB ~ 1, data = dat)

Residuals:
   Min     1Q Median     3Q    Max 
-62.00 -36.75 -24.00  49.00  98.00 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  171.000      9.041   18.91   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 49.52 on 29 degrees of freedom

model.matrix(EmptyModel)

   (Intercept)
1            1
2            1
3            1
4            1
5            1
6            1
7            1
8            1
9            1
10           1
11           1
12           1
13           1
14           1
15           1
16           1
17           1
18           1
19           1
20           1
21           1
22           1
23           1
24           1
25           1
26           1
27           1
28           1
29           1
30           1
attr(,"assign")
[1] 0

Path Diagram of the Full Model

flowchart LR
  id1[(Empty Model)] ====> id2[(Full Model)]

Full model includes all effects (main effects, interaction effect):

1. What each arrow means? how to interpret them?
2. Can the three interaction term be included in the model? why?

graph LR;
  HeightIN60 --> WeightLB;
  DietGroup2 --> WeightLB;
  DietGroup3 --> WeightLB;
  HeightIN60xDietGroup2 --> WeightLB;
  HeightIN60xDietGroup3 --> WeightLB;
  HeightIN60xDietGroup2xDietGroup3 x-.-x WeightLB;

Steps in an MCMC Analysis

1. Model Building:

   • Specify the model

   • Specify prior distribution for all parameters

   • Build model syntax as needed

2. Model Estimation:

   • Specify warmup/burnin and sampling period lengths

   • Run Markov chains

3. Model Evaluation:

   • Evaluate chain convergence

   • Interpret/report results

Specified the Model

• To begin, let’s start with an empty model and build up from there

• Let’s examine the linear model we seek to estimate:

  \[ \text{WeightLB}_i = \beta_0 + e_i \]

  Where: \(e_i \sim N(0, \sigma^2_{e})\)

• Questions here:

  • What are the variables in this analysis?

  • What are the parameters in this analysis?

Introduction to Stan

• Stan is an MCMC estimation program

  • Most recent; has many convenient features

  • Actually does several methods of estimation (ML, Variational Bayes)

• You create a model using Stan’s syntax

  • Stan translates your model to a custom-built C++ syntax

  • Stan then compiles your model into its own executable program

• You then run the program to estimate your model

  • If you use R, the interface can be seamless

Stan and Rstudio

• Option 1: Stan has its own syntax which can be built in stand-alone text files (.stan)

  • Rstudio will let you create a stan file in the new File menu

  • Rstudio also has syntax highlighting in Stan files

  • Save .stan to the same path of your .r

• Option 2: You can also use Stan in a interactive way in qmd file

  • Which is helpful when you want to test multiple stan models and report your results at the same time

Create a new Stan file in Rstudio

Stan and R code blocks in qmd file

Stan Syntax

A Stan file saved as EmptyModel.stan

• Each line ends with a semi colon ;
• Comments are put in with //
• Each block starts with block type and is surrounded by curly brackets {}

EmptyModel.stan

data {  //
  int<lower=0> N; //
  vector[N] y; //
}
parameters { //
  real beta0; //
  real<lower=0> sigma; //
}
model { //
  beta0 ~ normal(0, 1000); //
  sigma ~ uniform(0, 100000); //
  y ~ normal(beta0, sigma); //
}

1

the data block include the observed information

2

sample size (declared as a integer value)

3

dependent variable (declared as vector with the length as sample size)

4

the parameter block includes all parameters we want to estimate

5

intercept parameter

6

standard deviation of residuals

7

the model block includes the prior information and likelihood

8

prior distribution for beta_0

9

prior distribution for SD of residuals

10

likelihood function for observed data

Stan Data and Parameter Declaration

EmptyModel.stan

data {
  int<lower=0> N; 
  vector[N] y; 
}

• Like many compiled languages (e.g., Java, C++), Stan expects you to declare what types of data/parameters you are defining:

  • int: Integer values (no decimals)

  • real: Floating point numbers

  • vector: A one-dimensional set of real valued numbers

• Sometimes, additional definitions are provided giving the range of the variable (or restricting the set of starting values):

  • See here for more information about data types in Stan.

  • real<lower=0> sigma ;

• For vector or matrix or array , we may need to add size to tell Stan how many elements it has.

  • vector[N] has N elements

Stan Data and Prior Distributions

EmptyModel.stan

model {
  beta0 ~ normal(0, 1000);
  sigma ~ uniform(0, 100000);
  y ~ normal(beta0, sigma);
}

• In the model block, we need to define the prior distribution for the model and the priors

  • The left-hand side is either defined in data or parameters

  • The right-hand side is a distribution included in Stan

    • You can define your own distribution (see here for more information)
• If you have hyperparameters, you can consider them as same as parameters

EmptyModel.stan

data {
  ...
  real<lower=0> betaSigma;
  real<lower=0> sigmaMax;
}
model {
  beta0 ~ normal(0, betaSigma);
  sigma ~ uniform(0, sigmaMax);
  ...
}

1

You provide Stan with the SD of intercept

2

You provide Stan with the maximum of sigma

From Stan Syntax to Compilation

DietDataExample.R

# compile model -- this method is for stand-alone stan files (uses cmdstanr)
#setwd("~/Documents/Projects/quarto-academic-jihong/posts/2024-01-12-syllabus-adv-multivariate-esrm-6553/Lecture03")
model00.fromFile = cmdstan_model(stan_file = "Code/EmptyModel.stan")

# or this method using the string text in R
stanModel <- "
data {
  int<lower=0> N;
  vector[N] y;
}
parameters {
  real beta0;
  real<lower=0> sigma;
}
model {
  beta0 ~ normal(0, 1000);
  sigma ~ uniform(0, 100000);
  y ~ normal(beta0, sigma);
}
"
model00.fromString = cmdstan_model(stan_file = write_stan_file(stanModel))

1

stanModel is a character containing the entire Stan program

• Once you have your syntax, next you need to have Stan translate it into C++ and compile an executable. The default argument compile = TRUE make a executable file EmptyModel for you.

CmdStanModel Object

DietDataExample.R

names(model00.fromString)

1

model00.fromString is a R6 class object. All functions towards this object are stored inside itself.

 [1] ".__enclos_env__"     "functions"           "expose_functions"   
 [4] "diagnose"            "generate_quantities" "pathfinder"         
 [7] "variational"         "laplace"             "optimize"           
[10] "sample_mpi"          "sample"              "format"             
[13] "check_syntax"        "variables"           "compile"            
[16] "clone"               "save_hpp_file"       "hpp_file"           
[19] "cpp_options"         "exe_file"            "model_name"         
[22] "has_stan_file"       "stan_file"           "print"              
[25] "code"                "include_paths"       "initialize"         

• Some important functions include $sample() or $diagnose()
• cmdstanr wants you to compile first, then run the Markov chain
• Check here for more details of functions.

Building Data for Stan

DietDataExample.R

# build R list containing data for Stan: Must be named what "data" are listed in analysis
stanData = list(
  N = nrow(dat),
  weightLB = dat$WeightLB
)

1

Sample size, nrow() calculates the number of rows of data

2

Vector of dependent variable

• Stan needs the data you declared in you syntax to be able to run

• Within R, we can pass this data list to Stan via a list object

• The entries in the list should correspond to the data block of the Stan syntax

• The R list object is the same for cmdstanr and rstan

Run Markov Chains in CmdStanr

DietDataExample.R

# run MCMC chain (sample from posterior)
model00.samples = model00.fromFile$sample(
  data = stanData,
  seed = 1,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 10000,
  iter_sampling = 10000
)

1

Data list

2

Random number seed

3

Number of chains (and parallel chains)

4

Number of warmup iterations (more details shirtly)

5

Number of sampling iterations

Running MCMC with 4 parallel chains...

Chain 1 Iteration:     1 / 20000 [  0%]  (Warmup) 
Chain 1 Iteration:   100 / 20000 [  0%]  (Warmup) 
Chain 1 Iteration:   200 / 20000 [  1%]  (Warmup) 
Chain 1 Iteration:   300 / 20000 [  1%]  (Warmup) 
Chain 1 Iteration:   400 / 20000 [  2%]  (Warmup) 
Chain 1 Iteration:   500 / 20000 [  2%]  (Warmup) 
Chain 1 Iteration:   600 / 20000 [  3%]  (Warmup) 
Chain 1 Iteration:   700 / 20000 [  3%]  (Warmup) 
Chain 1 Iteration:   800 / 20000 [  4%]  (Warmup) 
Chain 1 Iteration:   900 / 20000 [  4%]  (Warmup) 
Chain 1 Iteration:  1000 / 20000 [  5%]  (Warmup) 
Chain 1 Iteration:  1100 / 20000 [  5%]  (Warmup) 
Chain 1 Iteration:  1200 / 20000 [  6%]  (Warmup) 
Chain 1 Iteration:  1300 / 20000 [  6%]  (Warmup) 
Chain 1 Iteration:  1400 / 20000 [  7%]  (Warmup) 
Chain 1 Iteration:  1500 / 20000 [  7%]  (Warmup) 
Chain 1 Iteration:  1600 / 20000 [  8%]  (Warmup) 
Chain 1 Iteration:  1700 / 20000 [  8%]  (Warmup) 
Chain 1 Iteration:  1800 / 20000 [  9%]  (Warmup) 
Chain 1 Iteration:  1900 / 20000 [  9%]  (Warmup) 
Chain 1 Iteration:  2000 / 20000 [ 10%]  (Warmup) 
Chain 1 Iteration:  2100 / 20000 [ 10%]  (Warmup) 
Chain 1 Iteration:  2200 / 20000 [ 11%]  (Warmup) 
Chain 1 Iteration:  2300 / 20000 [ 11%]  (Warmup) 
Chain 1 Iteration:  2400 / 20000 [ 12%]  (Warmup) 
Chain 1 Iteration:  2500 / 20000 [ 12%]  (Warmup) 
Chain 1 Iteration:  2600 / 20000 [ 13%]  (Warmup) 
Chain 1 Iteration:  2700 / 20000 [ 13%]  (Warmup) 
Chain 1 Iteration:  2800 / 20000 [ 14%]  (Warmup) 
Chain 1 Iteration:  2900 / 20000 [ 14%]  (Warmup) 
Chain 1 Iteration:  3000 / 20000 [ 15%]  (Warmup) 
Chain 1 Iteration:  3100 / 20000 [ 15%]  (Warmup) 
Chain 1 Iteration:  3200 / 20000 [ 16%]  (Warmup) 
Chain 1 Iteration:  3300 / 20000 [ 16%]  (Warmup) 
Chain 1 Iteration:  3400 / 20000 [ 17%]  (Warmup) 
Chain 1 Iteration:  3500 / 20000 [ 17%]  (Warmup) 
Chain 1 Iteration:  3600 / 20000 [ 18%]  (Warmup) 
Chain 1 Iteration:  3700 / 20000 [ 18%]  (Warmup) 
Chain 1 Iteration:  3800 / 20000 [ 19%]  (Warmup) 
Chain 1 Iteration:  3900 / 20000 [ 19%]  (Warmup) 
Chain 1 Iteration:  4000 / 20000 [ 20%]  (Warmup) 
Chain 1 Iteration:  4100 / 20000 [ 20%]  (Warmup) 
Chain 1 Iteration:  4200 / 20000 [ 21%]  (Warmup) 
Chain 1 Iteration:  4300 / 20000 [ 21%]  (Warmup) 
Chain 1 Iteration:  4400 / 20000 [ 22%]  (Warmup) 
Chain 1 Iteration:  4500 / 20000 [ 22%]  (Warmup) 
Chain 1 Iteration:  4600 / 20000 [ 23%]  (Warmup) 
Chain 1 Iteration:  4700 / 20000 [ 23%]  (Warmup) 
Chain 1 Iteration:  4800 / 20000 [ 24%]  (Warmup) 
Chain 1 Iteration:  4900 / 20000 [ 24%]  (Warmup) 
Chain 1 Iteration:  5000 / 20000 [ 25%]  (Warmup) 
Chain 1 Iteration:  5100 / 20000 [ 25%]  (Warmup) 
Chain 1 Iteration:  5200 / 20000 [ 26%]  (Warmup) 
Chain 1 Iteration:  5300 / 20000 [ 26%]  (Warmup) 
Chain 1 Iteration:  5400 / 20000 [ 27%]  (Warmup) 
Chain 1 Iteration:  5500 / 20000 [ 27%]  (Warmup) 
Chain 1 Iteration:  5600 / 20000 [ 28%]  (Warmup) 
Chain 1 Iteration:  5700 / 20000 [ 28%]  (Warmup) 
Chain 1 Iteration:  5800 / 20000 [ 29%]  (Warmup) 
Chain 1 Iteration:  5900 / 20000 [ 29%]  (Warmup) 
Chain 1 Iteration:  6000 / 20000 [ 30%]  (Warmup) 
Chain 1 Iteration:  6100 / 20000 [ 30%]  (Warmup) 
Chain 1 Iteration:  6200 / 20000 [ 31%]  (Warmup) 
Chain 1 Iteration:  6300 / 20000 [ 31%]  (Warmup) 
Chain 1 Iteration:  6400 / 20000 [ 32%]  (Warmup) 
Chain 1 Iteration:  6500 / 20000 [ 32%]  (Warmup) 
Chain 1 Iteration:  6600 / 20000 [ 33%]  (Warmup) 
Chain 1 Iteration:  6700 / 20000 [ 33%]  (Warmup) 
Chain 1 Iteration:  6800 / 20000 [ 34%]  (Warmup) 
Chain 1 Iteration:  6900 / 20000 [ 34%]  (Warmup) 
Chain 1 Iteration:  7000 / 20000 [ 35%]  (Warmup) 
Chain 1 Iteration:  7100 / 20000 [ 35%]  (Warmup) 
Chain 1 Iteration:  7200 / 20000 [ 36%]  (Warmup) 
Chain 1 Iteration:  7300 / 20000 [ 36%]  (Warmup) 
Chain 1 Iteration:  7400 / 20000 [ 37%]  (Warmup) 
Chain 1 Iteration:  7500 / 20000 [ 37%]  (Warmup) 
Chain 1 Iteration:  7600 / 20000 [ 38%]  (Warmup) 
Chain 1 Iteration:  7700 / 20000 [ 38%]  (Warmup) 
Chain 1 Iteration:  7800 / 20000 [ 39%]  (Warmup) 
Chain 1 Iteration:  7900 / 20000 [ 39%]  (Warmup) 
Chain 1 Iteration:  8000 / 20000 [ 40%]  (Warmup) 
Chain 1 Iteration:  8100 / 20000 [ 40%]  (Warmup) 
Chain 1 Iteration:  8200 / 20000 [ 41%]  (Warmup) 
Chain 1 Iteration:  8300 / 20000 [ 41%]  (Warmup) 
Chain 1 Iteration:  8400 / 20000 [ 42%]  (Warmup) 
Chain 1 Iteration:  8500 / 20000 [ 42%]  (Warmup) 
Chain 1 Iteration:  8600 / 20000 [ 43%]  (Warmup) 
Chain 1 Iteration:  8700 / 20000 [ 43%]  (Warmup) 
Chain 1 Iteration:  8800 / 20000 [ 44%]  (Warmup) 
Chain 1 Iteration:  8900 / 20000 [ 44%]  (Warmup) 
Chain 1 Iteration:  9000 / 20000 [ 45%]  (Warmup) 
Chain 1 Iteration:  9100 / 20000 [ 45%]  (Warmup) 
Chain 1 Iteration:  9200 / 20000 [ 46%]  (Warmup) 
Chain 1 Iteration:  9300 / 20000 [ 46%]  (Warmup) 
Chain 1 Iteration:  9400 / 20000 [ 47%]  (Warmup) 
Chain 1 Iteration:  9500 / 20000 [ 47%]  (Warmup) 
Chain 1 Iteration:  9600 / 20000 [ 48%]  (Warmup) 
Chain 1 Iteration:  9700 / 20000 [ 48%]  (Warmup) 
Chain 1 Iteration:  9800 / 20000 [ 49%]  (Warmup) 
Chain 1 Iteration:  9900 / 20000 [ 49%]  (Warmup) 
Chain 1 Iteration: 10000 / 20000 [ 50%]  (Warmup) 
Chain 1 Iteration: 10001 / 20000 [ 50%]  (Sampling) 
Chain 1 Iteration: 10100 / 20000 [ 50%]  (Sampling) 
Chain 1 Iteration: 10200 / 20000 [ 51%]  (Sampling) 
Chain 1 Iteration: 10300 / 20000 [ 51%]  (Sampling) 
Chain 1 Iteration: 10400 / 20000 [ 52%]  (Sampling) 
Chain 1 Iteration: 10500 / 20000 [ 52%]  (Sampling) 
Chain 1 Iteration: 10600 / 20000 [ 53%]  (Sampling) 
Chain 1 Iteration: 10700 / 20000 [ 53%]  (Sampling) 
Chain 1 Iteration: 10800 / 20000 [ 54%]  (Sampling) 
Chain 1 Iteration: 10900 / 20000 [ 54%]  (Sampling) 
Chain 1 Iteration: 11000 / 20000 [ 55%]  (Sampling) 
Chain 1 Iteration: 11100 / 20000 [ 55%]  (Sampling) 
Chain 1 Iteration: 11200 / 20000 [ 56%]  (Sampling) 
Chain 1 Iteration: 11300 / 20000 [ 56%]  (Sampling) 
Chain 1 Iteration: 11400 / 20000 [ 57%]  (Sampling) 
Chain 1 Iteration: 11500 / 20000 [ 57%]  (Sampling) 
Chain 1 Iteration: 11600 / 20000 [ 58%]  (Sampling) 
Chain 1 Iteration: 11700 / 20000 [ 58%]  (Sampling) 
Chain 1 Iteration: 11800 / 20000 [ 59%]  (Sampling) 
Chain 1 Iteration: 11900 / 20000 [ 59%]  (Sampling) 
Chain 1 Iteration: 12000 / 20000 [ 60%]  (Sampling) 
Chain 1 Iteration: 12100 / 20000 [ 60%]  (Sampling) 
Chain 1 Iteration: 12200 / 20000 [ 61%]  (Sampling) 
Chain 1 Iteration: 12300 / 20000 [ 61%]  (Sampling) 
Chain 1 Iteration: 12400 / 20000 [ 62%]  (Sampling) 
Chain 1 Iteration: 12500 / 20000 [ 62%]  (Sampling) 
Chain 1 Iteration: 12600 / 20000 [ 63%]  (Sampling) 
Chain 1 Iteration: 12700 / 20000 [ 63%]  (Sampling) 
Chain 1 Iteration: 12800 / 20000 [ 64%]  (Sampling) 
Chain 1 Iteration: 12900 / 20000 [ 64%]  (Sampling) 
Chain 1 Iteration: 13000 / 20000 [ 65%]  (Sampling) 
Chain 1 Iteration: 13100 / 20000 [ 65%]  (Sampling) 
Chain 1 Iteration: 13200 / 20000 [ 66%]  (Sampling) 
Chain 1 Iteration: 13300 / 20000 [ 66%]  (Sampling) 
Chain 1 Iteration: 13400 / 20000 [ 67%]  (Sampling) 
Chain 1 Iteration: 13500 / 20000 [ 67%]  (Sampling) 
Chain 1 Iteration: 13600 / 20000 [ 68%]  (Sampling) 
Chain 2 Iteration:     1 / 20000 [  0%]  (Warmup) 
Chain 2 Iteration:   100 / 20000 [  0%]  (Warmup) 
Chain 2 Iteration:   200 / 20000 [  1%]  (Warmup) 
Chain 2 Iteration:   300 / 20000 [  1%]  (Warmup) 
Chain 2 Iteration:   400 / 20000 [  2%]  (Warmup) 
Chain 2 Iteration:   500 / 20000 [  2%]  (Warmup) 
Chain 2 Iteration:   600 / 20000 [  3%]  (Warmup) 
Chain 2 Iteration:   700 / 20000 [  3%]  (Warmup) 
Chain 2 Iteration:   800 / 20000 [  4%]  (Warmup) 
Chain 2 Iteration:   900 / 20000 [  4%]  (Warmup) 
Chain 2 Iteration:  1000 / 20000 [  5%]  (Warmup) 
Chain 2 Iteration:  1100 / 20000 [  5%]  (Warmup) 
Chain 2 Iteration:  1200 / 20000 [  6%]  (Warmup) 
Chain 2 Iteration:  1300 / 20000 [  6%]  (Warmup) 
Chain 2 Iteration:  1400 / 20000 [  7%]  (Warmup) 
Chain 2 Iteration:  1500 / 20000 [  7%]  (Warmup) 
Chain 2 Iteration:  1600 / 20000 [  8%]  (Warmup) 
Chain 2 Iteration:  1700 / 20000 [  8%]  (Warmup) 
Chain 2 Iteration:  1800 / 20000 [  9%]  (Warmup) 
Chain 2 Iteration:  1900 / 20000 [  9%]  (Warmup) 
Chain 2 Iteration:  2000 / 20000 [ 10%]  (Warmup) 
Chain 2 Iteration:  2100 / 20000 [ 10%]  (Warmup) 
Chain 2 Iteration:  2200 / 20000 [ 11%]  (Warmup) 
Chain 2 Iteration:  2300 / 20000 [ 11%]  (Warmup) 
Chain 2 Iteration:  2400 / 20000 [ 12%]  (Warmup) 
Chain 2 Iteration:  2500 / 20000 [ 12%]  (Warmup) 
Chain 2 Iteration:  2600 / 20000 [ 13%]  (Warmup) 
Chain 2 Iteration:  2700 / 20000 [ 13%]  (Warmup) 
Chain 2 Iteration:  2800 / 20000 [ 14%]  (Warmup) 
Chain 2 Iteration:  2900 / 20000 [ 14%]  (Warmup) 
Chain 2 Iteration:  3000 / 20000 [ 15%]  (Warmup) 
Chain 2 Iteration:  3100 / 20000 [ 15%]  (Warmup) 
Chain 2 Iteration:  3200 / 20000 [ 16%]  (Warmup) 
Chain 2 Iteration:  3300 / 20000 [ 16%]  (Warmup) 
Chain 2 Iteration:  3400 / 20000 [ 17%]  (Warmup) 
Chain 2 Iteration:  3500 / 20000 [ 17%]  (Warmup) 
Chain 2 Iteration:  3600 / 20000 [ 18%]  (Warmup) 
Chain 2 Iteration:  3700 / 20000 [ 18%]  (Warmup) 
Chain 2 Iteration:  3800 / 20000 [ 19%]  (Warmup) 
Chain 2 Iteration:  3900 / 20000 [ 19%]  (Warmup) 
Chain 2 Iteration:  4000 / 20000 [ 20%]  (Warmup) 
Chain 2 Iteration:  4100 / 20000 [ 20%]  (Warmup) 
Chain 2 Iteration:  4200 / 20000 [ 21%]  (Warmup) 
Chain 2 Iteration:  4300 / 20000 [ 21%]  (Warmup) 
Chain 2 Iteration:  4400 / 20000 [ 22%]  (Warmup) 
Chain 2 Iteration:  4500 / 20000 [ 22%]  (Warmup) 
Chain 2 Iteration:  4600 / 20000 [ 23%]  (Warmup) 
Chain 2 Iteration:  4700 / 20000 [ 23%]  (Warmup) 
Chain 2 Iteration:  4800 / 20000 [ 24%]  (Warmup) 
Chain 2 Iteration:  4900 / 20000 [ 24%]  (Warmup) 
Chain 2 Iteration:  5000 / 20000 [ 25%]  (Warmup) 
Chain 2 Iteration:  5100 / 20000 [ 25%]  (Warmup) 
Chain 2 Iteration:  5200 / 20000 [ 26%]  (Warmup) 
Chain 2 Iteration:  5300 / 20000 [ 26%]  (Warmup) 
Chain 2 Iteration:  5400 / 20000 [ 27%]  (Warmup) 
Chain 2 Iteration:  5500 / 20000 [ 27%]  (Warmup) 
Chain 2 Iteration:  5600 / 20000 [ 28%]  (Warmup) 
Chain 2 Iteration:  5700 / 20000 [ 28%]  (Warmup) 
Chain 2 Iteration:  5800 / 20000 [ 29%]  (Warmup) 
Chain 2 Iteration:  5900 / 20000 [ 29%]  (Warmup) 
Chain 2 Iteration:  6000 / 20000 [ 30%]  (Warmup) 
Chain 2 Iteration:  6100 / 20000 [ 30%]  (Warmup) 
Chain 2 Iteration:  6200 / 20000 [ 31%]  (Warmup) 
Chain 2 Iteration:  6300 / 20000 [ 31%]  (Warmup) 
Chain 2 Iteration:  6400 / 20000 [ 32%]  (Warmup) 
Chain 2 Iteration:  6500 / 20000 [ 32%]  (Warmup) 
Chain 2 Iteration:  6600 / 20000 [ 33%]  (Warmup) 
Chain 2 Iteration:  6700 / 20000 [ 33%]  (Warmup) 
Chain 2 Iteration:  6800 / 20000 [ 34%]  (Warmup) 
Chain 2 Iteration:  6900 / 20000 [ 34%]  (Warmup) 
Chain 2 Iteration:  7000 / 20000 [ 35%]  (Warmup) 
Chain 2 Iteration:  7100 / 20000 [ 35%]  (Warmup) 
Chain 2 Iteration:  7200 / 20000 [ 36%]  (Warmup) 
Chain 2 Iteration:  7300 / 20000 [ 36%]  (Warmup) 
Chain 2 Iteration:  7400 / 20000 [ 37%]  (Warmup) 
Chain 2 Iteration:  7500 / 20000 [ 37%]  (Warmup) 
Chain 2 Iteration:  7600 / 20000 [ 38%]  (Warmup) 
Chain 2 Iteration:  7700 / 20000 [ 38%]  (Warmup) 
Chain 2 Iteration:  7800 / 20000 [ 39%]  (Warmup) 
Chain 2 Iteration:  7900 / 20000 [ 39%]  (Warmup) 
Chain 2 Iteration:  8000 / 20000 [ 40%]  (Warmup) 
Chain 2 Iteration:  8100 / 20000 [ 40%]  (Warmup) 
Chain 2 Iteration:  8200 / 20000 [ 41%]  (Warmup) 
Chain 2 Iteration:  8300 / 20000 [ 41%]  (Warmup) 
Chain 2 Iteration:  8400 / 20000 [ 42%]  (Warmup) 
Chain 2 Iteration:  8500 / 20000 [ 42%]  (Warmup) 
Chain 2 Iteration:  8600 / 20000 [ 43%]  (Warmup) 
Chain 2 Iteration:  8700 / 20000 [ 43%]  (Warmup) 
Chain 2 Iteration:  8800 / 20000 [ 44%]  (Warmup) 
Chain 2 Iteration:  8900 / 20000 [ 44%]  (Warmup) 
Chain 2 Iteration:  9000 / 20000 [ 45%]  (Warmup) 
Chain 2 Iteration:  9100 / 20000 [ 45%]  (Warmup) 
Chain 2 Iteration:  9200 / 20000 [ 46%]  (Warmup) 
Chain 2 Iteration:  9300 / 20000 [ 46%]  (Warmup) 
Chain 2 Iteration:  9400 / 20000 [ 47%]  (Warmup) 
Chain 2 Iteration:  9500 / 20000 [ 47%]  (Warmup) 
Chain 2 Iteration:  9600 / 20000 [ 48%]  (Warmup) 
Chain 2 Iteration:  9700 / 20000 [ 48%]  (Warmup) 
Chain 2 Iteration:  9800 / 20000 [ 49%]  (Warmup) 
Chain 2 Iteration:  9900 / 20000 [ 49%]  (Warmup) 
Chain 2 Iteration: 10000 / 20000 [ 50%]  (Warmup) 
Chain 2 Iteration: 10001 / 20000 [ 50%]  (Sampling) 
Chain 2 Iteration: 10100 / 20000 [ 50%]  (Sampling) 
Chain 2 Iteration: 10200 / 20000 [ 51%]  (Sampling) 
Chain 2 Iteration: 10300 / 20000 [ 51%]  (Sampling) 
Chain 2 Iteration: 10400 / 20000 [ 52%]  (Sampling) 
Chain 2 Iteration: 10500 / 20000 [ 52%]  (Sampling) 
Chain 2 Iteration: 10600 / 20000 [ 53%]  (Sampling) 
Chain 2 Iteration: 10700 / 20000 [ 53%]  (Sampling) 
Chain 2 Iteration: 10800 / 20000 [ 54%]  (Sampling) 
Chain 2 Iteration: 10900 / 20000 [ 54%]  (Sampling) 
Chain 2 Iteration: 11000 / 20000 [ 55%]  (Sampling) 
Chain 2 Iteration: 11100 / 20000 [ 55%]  (Sampling) 
Chain 2 Iteration: 11200 / 20000 [ 56%]  (Sampling) 
Chain 2 Iteration: 11300 / 20000 [ 56%]  (Sampling) 
Chain 2 Iteration: 11400 / 20000 [ 57%]  (Sampling) 
Chain 2 Iteration: 11500 / 20000 [ 57%]  (Sampling) 
Chain 2 Iteration: 11600 / 20000 [ 58%]  (Sampling) 
Chain 2 Iteration: 11700 / 20000 [ 58%]  (Sampling) 
Chain 2 Iteration: 11800 / 20000 [ 59%]  (Sampling) 
Chain 2 Iteration: 11900 / 20000 [ 59%]  (Sampling) 
Chain 2 Iteration: 12000 / 20000 [ 60%]  (Sampling) 
Chain 2 Iteration: 12100 / 20000 [ 60%]  (Sampling) 
Chain 2 Iteration: 12200 / 20000 [ 61%]  (Sampling) 
Chain 2 Iteration: 12300 / 20000 [ 61%]  (Sampling) 
Chain 2 Iteration: 12400 / 20000 [ 62%]  (Sampling) 
Chain 2 Iteration: 12500 / 20000 [ 62%]  (Sampling) 
Chain 2 Iteration: 12600 / 20000 [ 63%]  (Sampling) 
Chain 2 Iteration: 12700 / 20000 [ 63%]  (Sampling) 
Chain 2 Iteration: 12800 / 20000 [ 64%]  (Sampling) 
Chain 2 Iteration: 12900 / 20000 [ 64%]  (Sampling) 
Chain 2 Iteration: 13000 / 20000 [ 65%]  (Sampling) 
Chain 2 Iteration: 13100 / 20000 [ 65%]  (Sampling) 
Chain 2 Iteration: 13200 / 20000 [ 66%]  (Sampling) 
Chain 2 Iteration: 13300 / 20000 [ 66%]  (Sampling) 
Chain 2 Iteration: 13400 / 20000 [ 67%]  (Sampling) 
Chain 2 Iteration: 13500 / 20000 [ 67%]  (Sampling) 
Chain 2 Iteration: 13600 / 20000 [ 68%]  (Sampling) 
Chain 2 Iteration: 13700 / 20000 [ 68%]  (Sampling) 
Chain 2 Iteration: 13800 / 20000 [ 69%]  (Sampling) 
Chain 2 Iteration: 13900 / 20000 [ 69%]  (Sampling) 
Chain 2 Iteration: 14000 / 20000 [ 70%]  (Sampling) 
Chain 2 Iteration: 14100 / 20000 [ 70%]  (Sampling) 
Chain 2 Iteration: 14200 / 20000 [ 71%]  (Sampling) 
Chain 2 Iteration: 14300 / 20000 [ 71%]  (Sampling) 
Chain 3 Iteration:     1 / 20000 [  0%]  (Warmup) 
Chain 3 Iteration:   100 / 20000 [  0%]  (Warmup) 
Chain 3 Iteration:   200 / 20000 [  1%]  (Warmup) 
Chain 3 Iteration:   300 / 20000 [  1%]  (Warmup) 
Chain 3 Iteration:   400 / 20000 [  2%]  (Warmup) 
Chain 3 Iteration:   500 / 20000 [  2%]  (Warmup) 
Chain 3 Iteration:   600 / 20000 [  3%]  (Warmup) 
Chain 3 Iteration:   700 / 20000 [  3%]  (Warmup) 
Chain 3 Iteration:   800 / 20000 [  4%]  (Warmup) 
Chain 3 Iteration:   900 / 20000 [  4%]  (Warmup) 
Chain 3 Iteration:  1000 / 20000 [  5%]  (Warmup) 
Chain 3 Iteration:  1100 / 20000 [  5%]  (Warmup) 
Chain 3 Iteration:  1200 / 20000 [  6%]  (Warmup) 
Chain 3 Iteration:  1300 / 20000 [  6%]  (Warmup) 
Chain 3 Iteration:  1400 / 20000 [  7%]  (Warmup) 
Chain 3 Iteration:  1500 / 20000 [  7%]  (Warmup) 
Chain 3 Iteration:  1600 / 20000 [  8%]  (Warmup) 
Chain 3 Iteration:  1700 / 20000 [  8%]  (Warmup) 
Chain 3 Iteration:  1800 / 20000 [  9%]  (Warmup) 
Chain 3 Iteration:  1900 / 20000 [  9%]  (Warmup) 
Chain 3 Iteration:  2000 / 20000 [ 10%]  (Warmup) 
Chain 3 Iteration:  2100 / 20000 [ 10%]  (Warmup) 
Chain 3 Iteration:  2200 / 20000 [ 11%]  (Warmup) 
Chain 3 Iteration:  2300 / 20000 [ 11%]  (Warmup) 
Chain 3 Iteration:  2400 / 20000 [ 12%]  (Warmup) 
Chain 3 Iteration:  2500 / 20000 [ 12%]  (Warmup) 
Chain 3 Iteration:  2600 / 20000 [ 13%]  (Warmup) 
Chain 3 Iteration:  2700 / 20000 [ 13%]  (Warmup) 
Chain 3 Iteration:  2800 / 20000 [ 14%]  (Warmup) 
Chain 3 Iteration:  2900 / 20000 [ 14%]  (Warmup) 
Chain 3 Iteration:  3000 / 20000 [ 15%]  (Warmup) 
Chain 3 Iteration:  3100 / 20000 [ 15%]  (Warmup) 
Chain 3 Iteration:  3200 / 20000 [ 16%]  (Warmup) 
Chain 3 Iteration:  3300 / 20000 [ 16%]  (Warmup) 
Chain 3 Iteration:  3400 / 20000 [ 17%]  (Warmup) 
Chain 3 Iteration:  3500 / 20000 [ 17%]  (Warmup) 
Chain 3 Iteration:  3600 / 20000 [ 18%]  (Warmup) 
Chain 3 Iteration:  3700 / 20000 [ 18%]  (Warmup) 
Chain 3 Iteration:  3800 / 20000 [ 19%]  (Warmup) 
Chain 3 Iteration:  3900 / 20000 [ 19%]  (Warmup) 
Chain 3 Iteration:  4000 / 20000 [ 20%]  (Warmup) 
Chain 3 Iteration:  4100 / 20000 [ 20%]  (Warmup) 
Chain 3 Iteration:  4200 / 20000 [ 21%]  (Warmup) 
Chain 3 Iteration:  4300 / 20000 [ 21%]  (Warmup) 
Chain 3 Iteration:  4400 / 20000 [ 22%]  (Warmup) 
Chain 3 Iteration:  4500 / 20000 [ 22%]  (Warmup) 
Chain 3 Iteration:  4600 / 20000 [ 23%]  (Warmup) 
Chain 3 Iteration:  4700 / 20000 [ 23%]  (Warmup) 
Chain 3 Iteration:  4800 / 20000 [ 24%]  (Warmup) 
Chain 3 Iteration:  4900 / 20000 [ 24%]  (Warmup) 
Chain 3 Iteration:  5000 / 20000 [ 25%]  (Warmup) 
Chain 3 Iteration:  5100 / 20000 [ 25%]  (Warmup) 
Chain 3 Iteration:  5200 / 20000 [ 26%]  (Warmup) 
Chain 3 Iteration:  5300 / 20000 [ 26%]  (Warmup) 
Chain 3 Iteration:  5400 / 20000 [ 27%]  (Warmup) 
Chain 3 Iteration:  5500 / 20000 [ 27%]  (Warmup) 
Chain 3 Iteration:  5600 / 20000 [ 28%]  (Warmup) 
Chain 3 Iteration:  5700 / 20000 [ 28%]  (Warmup) 
Chain 3 Iteration:  5800 / 20000 [ 29%]  (Warmup) 
Chain 3 Iteration:  5900 / 20000 [ 29%]  (Warmup) 
Chain 3 Iteration:  6000 / 20000 [ 30%]  (Warmup) 
Chain 3 Iteration:  6100 / 20000 [ 30%]  (Warmup) 
Chain 3 Iteration:  6200 / 20000 [ 31%]  (Warmup) 
Chain 3 Iteration:  6300 / 20000 [ 31%]  (Warmup) 
Chain 3 Iteration:  6400 / 20000 [ 32%]  (Warmup) 
Chain 3 Iteration:  6500 / 20000 [ 32%]  (Warmup) 
Chain 3 Iteration:  6600 / 20000 [ 33%]  (Warmup) 
Chain 3 Iteration:  6700 / 20000 [ 33%]  (Warmup) 
Chain 3 Iteration:  6800 / 20000 [ 34%]  (Warmup) 
Chain 3 Iteration:  6900 / 20000 [ 34%]  (Warmup) 
Chain 3 Iteration:  7000 / 20000 [ 35%]  (Warmup) 
Chain 3 Iteration:  7100 / 20000 [ 35%]  (Warmup) 
Chain 3 Iteration:  7200 / 20000 [ 36%]  (Warmup) 
Chain 3 Iteration:  7300 / 20000 [ 36%]  (Warmup) 
Chain 3 Iteration:  7400 / 20000 [ 37%]  (Warmup) 
Chain 3 Iteration:  7500 / 20000 [ 37%]  (Warmup) 
Chain 3 Iteration:  7600 / 20000 [ 38%]  (Warmup) 
Chain 3 Iteration:  7700 / 20000 [ 38%]  (Warmup) 
Chain 3 Iteration:  7800 / 20000 [ 39%]  (Warmup) 
Chain 3 Iteration:  7900 / 20000 [ 39%]  (Warmup) 
Chain 3 Iteration:  8000 / 20000 [ 40%]  (Warmup) 
Chain 3 Iteration:  8100 / 20000 [ 40%]  (Warmup) 
Chain 3 Iteration:  8200 / 20000 [ 41%]  (Warmup) 
Chain 3 Iteration:  8300 / 20000 [ 41%]  (Warmup) 
Chain 3 Iteration:  8400 / 20000 [ 42%]  (Warmup) 
Chain 3 Iteration:  8500 / 20000 [ 42%]  (Warmup) 
Chain 3 Iteration:  8600 / 20000 [ 43%]  (Warmup) 
Chain 3 Iteration:  8700 / 20000 [ 43%]  (Warmup) 
Chain 3 Iteration:  8800 / 20000 [ 44%]  (Warmup) 
Chain 3 Iteration:  8900 / 20000 [ 44%]  (Warmup) 
Chain 3 Iteration:  9000 / 20000 [ 45%]  (Warmup) 
Chain 3 Iteration:  9100 / 20000 [ 45%]  (Warmup) 
Chain 3 Iteration:  9200 / 20000 [ 46%]  (Warmup) 
Chain 3 Iteration:  9300 / 20000 [ 46%]  (Warmup) 
Chain 3 Iteration:  9400 / 20000 [ 47%]  (Warmup) 
Chain 3 Iteration:  9500 / 20000 [ 47%]  (Warmup) 
Chain 3 Iteration:  9600 / 20000 [ 48%]  (Warmup) 
Chain 3 Iteration:  9700 / 20000 [ 48%]  (Warmup) 
Chain 3 Iteration:  9800 / 20000 [ 49%]  (Warmup) 
Chain 3 Iteration:  9900 / 20000 [ 49%]  (Warmup) 
Chain 3 Iteration: 10000 / 20000 [ 50%]  (Warmup) 
Chain 3 Iteration: 10001 / 20000 [ 50%]  (Sampling) 
Chain 3 Iteration: 10100 / 20000 [ 50%]  (Sampling) 
Chain 3 Iteration: 10200 / 20000 [ 51%]  (Sampling) 
Chain 3 Iteration: 10300 / 20000 [ 51%]  (Sampling) 
Chain 3 Iteration: 10400 / 20000 [ 52%]  (Sampling) 
Chain 3 Iteration: 10500 / 20000 [ 52%]  (Sampling) 
Chain 3 Iteration: 10600 / 20000 [ 53%]  (Sampling) 
Chain 3 Iteration: 10700 / 20000 [ 53%]  (Sampling) 
Chain 3 Iteration: 10800 / 20000 [ 54%]  (Sampling) 
Chain 3 Iteration: 10900 / 20000 [ 54%]  (Sampling) 
Chain 3 Iteration: 11000 / 20000 [ 55%]  (Sampling) 
Chain 3 Iteration: 11100 / 20000 [ 55%]  (Sampling) 
Chain 3 Iteration: 11200 / 20000 [ 56%]  (Sampling) 
Chain 3 Iteration: 11300 / 20000 [ 56%]  (Sampling) 
Chain 3 Iteration: 11400 / 20000 [ 57%]  (Sampling) 
Chain 3 Iteration: 11500 / 20000 [ 57%]  (Sampling) 
Chain 3 Iteration: 11600 / 20000 [ 58%]  (Sampling) 
Chain 3 Iteration: 11700 / 20000 [ 58%]  (Sampling) 
Chain 3 Iteration: 11800 / 20000 [ 59%]  (Sampling) 
Chain 3 Iteration: 11900 / 20000 [ 59%]  (Sampling) 
Chain 3 Iteration: 12000 / 20000 [ 60%]  (Sampling) 
Chain 3 Iteration: 12100 / 20000 [ 60%]  (Sampling) 
Chain 3 Iteration: 12200 / 20000 [ 61%]  (Sampling) 
Chain 3 Iteration: 12300 / 20000 [ 61%]  (Sampling) 
Chain 3 Iteration: 12400 / 20000 [ 62%]  (Sampling) 
Chain 3 Iteration: 12500 / 20000 [ 62%]  (Sampling) 
Chain 3 Iteration: 12600 / 20000 [ 63%]  (Sampling) 
Chain 3 Iteration: 12700 / 20000 [ 63%]  (Sampling) 
Chain 3 Iteration: 12800 / 20000 [ 64%]  (Sampling) 
Chain 3 Iteration: 12900 / 20000 [ 64%]  (Sampling) 
Chain 3 Iteration: 13000 / 20000 [ 65%]  (Sampling) 
Chain 3 Iteration: 13100 / 20000 [ 65%]  (Sampling) 
Chain 3 Iteration: 13200 / 20000 [ 66%]  (Sampling) 
Chain 3 Iteration: 13300 / 20000 [ 66%]  (Sampling) 
Chain 3 Iteration: 13400 / 20000 [ 67%]  (Sampling) 
Chain 3 Iteration: 13500 / 20000 [ 67%]  (Sampling) 
Chain 3 Iteration: 13600 / 20000 [ 68%]  (Sampling) 
Chain 3 Iteration: 13700 / 20000 [ 68%]  (Sampling) 
Chain 3 Iteration: 13800 / 20000 [ 69%]  (Sampling) 
Chain 3 Iteration: 13900 / 20000 [ 69%]  (Sampling) 
Chain 3 Iteration: 14000 / 20000 [ 70%]  (Sampling) 
Chain 3 Iteration: 14100 / 20000 [ 70%]  (Sampling) 
Chain 3 Iteration: 14200 / 20000 [ 71%]  (Sampling) 
Chain 3 Iteration: 14300 / 20000 [ 71%]  (Sampling) 
Chain 3 Iteration: 14400 / 20000 [ 72%]  (Sampling) 
Chain 3 Iteration: 14500 / 20000 [ 72%]  (Sampling) 
Chain 3 Iteration: 14600 / 20000 [ 73%]  (Sampling) 
Chain 3 Iteration: 14700 / 20000 [ 73%]  (Sampling) 
Chain 4 Iteration:     1 / 20000 [  0%]  (Warmup) 
Chain 4 Iteration:   100 / 20000 [  0%]  (Warmup) 
Chain 4 Iteration:   200 / 20000 [  1%]  (Warmup) 
Chain 4 Iteration:   300 / 20000 [  1%]  (Warmup) 
Chain 4 Iteration:   400 / 20000 [  2%]  (Warmup) 
Chain 4 Iteration:   500 / 20000 [  2%]  (Warmup) 
Chain 4 Iteration:   600 / 20000 [  3%]  (Warmup) 
Chain 4 Iteration:   700 / 20000 [  3%]  (Warmup) 
Chain 4 Iteration:   800 / 20000 [  4%]  (Warmup) 
Chain 4 Iteration:   900 / 20000 [  4%]  (Warmup) 
Chain 4 Iteration:  1000 / 20000 [  5%]  (Warmup) 
Chain 4 Iteration:  1100 / 20000 [  5%]  (Warmup) 
Chain 4 Iteration:  1200 / 20000 [  6%]  (Warmup) 
Chain 4 Iteration:  1300 / 20000 [  6%]  (Warmup) 
Chain 4 Iteration:  1400 / 20000 [  7%]  (Warmup) 
Chain 4 Iteration:  1500 / 20000 [  7%]  (Warmup) 
Chain 4 Iteration:  1600 / 20000 [  8%]  (Warmup) 
Chain 4 Iteration:  1700 / 20000 [  8%]  (Warmup) 
Chain 4 Iteration:  1800 / 20000 [  9%]  (Warmup) 
Chain 4 Iteration:  1900 / 20000 [  9%]  (Warmup) 
Chain 4 Iteration:  2000 / 20000 [ 10%]  (Warmup) 
Chain 4 Iteration:  2100 / 20000 [ 10%]  (Warmup) 
Chain 4 Iteration:  2200 / 20000 [ 11%]  (Warmup) 
Chain 4 Iteration:  2300 / 20000 [ 11%]  (Warmup) 
Chain 4 Iteration:  2400 / 20000 [ 12%]  (Warmup) 
Chain 4 Iteration:  2500 / 20000 [ 12%]  (Warmup) 
Chain 4 Iteration:  2600 / 20000 [ 13%]  (Warmup) 
Chain 4 Iteration:  2700 / 20000 [ 13%]  (Warmup) 
Chain 4 Iteration:  2800 / 20000 [ 14%]  (Warmup) 
Chain 4 Iteration:  2900 / 20000 [ 14%]  (Warmup) 
Chain 4 Iteration:  3000 / 20000 [ 15%]  (Warmup) 
Chain 4 Iteration:  3100 / 20000 [ 15%]  (Warmup) 
Chain 4 Iteration:  3200 / 20000 [ 16%]  (Warmup) 
Chain 4 Iteration:  3300 / 20000 [ 16%]  (Warmup) 
Chain 4 Iteration:  3400 / 20000 [ 17%]  (Warmup) 
Chain 4 Iteration:  3500 / 20000 [ 17%]  (Warmup) 
Chain 4 Iteration:  3600 / 20000 [ 18%]  (Warmup) 
Chain 4 Iteration:  3700 / 20000 [ 18%]  (Warmup) 
Chain 4 Iteration:  3800 / 20000 [ 19%]  (Warmup) 
Chain 4 Iteration:  3900 / 20000 [ 19%]  (Warmup) 
Chain 4 Iteration:  4000 / 20000 [ 20%]  (Warmup) 
Chain 4 Iteration:  4100 / 20000 [ 20%]  (Warmup) 
Chain 4 Iteration:  4200 / 20000 [ 21%]  (Warmup) 
Chain 4 Iteration:  4300 / 20000 [ 21%]  (Warmup) 
Chain 4 Iteration:  4400 / 20000 [ 22%]  (Warmup) 
Chain 4 Iteration:  4500 / 20000 [ 22%]  (Warmup) 
Chain 4 Iteration:  4600 / 20000 [ 23%]  (Warmup) 
Chain 4 Iteration:  4700 / 20000 [ 23%]  (Warmup) 
Chain 4 Iteration:  4800 / 20000 [ 24%]  (Warmup) 
Chain 4 Iteration:  4900 / 20000 [ 24%]  (Warmup) 
Chain 4 Iteration:  5000 / 20000 [ 25%]  (Warmup) 
Chain 4 Iteration:  5100 / 20000 [ 25%]  (Warmup) 
Chain 4 Iteration:  5200 / 20000 [ 26%]  (Warmup) 
Chain 4 Iteration:  5300 / 20000 [ 26%]  (Warmup) 
Chain 4 Iteration:  5400 / 20000 [ 27%]  (Warmup) 
Chain 4 Iteration:  5500 / 20000 [ 27%]  (Warmup) 
Chain 4 Iteration:  5600 / 20000 [ 28%]  (Warmup) 
Chain 4 Iteration:  5700 / 20000 [ 28%]  (Warmup) 
Chain 4 Iteration:  5800 / 20000 [ 29%]  (Warmup) 
Chain 4 Iteration:  5900 / 20000 [ 29%]  (Warmup) 
Chain 4 Iteration:  6000 / 20000 [ 30%]  (Warmup) 
Chain 4 Iteration:  6100 / 20000 [ 30%]  (Warmup) 
Chain 4 Iteration:  6200 / 20000 [ 31%]  (Warmup) 
Chain 4 Iteration:  6300 / 20000 [ 31%]  (Warmup) 
Chain 4 Iteration:  6400 / 20000 [ 32%]  (Warmup) 
Chain 4 Iteration:  6500 / 20000 [ 32%]  (Warmup) 
Chain 4 Iteration:  6600 / 20000 [ 33%]  (Warmup) 
Chain 4 Iteration:  6700 / 20000 [ 33%]  (Warmup) 
Chain 4 Iteration:  6800 / 20000 [ 34%]  (Warmup) 
Chain 4 Iteration:  6900 / 20000 [ 34%]  (Warmup) 
Chain 4 Iteration:  7000 / 20000 [ 35%]  (Warmup) 
Chain 4 Iteration:  7100 / 20000 [ 35%]  (Warmup) 
Chain 4 Iteration:  7200 / 20000 [ 36%]  (Warmup) 
Chain 4 Iteration:  7300 / 20000 [ 36%]  (Warmup) 
Chain 4 Iteration:  7400 / 20000 [ 37%]  (Warmup) 
Chain 4 Iteration:  7500 / 20000 [ 37%]  (Warmup) 
Chain 4 Iteration:  7600 / 20000 [ 38%]  (Warmup) 
Chain 4 Iteration:  7700 / 20000 [ 38%]  (Warmup) 
Chain 4 Iteration:  7800 / 20000 [ 39%]  (Warmup) 
Chain 4 Iteration:  7900 / 20000 [ 39%]  (Warmup) 
Chain 4 Iteration:  8000 / 20000 [ 40%]  (Warmup) 
Chain 4 Iteration:  8100 / 20000 [ 40%]  (Warmup) 
Chain 4 Iteration:  8200 / 20000 [ 41%]  (Warmup) 
Chain 4 Iteration:  8300 / 20000 [ 41%]  (Warmup) 
Chain 4 Iteration:  8400 / 20000 [ 42%]  (Warmup) 
Chain 4 Iteration:  8500 / 20000 [ 42%]  (Warmup) 
Chain 4 Iteration:  8600 / 20000 [ 43%]  (Warmup) 
Chain 4 Iteration:  8700 / 20000 [ 43%]  (Warmup) 
Chain 4 Iteration:  8800 / 20000 [ 44%]  (Warmup) 
Chain 4 Iteration:  8900 / 20000 [ 44%]  (Warmup) 
Chain 4 Iteration:  9000 / 20000 [ 45%]  (Warmup) 
Chain 4 Iteration:  9100 / 20000 [ 45%]  (Warmup) 
Chain 4 Iteration:  9200 / 20000 [ 46%]  (Warmup) 
Chain 4 Iteration:  9300 / 20000 [ 46%]  (Warmup) 
Chain 4 Iteration:  9400 / 20000 [ 47%]  (Warmup) 
Chain 4 Iteration:  9500 / 20000 [ 47%]  (Warmup) 
Chain 4 Iteration:  9600 / 20000 [ 48%]  (Warmup) 
Chain 4 Iteration:  9700 / 20000 [ 48%]  (Warmup) 
Chain 4 Iteration:  9800 / 20000 [ 49%]  (Warmup) 
Chain 4 Iteration:  9900 / 20000 [ 49%]  (Warmup) 
Chain 4 Iteration: 10000 / 20000 [ 50%]  (Warmup) 
Chain 4 Iteration: 10001 / 20000 [ 50%]  (Sampling) 
Chain 4 Iteration: 10100 / 20000 [ 50%]  (Sampling) 
Chain 4 Iteration: 10200 / 20000 [ 51%]  (Sampling) 
Chain 4 Iteration: 10300 / 20000 [ 51%]  (Sampling) 
Chain 4 Iteration: 10400 / 20000 [ 52%]  (Sampling) 
Chain 4 Iteration: 10500 / 20000 [ 52%]  (Sampling) 
Chain 4 Iteration: 10600 / 20000 [ 53%]  (Sampling) 
Chain 4 Iteration: 10700 / 20000 [ 53%]  (Sampling) 
Chain 4 Iteration: 10800 / 20000 [ 54%]  (Sampling) 
Chain 4 Iteration: 10900 / 20000 [ 54%]  (Sampling) 
Chain 4 Iteration: 11000 / 20000 [ 55%]  (Sampling) 
Chain 4 Iteration: 11100 / 20000 [ 55%]  (Sampling) 
Chain 4 Iteration: 11200 / 20000 [ 56%]  (Sampling) 
Chain 4 Iteration: 11300 / 20000 [ 56%]  (Sampling) 
Chain 4 Iteration: 11400 / 20000 [ 57%]  (Sampling) 
Chain 4 Iteration: 11500 / 20000 [ 57%]  (Sampling) 
Chain 4 Iteration: 11600 / 20000 [ 58%]  (Sampling) 
Chain 4 Iteration: 11700 / 20000 [ 58%]  (Sampling) 
Chain 4 Iteration: 11800 / 20000 [ 59%]  (Sampling) 
Chain 4 Iteration: 11900 / 20000 [ 59%]  (Sampling) 
Chain 4 Iteration: 12000 / 20000 [ 60%]  (Sampling) 
Chain 4 Iteration: 12100 / 20000 [ 60%]  (Sampling) 
Chain 4 Iteration: 12200 / 20000 [ 61%]  (Sampling) 
Chain 4 Iteration: 12300 / 20000 [ 61%]  (Sampling) 
Chain 4 Iteration: 12400 / 20000 [ 62%]  (Sampling) 
Chain 4 Iteration: 12500 / 20000 [ 62%]  (Sampling) 
Chain 4 Iteration: 12600 / 20000 [ 63%]  (Sampling) 
Chain 4 Iteration: 12700 / 20000 [ 63%]  (Sampling) 
Chain 4 Iteration: 12800 / 20000 [ 64%]  (Sampling) 
Chain 4 Iteration: 12900 / 20000 [ 64%]  (Sampling) 
Chain 4 Iteration: 13000 / 20000 [ 65%]  (Sampling) 
Chain 4 Iteration: 13100 / 20000 [ 65%]  (Sampling) 
Chain 4 Iteration: 13200 / 20000 [ 66%]  (Sampling) 
Chain 4 Iteration: 13300 / 20000 [ 66%]  (Sampling) 
Chain 4 Iteration: 13400 / 20000 [ 67%]  (Sampling) 
Chain 4 Iteration: 13500 / 20000 [ 67%]  (Sampling) 
Chain 4 Iteration: 13600 / 20000 [ 68%]  (Sampling) 
Chain 4 Iteration: 13700 / 20000 [ 68%]  (Sampling) 
Chain 4 Iteration: 13800 / 20000 [ 69%]  (Sampling) 
Chain 4 Iteration: 13900 / 20000 [ 69%]  (Sampling) 
Chain 4 Iteration: 14000 / 20000 [ 70%]  (Sampling) 
Chain 4 Iteration: 14100 / 20000 [ 70%]  (Sampling) 
Chain 4 Iteration: 14200 / 20000 [ 71%]  (Sampling) 
Chain 4 Iteration: 14300 / 20000 [ 71%]  (Sampling) 
Chain 4 Iteration: 14400 / 20000 [ 72%]  (Sampling) 
Chain 4 Iteration: 14500 / 20000 [ 72%]  (Sampling) 
Chain 4 Iteration: 14600 / 20000 [ 73%]  (Sampling) 
Chain 4 Iteration: 14700 / 20000 [ 73%]  (Sampling) 
Chain 1 Iteration: 13700 / 20000 [ 68%]  (Sampling) 
Chain 1 Iteration: 13800 / 20000 [ 69%]  (Sampling) 
Chain 1 Iteration: 13900 / 20000 [ 69%]  (Sampling) 
Chain 1 Iteration: 14000 / 20000 [ 70%]  (Sampling) 
Chain 1 Iteration: 14100 / 20000 [ 70%]  (Sampling) 
Chain 1 Iteration: 14200 / 20000 [ 71%]  (Sampling) 
Chain 1 Iteration: 14300 / 20000 [ 71%]  (Sampling) 
Chain 1 Iteration: 14400 / 20000 [ 72%]  (Sampling) 
Chain 1 Iteration: 14500 / 20000 [ 72%]  (Sampling) 
Chain 1 Iteration: 14600 / 20000 [ 73%]  (Sampling) 
Chain 1 Iteration: 14700 / 20000 [ 73%]  (Sampling) 
Chain 1 Iteration: 14800 / 20000 [ 74%]  (Sampling) 
Chain 1 Iteration: 14900 / 20000 [ 74%]  (Sampling) 
Chain 1 Iteration: 15000 / 20000 [ 75%]  (Sampling) 
Chain 1 Iteration: 15100 / 20000 [ 75%]  (Sampling) 
Chain 1 Iteration: 15200 / 20000 [ 76%]  (Sampling) 
Chain 1 Iteration: 15300 / 20000 [ 76%]  (Sampling) 
Chain 1 Iteration: 15400 / 20000 [ 77%]  (Sampling) 
Chain 1 Iteration: 15500 / 20000 [ 77%]  (Sampling) 
Chain 1 Iteration: 15600 / 20000 [ 78%]  (Sampling) 
Chain 1 Iteration: 15700 / 20000 [ 78%]  (Sampling) 
Chain 1 Iteration: 15800 / 20000 [ 79%]  (Sampling) 
Chain 1 Iteration: 15900 / 20000 [ 79%]  (Sampling) 
Chain 1 Iteration: 16000 / 20000 [ 80%]  (Sampling) 
Chain 1 Iteration: 16100 / 20000 [ 80%]  (Sampling) 
Chain 1 Iteration: 16200 / 20000 [ 81%]  (Sampling) 
Chain 1 Iteration: 16300 / 20000 [ 81%]  (Sampling) 
Chain 1 Iteration: 16400 / 20000 [ 82%]  (Sampling) 
Chain 1 Iteration: 16500 / 20000 [ 82%]  (Sampling) 
Chain 1 Iteration: 16600 / 20000 [ 83%]  (Sampling) 
Chain 1 Iteration: 16700 / 20000 [ 83%]  (Sampling) 
Chain 1 Iteration: 16800 / 20000 [ 84%]  (Sampling) 
Chain 1 Iteration: 16900 / 20000 [ 84%]  (Sampling) 
Chain 1 Iteration: 17000 / 20000 [ 85%]  (Sampling) 
Chain 1 Iteration: 17100 / 20000 [ 85%]  (Sampling) 
Chain 1 Iteration: 17200 / 20000 [ 86%]  (Sampling) 
Chain 1 Iteration: 17300 / 20000 [ 86%]  (Sampling) 
Chain 1 Iteration: 17400 / 20000 [ 87%]  (Sampling) 
Chain 1 Iteration: 17500 / 20000 [ 87%]  (Sampling) 
Chain 1 Iteration: 17600 / 20000 [ 88%]  (Sampling) 
Chain 1 Iteration: 17700 / 20000 [ 88%]  (Sampling) 
Chain 1 Iteration: 17800 / 20000 [ 89%]  (Sampling) 
Chain 1 Iteration: 17900 / 20000 [ 89%]  (Sampling) 
Chain 1 Iteration: 18000 / 20000 [ 90%]  (Sampling) 
Chain 1 Iteration: 18100 / 20000 [ 90%]  (Sampling) 
Chain 1 Iteration: 18200 / 20000 [ 91%]  (Sampling) 
Chain 1 Iteration: 18300 / 20000 [ 91%]  (Sampling) 
Chain 1 Iteration: 18400 / 20000 [ 92%]  (Sampling) 
Chain 1 Iteration: 18500 / 20000 [ 92%]  (Sampling) 
Chain 1 Iteration: 18600 / 20000 [ 93%]  (Sampling) 
Chain 1 Iteration: 18700 / 20000 [ 93%]  (Sampling) 
Chain 1 Iteration: 18800 / 20000 [ 94%]  (Sampling) 
Chain 1 Iteration: 18900 / 20000 [ 94%]  (Sampling) 
Chain 1 Iteration: 19000 / 20000 [ 95%]  (Sampling) 
Chain 1 Iteration: 19100 / 20000 [ 95%]  (Sampling) 
Chain 1 Iteration: 19200 / 20000 [ 96%]  (Sampling) 
Chain 1 Iteration: 19300 / 20000 [ 96%]  (Sampling) 
Chain 1 Iteration: 19400 / 20000 [ 97%]  (Sampling) 
Chain 1 Iteration: 19500 / 20000 [ 97%]  (Sampling) 
Chain 1 Iteration: 19600 / 20000 [ 98%]  (Sampling) 
Chain 1 Iteration: 19700 / 20000 [ 98%]  (Sampling) 
Chain 1 Iteration: 19800 / 20000 [ 99%]  (Sampling) 
Chain 1 Iteration: 19900 / 20000 [ 99%]  (Sampling) 
Chain 1 Iteration: 20000 / 20000 [100%]  (Sampling) 
Chain 2 Iteration: 14400 / 20000 [ 72%]  (Sampling) 
Chain 2 Iteration: 14500 / 20000 [ 72%]  (Sampling) 
Chain 2 Iteration: 14600 / 20000 [ 73%]  (Sampling) 
Chain 2 Iteration: 14700 / 20000 [ 73%]  (Sampling) 
Chain 2 Iteration: 14800 / 20000 [ 74%]  (Sampling) 
Chain 2 Iteration: 14900 / 20000 [ 74%]  (Sampling) 
Chain 2 Iteration: 15000 / 20000 [ 75%]  (Sampling) 
Chain 2 Iteration: 15100 / 20000 [ 75%]  (Sampling) 
Chain 2 Iteration: 15200 / 20000 [ 76%]  (Sampling) 
Chain 2 Iteration: 15300 / 20000 [ 76%]  (Sampling) 
Chain 2 Iteration: 15400 / 20000 [ 77%]  (Sampling) 
Chain 2 Iteration: 15500 / 20000 [ 77%]  (Sampling) 
Chain 2 Iteration: 15600 / 20000 [ 78%]  (Sampling) 
Chain 2 Iteration: 15700 / 20000 [ 78%]  (Sampling) 
Chain 2 Iteration: 15800 / 20000 [ 79%]  (Sampling) 
Chain 2 Iteration: 15900 / 20000 [ 79%]  (Sampling) 
Chain 2 Iteration: 16000 / 20000 [ 80%]  (Sampling) 
Chain 2 Iteration: 16100 / 20000 [ 80%]  (Sampling) 
Chain 2 Iteration: 16200 / 20000 [ 81%]  (Sampling) 
Chain 2 Iteration: 16300 / 20000 [ 81%]  (Sampling) 
Chain 2 Iteration: 16400 / 20000 [ 82%]  (Sampling) 
Chain 2 Iteration: 16500 / 20000 [ 82%]  (Sampling) 
Chain 2 Iteration: 16600 / 20000 [ 83%]  (Sampling) 
Chain 2 Iteration: 16700 / 20000 [ 83%]  (Sampling) 
Chain 2 Iteration: 16800 / 20000 [ 84%]  (Sampling) 
Chain 2 Iteration: 16900 / 20000 [ 84%]  (Sampling) 
Chain 2 Iteration: 17000 / 20000 [ 85%]  (Sampling) 
Chain 2 Iteration: 17100 / 20000 [ 85%]  (Sampling) 
Chain 2 Iteration: 17200 / 20000 [ 86%]  (Sampling) 
Chain 2 Iteration: 17300 / 20000 [ 86%]  (Sampling) 
Chain 2 Iteration: 17400 / 20000 [ 87%]  (Sampling) 
Chain 2 Iteration: 17500 / 20000 [ 87%]  (Sampling) 
Chain 2 Iteration: 17600 / 20000 [ 88%]  (Sampling) 
Chain 2 Iteration: 17700 / 20000 [ 88%]  (Sampling) 
Chain 2 Iteration: 17800 / 20000 [ 89%]  (Sampling) 
Chain 2 Iteration: 17900 / 20000 [ 89%]  (Sampling) 
Chain 2 Iteration: 18000 / 20000 [ 90%]  (Sampling) 
Chain 2 Iteration: 18100 / 20000 [ 90%]  (Sampling) 
Chain 2 Iteration: 18200 / 20000 [ 91%]  (Sampling) 
Chain 2 Iteration: 18300 / 20000 [ 91%]  (Sampling) 
Chain 2 Iteration: 18400 / 20000 [ 92%]  (Sampling) 
Chain 2 Iteration: 18500 / 20000 [ 92%]  (Sampling) 
Chain 2 Iteration: 18600 / 20000 [ 93%]  (Sampling) 
Chain 2 Iteration: 18700 / 20000 [ 93%]  (Sampling) 
Chain 2 Iteration: 18800 / 20000 [ 94%]  (Sampling) 
Chain 2 Iteration: 18900 / 20000 [ 94%]  (Sampling) 
Chain 2 Iteration: 19000 / 20000 [ 95%]  (Sampling) 
Chain 2 Iteration: 19100 / 20000 [ 95%]  (Sampling) 
Chain 2 Iteration: 19200 / 20000 [ 96%]  (Sampling) 
Chain 2 Iteration: 19300 / 20000 [ 96%]  (Sampling) 
Chain 2 Iteration: 19400 / 20000 [ 97%]  (Sampling) 
Chain 2 Iteration: 19500 / 20000 [ 97%]  (Sampling) 
Chain 2 Iteration: 19600 / 20000 [ 98%]  (Sampling) 
Chain 2 Iteration: 19700 / 20000 [ 98%]  (Sampling) 
Chain 2 Iteration: 19800 / 20000 [ 99%]  (Sampling) 
Chain 2 Iteration: 19900 / 20000 [ 99%]  (Sampling) 
Chain 2 Iteration: 20000 / 20000 [100%]  (Sampling) 
Chain 3 Iteration: 14800 / 20000 [ 74%]  (Sampling) 
Chain 3 Iteration: 14900 / 20000 [ 74%]  (Sampling) 
Chain 3 Iteration: 15000 / 20000 [ 75%]  (Sampling) 
Chain 3 Iteration: 15100 / 20000 [ 75%]  (Sampling) 
Chain 3 Iteration: 15200 / 20000 [ 76%]  (Sampling) 
Chain 3 Iteration: 15300 / 20000 [ 76%]  (Sampling) 
Chain 3 Iteration: 15400 / 20000 [ 77%]  (Sampling) 
Chain 3 Iteration: 15500 / 20000 [ 77%]  (Sampling) 
Chain 3 Iteration: 15600 / 20000 [ 78%]  (Sampling) 
Chain 3 Iteration: 15700 / 20000 [ 78%]  (Sampling) 
Chain 3 Iteration: 15800 / 20000 [ 79%]  (Sampling) 
Chain 3 Iteration: 15900 / 20000 [ 79%]  (Sampling) 
Chain 3 Iteration: 16000 / 20000 [ 80%]  (Sampling) 
Chain 3 Iteration: 16100 / 20000 [ 80%]  (Sampling) 
Chain 3 Iteration: 16200 / 20000 [ 81%]  (Sampling) 
Chain 3 Iteration: 16300 / 20000 [ 81%]  (Sampling) 
Chain 3 Iteration: 16400 / 20000 [ 82%]  (Sampling) 
Chain 3 Iteration: 16500 / 20000 [ 82%]  (Sampling) 
Chain 3 Iteration: 16600 / 20000 [ 83%]  (Sampling) 
Chain 3 Iteration: 16700 / 20000 [ 83%]  (Sampling) 
Chain 3 Iteration: 16800 / 20000 [ 84%]  (Sampling) 
Chain 3 Iteration: 16900 / 20000 [ 84%]  (Sampling) 
Chain 3 Iteration: 17000 / 20000 [ 85%]  (Sampling) 
Chain 3 Iteration: 17100 / 20000 [ 85%]  (Sampling) 
Chain 3 Iteration: 17200 / 20000 [ 86%]  (Sampling) 
Chain 3 Iteration: 17300 / 20000 [ 86%]  (Sampling) 
Chain 3 Iteration: 17400 / 20000 [ 87%]  (Sampling) 
Chain 3 Iteration: 17500 / 20000 [ 87%]  (Sampling) 
Chain 3 Iteration: 17600 / 20000 [ 88%]  (Sampling) 
Chain 3 Iteration: 17700 / 20000 [ 88%]  (Sampling) 
Chain 3 Iteration: 17800 / 20000 [ 89%]  (Sampling) 
Chain 3 Iteration: 17900 / 20000 [ 89%]  (Sampling) 
Chain 3 Iteration: 18000 / 20000 [ 90%]  (Sampling) 
Chain 3 Iteration: 18100 / 20000 [ 90%]  (Sampling) 
Chain 3 Iteration: 18200 / 20000 [ 91%]  (Sampling) 
Chain 3 Iteration: 18300 / 20000 [ 91%]  (Sampling) 
Chain 3 Iteration: 18400 / 20000 [ 92%]  (Sampling) 
Chain 3 Iteration: 18500 / 20000 [ 92%]  (Sampling) 
Chain 3 Iteration: 18600 / 20000 [ 93%]  (Sampling) 
Chain 3 Iteration: 18700 / 20000 [ 93%]  (Sampling) 
Chain 3 Iteration: 18800 / 20000 [ 94%]  (Sampling) 
Chain 3 Iteration: 18900 / 20000 [ 94%]  (Sampling) 
Chain 3 Iteration: 19000 / 20000 [ 95%]  (Sampling) 
Chain 3 Iteration: 19100 / 20000 [ 95%]  (Sampling) 
Chain 3 Iteration: 19200 / 20000 [ 96%]  (Sampling) 
Chain 3 Iteration: 19300 / 20000 [ 96%]  (Sampling) 
Chain 3 Iteration: 19400 / 20000 [ 97%]  (Sampling) 
Chain 3 Iteration: 19500 / 20000 [ 97%]  (Sampling) 
Chain 3 Iteration: 19600 / 20000 [ 98%]  (Sampling) 
Chain 3 Iteration: 19700 / 20000 [ 98%]  (Sampling) 
Chain 3 Iteration: 19800 / 20000 [ 99%]  (Sampling) 
Chain 3 Iteration: 19900 / 20000 [ 99%]  (Sampling) 
Chain 3 Iteration: 20000 / 20000 [100%]  (Sampling) 
Chain 4 Iteration: 14800 / 20000 [ 74%]  (Sampling) 
Chain 4 Iteration: 14900 / 20000 [ 74%]  (Sampling) 
Chain 4 Iteration: 15000 / 20000 [ 75%]  (Sampling) 
Chain 4 Iteration: 15100 / 20000 [ 75%]  (Sampling) 
Chain 4 Iteration: 15200 / 20000 [ 76%]  (Sampling) 
Chain 4 Iteration: 15300 / 20000 [ 76%]  (Sampling) 
Chain 4 Iteration: 15400 / 20000 [ 77%]  (Sampling) 
Chain 4 Iteration: 15500 / 20000 [ 77%]  (Sampling) 
Chain 4 Iteration: 15600 / 20000 [ 78%]  (Sampling) 
Chain 4 Iteration: 15700 / 20000 [ 78%]  (Sampling) 
Chain 4 Iteration: 15800 / 20000 [ 79%]  (Sampling) 
Chain 4 Iteration: 15900 / 20000 [ 79%]  (Sampling) 
Chain 4 Iteration: 16000 / 20000 [ 80%]  (Sampling) 
Chain 4 Iteration: 16100 / 20000 [ 80%]  (Sampling) 
Chain 4 Iteration: 16200 / 20000 [ 81%]  (Sampling) 
Chain 4 Iteration: 16300 / 20000 [ 81%]  (Sampling) 
Chain 4 Iteration: 16400 / 20000 [ 82%]  (Sampling) 
Chain 4 Iteration: 16500 / 20000 [ 82%]  (Sampling) 
Chain 4 Iteration: 16600 / 20000 [ 83%]  (Sampling) 
Chain 4 Iteration: 16700 / 20000 [ 83%]  (Sampling) 
Chain 4 Iteration: 16800 / 20000 [ 84%]  (Sampling) 
Chain 4 Iteration: 16900 / 20000 [ 84%]  (Sampling) 
Chain 4 Iteration: 17000 / 20000 [ 85%]  (Sampling) 
Chain 4 Iteration: 17100 / 20000 [ 85%]  (Sampling) 
Chain 4 Iteration: 17200 / 20000 [ 86%]  (Sampling) 
Chain 4 Iteration: 17300 / 20000 [ 86%]  (Sampling) 
Chain 4 Iteration: 17400 / 20000 [ 87%]  (Sampling) 
Chain 4 Iteration: 17500 / 20000 [ 87%]  (Sampling) 
Chain 4 Iteration: 17600 / 20000 [ 88%]  (Sampling) 
Chain 4 Iteration: 17700 / 20000 [ 88%]  (Sampling) 
Chain 4 Iteration: 17800 / 20000 [ 89%]  (Sampling) 
Chain 4 Iteration: 17900 / 20000 [ 89%]  (Sampling) 
Chain 4 Iteration: 18000 / 20000 [ 90%]  (Sampling) 
Chain 4 Iteration: 18100 / 20000 [ 90%]  (Sampling) 
Chain 4 Iteration: 18200 / 20000 [ 91%]  (Sampling) 
Chain 4 Iteration: 18300 / 20000 [ 91%]  (Sampling) 
Chain 4 Iteration: 18400 / 20000 [ 92%]  (Sampling) 
Chain 4 Iteration: 18500 / 20000 [ 92%]  (Sampling) 
Chain 4 Iteration: 18600 / 20000 [ 93%]  (Sampling) 
Chain 4 Iteration: 18700 / 20000 [ 93%]  (Sampling) 
Chain 4 Iteration: 18800 / 20000 [ 94%]  (Sampling) 
Chain 4 Iteration: 18900 / 20000 [ 94%]  (Sampling) 
Chain 4 Iteration: 19000 / 20000 [ 95%]  (Sampling) 
Chain 4 Iteration: 19100 / 20000 [ 95%]  (Sampling) 
Chain 4 Iteration: 19200 / 20000 [ 96%]  (Sampling) 
Chain 4 Iteration: 19300 / 20000 [ 96%]  (Sampling) 
Chain 4 Iteration: 19400 / 20000 [ 97%]  (Sampling) 
Chain 4 Iteration: 19500 / 20000 [ 97%]  (Sampling) 
Chain 4 Iteration: 19600 / 20000 [ 98%]  (Sampling) 
Chain 4 Iteration: 19700 / 20000 [ 98%]  (Sampling) 
Chain 4 Iteration: 19800 / 20000 [ 99%]  (Sampling) 
Chain 4 Iteration: 19900 / 20000 [ 99%]  (Sampling) 
Chain 4 Iteration: 20000 / 20000 [100%]  (Sampling) 
Chain 1 finished in 0.3 seconds.
Chain 2 finished in 0.3 seconds.
Chain 3 finished in 0.3 seconds.
Chain 4 finished in 0.3 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.3 seconds.
Total execution time: 0.4 seconds.

• Within the compiled program and the data, the next step is to run the Markov Chain Monte Carlo (MCMC) sampling (this is basically equivalent to drawing from a posterior distribution)

• In cmdstanr, running the MCMC sampling comes from the $sample() function that is part of the compiled program object

Running Markov Chains in rstan

rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

# example MCMC analysis in rstan
model00.rstan = stan(
  model_code = stanModel,
  model_name = "Empty model",
  data = stanData,
  warmup = 10000,
  iter = 20000,
  chains = 4,
  verbose = TRUE
)

1

The first two lines of syntax enable running one chain per thread (parallel processing)

2

Use stan() to compile and sample posterior distribution

3

iter represents number of sampling and warmup iterations

MCMC Process

• The MCMC algorithm runs as a series of discrete iterations

• Within each iteration, each parameters in the model has an opportunity to change its value

  • For each parameter, a new parameter is sampled at random from the current belief of posterior distribution

• In Stan (Hamiltonian Monte Carlo), for a given iteration, a proposed parameter is generated

  • The posterior likelihood “values” (more than just density; includes likelihood of proposal) are calculated for the current and proposed values of the parameter

  • Make a decision: the proposed values are accepted based on the draw of a uniform number compared to transition probability (random walk)

• If all models are specified correctly, then regardless of starting location, each chain will converge to the posterior if running long enough

  • But, the chains must be checked for convergence when the algorithm stops (diagnosis)

Example of Poor Convergence

EmptyModelPoor.stan

model {
  beta0 ~ normal(50, 10); // prior for beta0
  sigma ~ uniform(0, 10); // prior for sigma
  y ~ normal(beta0, sigma); // model for observed data
}

DietDataExample.R

## Model 0 with poor convergence
model00Poor.fromFile = cmdstan_model(stan_file = "Code/EmptyModelPoor.stan")
model00Poor.samples = model00Poor.fromFile$sample(
  data = stanData,
  seed = 1,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 10000,
  iter_sampling = 10000,
  refresh = 0
)

DietDataExample.R

model00Poor.samples$summary()[c('variable','mean', 'rhat')]

# A tibble: 3 × 3
  variable      mean  rhat
  <chr>        <dbl> <dbl>
1 lp__     -4853.     3.54
2 beta0       -0.593  4.13
3 sigma       10.0    1.00

bayesplot::mcmc_trace(model00Poor.samples$draws("beta0"))

Markov Chain Convergence Diagnosis

1. Once Stan stops, the next step is to determine if the chains converged to their posterior distribution
   • This is called convergence diagnosis
2. Many methods have been developed for diagnosing if Markov chains have converged
   • Two most common: visual inspection and Gelman-Rubin Potential Scale Reduction Factor (PSRF)
   • Visual inspection
     • Expect no trends in timeseries - should look like a catapillar
     • Shape of posterior density should be mostly smooth
   • Gelman-Rubin PSRF (denoted as \(\hat{R}\))
     • For analyses with multiple chains
     • Ratio of between-chain variance to within-chain variance
     • Should be near 1 (maximum somewhere under 1.1)

Setting MCMC Options

1. As convergence is assessed using multiple chains, more than one should be run
   1. Between-chain variance estimates improve with the number of chains, so I typically use four chains
   2. Other than two; more than one should work
2. Warmup/burnin period should be long enough to ensure chains move to center of posterior distribution
   1. Difficult to determine ahead of time
   2. More complex models need more warmup/burnin to converge
3. Sampling iterations should be long enough to thoroughly sample posterior distribution
   1. Difficulty to determine ahead of time
   2. Need smooth densities across bulk posterior
4. Often, multiple analyses (with different settings) is what is needed

The Markov Chain Traceplot

DietDataExample.R

bayesplot::mcmc_trace(model00.samples$draws("beta0"))

The Posterior Distribution

DietDataExample.R

bayesplot::mcmc_dens(model00.samples$draws("beta0"))

Assessing Our Chains

DietDataExample.R

model00.samples$summary()

# A tibble: 63 × 10
   variable        mean median    sd   mad     q5    q95  rhat ess_bulk ess_tail
   <chr>          <dbl>  <dbl> <dbl> <dbl>  <dbl>  <dbl> <dbl>    <dbl>    <dbl>
 1 lp__          -129.  -128.   1.02 0.728 -131.  -128.   1.00   17463.   22953.
 2 beta0          171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
 3 sigma           51.8   51.1  7.20 6.90    41.5   64.8  1.00   27684.   24226.
 4 weightLB_pre…  171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
 5 weightLB_pre…  171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
 6 weightLB_pre…  171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
 7 weightLB_pre…  171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
 8 weightLB_pre…  171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
 9 weightLB_pre…  171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
10 weightLB_pre…  171.   171.   9.54 9.26   155.   186.   1.00   30439.   23880.
# ℹ 53 more rows

• The summary() function reports the PSRF (also known as rhat)

• Here we look at two parameters: \(\beta_0\) and \(\sigma\)

  • Both have $\(\hat{R} = 1.00\), so both are converged

  • lp__ is so-called posterior log-likelihood, does not necessarily need examined, but may be used for model comparison

  • ess columns show effect sample size for chains (factoring in autocorrelation between correlations)

    • More is better

Results Interpretation: Part I

• At long last, with a set of converged Markov chains, we can now interpret the results

  • Here, we disregard which chain samples came from and pool all sampled values to results

• We use summaries of posterior distributions when describing model parameters

  • Typical summary: the posterior mean

    • The mean of the sampled values in the chain

  • Called EAP (Expected a Posteriori) estimates

  • Less common: posterior median

• Important point:

  • Posterior means are different than what characterizes the ML estimates

    • Analogous to ML estimates would be the mode of the posterior distribution

  • Especially important if looking at non-symmetric posterior distribution

    • Look at posterior for variances

Results Interpretation: Part II

• To summarize the uncertainty in parameters, the posterior SD is used

  • The standard deviation of the sampled values in the all chains

  • The is the analogous to the standard error from ML

• Bayesian credible intervals are formed by taking quantiles of the posterior distribution

  • Analogous to confidence intervals

  • Interpretation slightly different - the probability the parameter lies within the interval

  • 95% credible interval nodes that parameter is within interval with 95% confidence

• Additionally, highest density posterior intervals can be formed

  • The narrowest range for an interval (for unimodal posterior distributions)

90% and 95% Credible Interval

quantile(model00.samples$draws('beta0'), c(.05, .95))

      5%      95% 
155.2948 186.4850 

quantile(model00.samples$draws('beta0'), c(.025, .975))

    2.5%    97.5% 
152.0660 189.8721 

bayesplot::mcmc_dens(model00.samples$draws('beta0')) +
  geom_vline(xintercept = quantile(model00.samples$draws('beta0'), c(.025, .975)), col = "red", size = 1.2) +
  geom_vline(xintercept = quantile(model00.samples$draws('beta0'), c(.05, .95)), col = "green", size = 1.2)

quantile(model00.samples$draws('sigma'), c(.05, .95))

      5%      95% 
41.53700 64.82484 

quantile(model00.samples$draws('sigma'), c(.025, .975))

    2.5%    97.5% 
40.08569 68.21151 

bayesplot::mcmc_dens(model00.samples$draws('sigma')) +
  geom_vline(xintercept = quantile(model00.samples$draws('sigma'), c(.025, .975)), col = "red", size = 1.2) +
  geom_vline(xintercept = quantile(model00.samples$draws('sigma'), c(.05, .95)), col = "green", size = 1.2)

Using rstanarm for simple Bayesian models

library(rstanarm)
# Set this manually if desired:
ncores <- parallel::detectCores(logical = FALSE)
###
options(mc.cores = ncores)
set.seed(5078022)
refm_fit <- stan_glm(
  WeightLB ~ 1,
  family = gaussian(),
  data = dat,
  ### 5000 warmups and 5000 samplings
  chains = 4, iter = 10000
)
summary(refm_fit)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      WeightLB ~ 1
 algorithm:    sampling
 sample:       20000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 30
 predictors:   1

Estimates:
              mean   sd    10%   50%   90%
(Intercept) 171.0    9.3 159.2 170.9 182.8
sigma        50.8    6.9  42.6  50.1  59.9

Fit Diagnostics:
           mean   sd    10%   50%   90%
mean_PPD 171.0   13.3 154.1 171.1 187.9

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
              mcse Rhat n_eff
(Intercept)   0.1  1.0  12322
sigma         0.1  1.0  11327
mean_PPD      0.1  1.0  14789
log-posterior 0.0  1.0   7153

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Wrapping up

1. MCMC algorithm includes the Bayes’ theorm and sampling approaches
2. Stan syntax: need .stan storing the model information and .r storing R codes to run and summarize the model
3. cmdstanr will compile the .stan and run the MCMC
4. To run MCMC, you need to specify number of chains, interations, burnins. You also translate data information into a data list
5. After you finish estimation, check the convergence using \(\hat{R}\) and visual inspection of traceplot