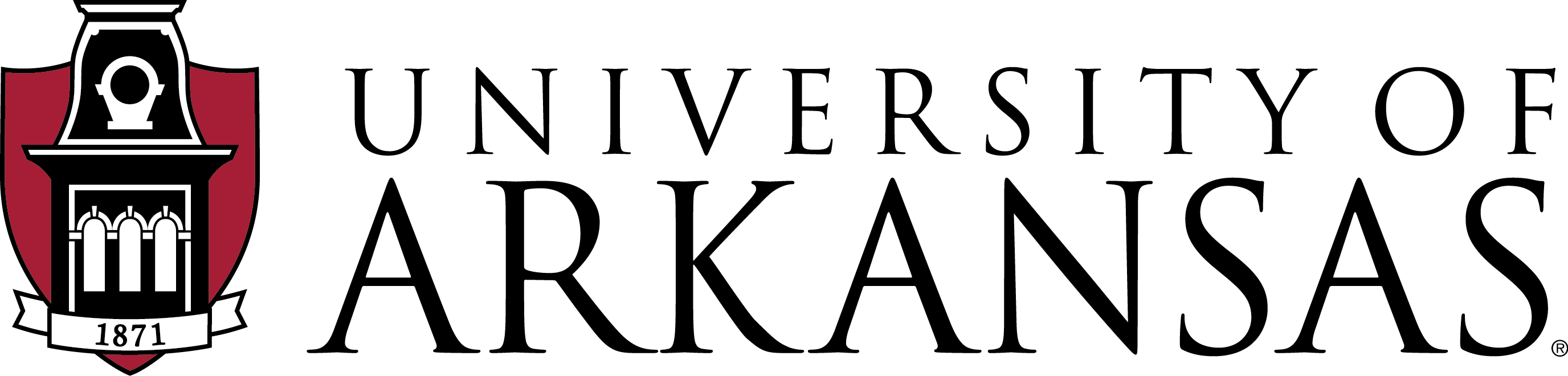Lecture 06

Generalized Measurement Models: An Introduction

Jihong Zhang

Educational Statistics and Research Methods

Today’s Lecture Objectives

Introduce measurement (psychometric) models in general
Describe the steps needed in a psychometric model analysis
Dive deeper into the observed-variables modeling aspect

Measurement Model in general

Measurement Model Analysis Steps

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph TD
subgraph "Measurement Procedure"
  subgraph Modeling
  direction LR
  Start --> id1
  id1([Specify model]) --> id2(["`Specify scale identification 
  method for latent variables`"])
  id2 --> id3([Estimate model])
  id3 --> id4{Adequate fit indices}
  id4 -- No --> id1
  end
  Modeling -- Model fit acceptable --> one
  subgraph one["Evaluation: Measurement Model with Auxiliary Components"]
    direction LR
    id5(["Score estimation 
    and secondary analyses with scores"]) --> id6([Item evaluation])
    id6 --> id7([Scale construction])
    id7 --> id8([Equating])
    id8 --> id9([Measure Invariance/Differential item functioning])
    id9 --> End
  end
end
style Start fill:#f9f,stroke:#333,stroke-width:5px
style End fill:#bbf,stroke:#333,stroke-width:5px

Components of a Measurement Model

There are two components of a measurement model

Theory (what we cannot see but assume its existence):

Latent variable(s)
Other effects as needed by a model
- Random effects (e.g., initial status and slopes in Latent Growth Model)
- Testlet effects (e.g., a group-level variation among items)
- Effects of observed variables (e.g., gender differences, DIF, Measurement Invariance)

Data (what we can see and we assume generated by theory):

Outcomes
- An assumed distribution for each outcome
- A key statistic of outcome for the model (e.g., mean, sd)
- A link function

General form for measurement model (SEM, IRT):

\[ f(E(\mathbf{Y}\mid\Theta)) = \boldsymbol{\mu} +\Theta\Lambda^T \]

and

\[ \Lambda_j = Q \odot \boldsymbol{\lambda_j} \]

Assume N as sample size, P as number of factors, J as number of items. Then,

$f()$: link function. CFA: identity link; IRT: logistic/probit link
$E(\mathbf{Y}\mid\Theta)$: Expected/Predicted values of outcomes
$\Theta$: latent factor scores matrix (N $\times$ P)
$\Lambda$: A factor loading matrix (J $\times$ P)
- $\Lambda_j$: $j$th row vector of factor loading matrix
- $\textbf{Q}$: Q-matrix represents the connections between items and latent variables
- $\boldsymbol{\lambda}_j$: a vector of factor loading vectors for item $j$
$\mu$: item intercepts (J $\times$ 1)

Example 1 with general form

Let’s consider a measurement model with only one latent variable and five items:

%%{init: {"flowchart": {"htmlLabels": false}} }%%
flowchart TD
  id1((θ)) --> id2["Y1"]
  id1 --> id3["Y2"]
  id1 --> id4["Y3"]
  id1 --> id5["Y4"]
  id1 --> id6["Y5"]

The model shows:

One latent variable ($\theta$)
Five observed variables ($\mathbf{Y} = \{Y_1, Y_2, Y_3, Y_4, Y_5\}$)

Then,

$\Theta$ = $\begin{bmatrix} \theta_1, \\\theta_2,\\ \cdots,\\ \theta_N \end{bmatrix}$
$\Lambda^T$ = $\begin{bmatrix}\lambda_1, \lambda_2, ..., \lambda_5 \end{bmatrix}$

Example 2 with general form

Let’s consider a measurement model with only two latent variables and five items:

%%{init: {"flowchart": {"htmlLabels": false}} }%%
flowchart TD
  theta1((θ1)) --> id2["Y1"]
  theta1 --> id3["Y2"]
  theta1 --> id4["Y3"]
  theta1 --> id5["Y4"]
  theta1 --> id6["Y5"]
  theta2((θ2)) --> id2["Y1"]
  theta2 --> id3["Y2"]
  theta2 --> id4["Y3"]
  theta2 --> id5["Y4"]
  theta2 --> id6["Y5"]

The model shows:

Two latent variables ($\theta_1$, $\theta_2$)
Five observed variables ($\mathbf{Y} = \{Y_1, Y_2, Y_3, Y_4, Y_5\}$)

Then,

$\Theta$ = $\begin{bmatrix} \theta_{1,1}, \theta_{1,2}\\\theta_{2,1}, \theta_{2,2}\\ \cdots,\cdots \\ \theta_{N, 1}, \theta_{N,2} \end{bmatrix}$ $\sim [0, \Sigma]$
$\Lambda^T$ = $\begin{bmatrix}\lambda_{1,1}, \lambda_{1,2}, ..., \lambda_{1,5}\\\lambda_{2,1}, \lambda_{2,2}, ..., \lambda_{2,5}\end{bmatrix}$

Example 3 with general form

Let’s consider a measurement model with only two latent variables and five items:

%%{init: {"flowchart": {"htmlLabels": false}} }%%
flowchart TD
  theta1((θ1)) --> id2["Y1"]
  theta1 --> id3["Y2"]
  theta1 --> id4["Y3"]
  theta2((θ2)) --> id4["Y3"]
  theta2 --> id5["Y4"]
  theta2 --> id6["Y5"]

The model shows:

Two latent variables ($\theta_1$, $\theta_2$)
Five observed variables ($\mathbf{Y} = \{Y_1, Y_2, Y_3, Y_4, Y_5\}$)

Then,

$\Theta$ = $\begin{bmatrix} \theta_{1,1}, \theta_{1,2}\\\theta_{2,1}, \theta_{2,2}\\ \cdots,\cdots \\ \theta_{N, 1}, \theta_{N,2} \end{bmatrix}$ $\sim [0, \Sigma]$
$\Lambda^T$ = $\begin{bmatrix}\lambda_{1,1}, \lambda_{1,2}, \lambda_{1,3}, 0,0\\ 0, 0, \lambda_{2,3}, \lambda_{2,4}, \lambda_{2,5}\end{bmatrix}$
Note that we only limit our model to main-effect models. Interaction effects of factors introduce more complexity.
It is difficulty to specify factor loadings with $0$s directly

Item-specific form

For each item j:

\[ \mathbf{Y_j} \sim N(\mu_j+ \boldsymbol{\lambda}_{j}Q_j\Theta, \psi_j) \]

Bayesian view: latent variables

Latent variables in Bayesian are built by following specification:

What are their distributions? (normal distribution or others)
- For example, $\theta_i$ values for one person and $\theta$ values for samples. Factor score $\theta$ is a mixture distribution of distributions of each individual’s factor score $\theta_i$
- But, in MLE/WSLMV, we do not estimate mean and sd of each individual’s factor score for model to be converged

Code

library(tidyverse)
set.seed(12)
N = 15
ndraws = 200
FS = matrix(NA, nrow = N, ndraws)
FS_p = rnorm(N)
FS_p = FS_p[order(FS_p)]
for (i in 1:N) {
  FS[i,] = rnorm(ndraws, mean = FS_p[i], sd = 1)
}
FS_plot <- as.data.frame(t(FS))
colnames(FS_plot) <- paste0("Person", 1:N)
FS_plot <- FS_plot |> pivot_longer(everything(), names_to = "Person", values_to = "Factor Score")
FS_plot$Person <- factor(FS_plot$Person, levels = paste0("Person", 1:N))
ggplot() +
  geom_density(aes(x = `Factor Score`, fill = Person, col = Person ), alpha = .5, data = FS_plot)  +
  geom_density(aes(x = FS_p))

Multidimensionality
- How many factors to be measured?
- If $\geq$ 2 factors, we specify mean vectors and variance-covariance matrix
- To link latent variables with observed variables, we need to create a indicator matrix of coefficient/effects of latent variable on items.
  - In diagnostic modeling and multidimensional IRT, we call it Q-matrix

Simulation Study 1

Let’s perform a small simulation study to see how to perform factor analysis in naive Stan.
The model specification is a two-factor with each measured by 3 items. In total, there are 6 items with continuous responses. Sample size is 1000.

Model Specification

Data Simulation

set.seed(1234)
N <- 1000
J <- 6
# parameters
psi <- .3 # factor correlation
sigma <- .1 # residual varaince
FS <- mvtnorm::rmvnorm(N, mean = c(0, 0), sigma = matrix(c(1, psi, psi, 1), 2, 2, byrow = T))
Lambda <- matrix(
  c(
    0.7, 0,
    0.5, 0,
    0.3, 0,
    0, 0.7,
    0, 0.5,
    0, 0.3
  ), 6, 2,
  byrow = T
)
mu <- matrix(rep(0.1, J), nrow = 1, byrow = T)
residual <- mvtnorm::rmvnorm(N, mean = rep(0, J), sigma = diag(sigma^2, J))
Y <- t(apply(FS %*% t(Lambda), 1, \(x) x + mu)) + residual
Q <- matrix(
  c(
    1, 0,
    1, 0,
    1, 0,
    0, 1,
    0, 1,
    0, 1
  ), 6, 2,
  byrow = T
)
loc <- Q |>
  as.data.frame() |>
  rename(`1` = V1, `2` = V2) |> 
  rownames_to_column("Item") |>
  pivot_longer(c(`1`, `2`), names_to = "Theta", values_to = "q") |> 
  mutate(across(Item:q, as.numeric)) |> 
  filter(q == 1) |> 
  as.matrix()

head(Y)

           [,1]        [,2]         [,3]       [,4]        [,5]        [,6]
[1,] -0.8030701 -0.48545470 -0.256368448  0.2829436 -0.02007136  0.02274601
[2,]  0.4271083  0.50926367  0.270175274 -1.5916892 -1.05896321 -0.64570802
[3,]  0.4803976  0.40621781  0.122951997  0.5982296  0.42932001  0.29298711
[4,] -0.3292829 -0.18227739  0.002010588 -0.3921847 -0.20918407  0.19121259
[5,] -0.4938891 -0.21694927 -0.251691793 -0.5544642 -0.28519849 -0.42496295
[6,] -0.3946768  0.01379814 -0.164355671 -0.7838352 -0.38385332 -0.29007225

Strategies for Stan: factor loadings

We will iterate over item response function across each item
To benefit from the efficiency of vectorization, we specify a vector of factor loadings with length 6
- $\{\lambda_1, \lambda_2, \cdots, \lambda_6 \}$
- Optionally, a matrix with number of items by number of factor for $\lambda$s can be specified like $\lambda_{11}$ and $\lambda_{62}$, that introduces flexibility but complexity
We should have a location table telling stan the information about which factor each factor loading belong to
- For example, $\lambda_{1}$ belongs to factor 1 and $\lambda_4$ belong to factor 2

loc

     Item Theta q
[1,]    1     1 1
[2,]    2     1 1
[3,]    3     1 1
[4,]    4     2 1
[5,]    5     2 1
[6,]    6     2 1

Strategies for Stan: prior distribution and hyperparameters

residual variances for items: $\sigma \sim \text{exponential}(sigmaRate)$
- sigmaRate is set to 1
item intercepts: $\mu \sim \text{MVN}(meanMu, covMu)$
- meanMu is set to a vector of 0s with length 6
- covMu is set to a diagonol matrix of 1000 with 6 $\times$ 6
factor scores: $\Theta \sim \text{MVN}(meanTheta, corrTheta)$
- meanTheta is set to a vector of 0s with length 2
- $corrTheta \sim lkj\_corr(eta)$ and eta is set to 1
- Optionally, $L \sim lkj\_corr\_cholesky(eta)$ and corrTheta = LL’
factor loadings: $\Lambda \sim \text{MVN}(meanLambda, covLambda)$
- meanLambda is set to a vector of 0s with length 6 (number of items)
- covLambdais set to a matrix of $\begin{pmatrix}1000, 0,\cdots,0\\ \cdots\\0, 0, \cdots1000\end{pmatrix}$

Question: what about factor correlation $\psi$?
See this blog and Stan’s reference for Choleskey decomposition
For eta = 1, the distribution is uniform over the space of all correlation matrices

Data Structure and Data Block

Lecture06.R

data_list <- list(
  N = 1000, # number of subjects/observations
  J = J, # number of items
  K = 2, # number of latent variables,
  Y = Y,
  Q = Q,
  # location/index of lambda
  kk = loc[,2],
  #hyperparameter
  sigmaRate = .01,
  meanMu = rep(0, J),
  covMu = diag(1000, J),
  meanTheta = rep(0, 2),
  eta = 1,
  meanLambda = rep(0, J),
  covLambda = diag(1000, J)
)

simulation_loc.stan

data {
  int<lower=0> N; // number of observations
  int<lower=0> J; // number of items
  int<lower=0> K; // number of latent variables
  matrix[N, J] Y; // item responses
  
  //location/index of lambda
  array[J] int<lower=0> kk;
  
  //hyperparameter
  real<lower=0> sigmaRate;
  vector[J] meanMu;
  matrix[J, J] covMu;      // prior covariance matrix for coefficients
  vector[K] meanTheta;
  
  vector[J] meanLambda;
  matrix[J, J] covLambda;      // prior covariance matrix for coefficients
  
  real<lower=0> eta; // LKJ shape parameters
}

Parameter and Transformed Parameter block

simulation_loc.stan

parameters {
  vector[J] mu;                      // item intercepts
  vector<lower=0,upper=1>[J] lambda; // factor loadings
  vector<lower=0>[J] sigma;          // the unique residual standard deviation for each item
  matrix[N, K] theta;                // the latent variables (one for each person)
  cholesky_factor_corr[K] L;         // L of factor correlation matrix
}
transformed parameters{
  matrix[K,K] corrTheta = multiply_lower_tri_self_transpose(L);
}

Note that L is the Cholesky decomposition factor of factor correlation matrix

It is also a lower triangle matrix
use cholesky_factor_corr[K] to declare this parameter
Sometime, parameters are those that are easy to sampling, transformed parameters block is used to transform your parameters to those that are difficulty to direct sampling.

Model block

Lecture06.R

data_list <- list(
  N = 1000, # number of subjects/observations
  J = J, # number of items
  K = 2, # number of latent variables,
  Y = Y,
  Q = Q,
  # location/index of lambda
  kk = loc[,2],
  #hyperparameter
  sigmaRate = .01,
  meanMu = rep(0, J),
  covMu = diag(1000, J),
  meanTheta = rep(0, 2),
  eta = 1,
  meanLambda = rep(0, J),
  covLambda = diag(1000, J)
)

simulation_loc.stan

model {
  mu ~ multi_normal(meanMu, covMu);
  sigma ~ exponential(sigmaRate);   
  lambda ~ multi_normal(meanLambda, covLambda);
  L ~ lkj_corr_cholesky(eta);
  for (i in 1:N) {
    theta[i,] ~ multi_normal(meanTheta, corrTheta);
  }
  for (j in 1:J) { // loop over each item response function
    Y[,j] ~ normal(mu[j]+lambda[j]*theta[,kk[j]], sigma[j]);
  }
}

Note that kk[j] selects which factor to be multiplied dependent on factor loading’s index. That why we have a location matrix of factor loadings. Theta in loc table is kk.

loc

     Item Theta q
[1,]    1     1 1
[2,]    2     1 1
[3,]    3     1 1
[4,]    4     2 1
[5,]    5     2 1
[6,]    6     2 1

Generated quantities block

simulation_loc.stan

generated quantities {
  vector[N * J] log_lik;
  matrix[N, J] temp;
  matrix[N, J] Y_rep;
  vector[J] Item_Mean_rep;
  for (i in 1:N) {
    for (j in 1:J) {
      temp[i, j] = normal_lpdf(Y[i, j] | mu[j]+lambda[j]*theta[i,kk[j]],  sigma[j]); 
    }
  }
  log_lik = to_vector(temp);
  for (j in 1:J) {
    Y_rep[,j] = to_vector(normal_rng(mu[j]+lambda[j]*theta[,kk[j]], sigma[j]));
    Item_Mean_rep[j] = mean(Y_rep[,j]);
  }
}

To obtain leave-one-out (LOO) model fitting, we need to generate log-likelihood:

log_lik includes both person information and item information in factor analysis and IRT
log_lik must be a vector in Stan
Thus, the length of log-likelihood is a vector of length N $\times$ J

To conduct posterior predictive model checking, we need to generate simulation data sets: Y_rep

Y_rep can be generated using normal_rng and posterior draws of parameters
Item_Mean_rep were generated to compared to observed item means

Model Estimation

Here, my MCMC estimation is set to:

Four MCMC chains that are running parallel
A seed as 1234 for replication
The warmup iteration is 1000 and the sampling iteration is 2000. Thus, the total iteration is 3000.
Since we have 4 chains, the total iteration for summary statistics is 12000 iterations.
The total estimation time is 220s (3.6 minutes)

#| eval: false
mod_cfa_twofactor <- cmdstan_model(here::here("posts", "Lectures", "2024-01-12-syllabus-adv-multivariate-esrm-6553", "Lecture06", "Code", "simulation_loc.stan"))
fit_cfa_twofactor <- mod_cfa_twofactor$sample(
  data = data_list,
  seed = 1234,
  chains = 4,
  parallel_chains = 4, 
  iter_sampling = 2000,
  iter_warmup = 1000
)

fit_cfa_twofactor$time()

MCMC Result > Model diagnostic > PPMC

All items have PPP of item mean close to 0.5, suggesting great model-data fitting.

Item_Mean_rep_mat <- fit_cfa_twofactor$draws("Item_Mean_rep", format = 'matrix')
Item_Mean_obs <- colMeans(Y)
PPP <- rep(NA, J)
# colMeans(Item_Mean_rep_mat)
for (item in 1:J) {
  PPP[item] <- mean(as.numeric(Item_Mean_rep_mat[,item]) > Item_Mean_obs[item])
}
PPP
data.frame(
  Item = factor(1:J, levels = 1:J),
  PPP = PPP
) |> 
  ggplot() +
  geom_col(aes(x = Item, y = PPP)) + 
  geom_hline(aes(yintercept = .5), col = 'red', size = 1.3) + 
  theme_classic()

Posterior predictive distribution of item means

obs_mean <- data.frame(
  Item = paste0("Item_Mean_rep[", 1:6,"]"),
  y = Item_Mean_obs
)
Item_Mean_rep_mat |> as.data.frame() |> 
  pivot_longer(everything(), names_to = "Item", values_to = "Posterior") |> 
  ggplot() +
  geom_density(aes(x = Posterior)) +
  geom_vline(aes(xintercept = y), data = obs_mean, col ='red') +
  facet_wrap(~ Item, scales = "free")

MCMC Result > Model diagnostic > LOO

We firt examined the max/mean PSRF (rhat) for convergence. This is also called Gelman and Rubin diagnosis. The maximum RSRF is 1.03 suggesting MCMC estimation converged.

Then, we examined the LOO with PSIS. According to Pareto K diagnostic, most log-likelihood estimation suggests good reliability.

Question: Why we have 8000 $\times$ 6000 log-likelihood elements? hints: our information in data

fit_cfa_twofactor$summary(
  variables = NULL,
  "rhat"
) |> 
 summarise(mean_rhat = mean(rhat, na.rm = T),
           max_rhat = max(rhat, na.rm = T))

loo_res <- fit_cfa_twofactor$loo(variables = 'log_lik', save_psis = TRUE, cores = 2)
print(loo_res)

MCMC Results > Estimation > Factor Loadings

Benchmark model using lavaan

# lavaan
mod <- "
F1 =~ I1 + I2 + I3
F2 =~ I4 + I5 + I6
"
dat <- as.data.frame(Y)
colnames(dat) <- paste0('I', 1:6)
fit <- cfa(mod, data = dat, std.lv = TRUE)
lavaan::parameterestimates(fit) |> filter(op == "=~")

  lhs op rhs   est    se      z pvalue ci.lower ci.upper
1  F1 =~  I1 0.720 0.016 43.685      0    0.688    0.752
2  F1 =~  I2 0.514 0.012 43.082      0    0.491    0.538
3  F1 =~  I3 0.310 0.008 40.922      0    0.295    0.325
4  F2 =~  I4 0.673 0.015 43.699      0    0.643    0.703
5  F2 =~  I5 0.483 0.011 42.975      0    0.461    0.505
6  F2 =~  I6 0.293 0.007 40.248      0    0.279    0.307

Model 1 using Stan

fit_cfa_twofactor$summary("lambda") |> select(variable,mean, median, sd, q5, q95)

fit_cfa_twofactor$summary("lambda", \(x) quantile(x, c(.025, .975)))

We can easily notice how consistent between estimates of lavaan with Stan :

est in lavaan corresponds to mean or median in stan . Their difference is around .001 - .002.
se in lavaan corresponds to sd in stan
ci.lower and ci.upper in lavaan is for 95% confidence interval, so they have larger range than q5 and q95 in Stan, which is for 90% Credible Interval
90% CI is the default setting, but we can calculate Bayesian 95% Credible Interval using $summary()

MCMC Results > Visualization > Factor Loadings

bayesplot::color_scheme_set("viridis")
bayesplot::mcmc_trace(fit_cfa_twofactor$draws(), regex_pars = "lambda")

MCMC Results > Estimation > Factor Correlation

The factor correlation (Psi = .3) is represented by the non-diagonal elements of factor correlation.

There are two ways to check estimation of factor correlation:

Since we use LKJ sampling with L Cholesky factor, recall that L is lower triangle of factor correlation.

fit_cfa_twofactor$summary("L[2,1]")

We can also look at the elements of factor correlation matrix

fit_cfa_twofactor$summary(c("corrTheta[1,2]", "corrTheta[2,1]"))

MCMC Results > Visualization > Factor Correlation

We can also visual inspect trace plots of MCMC draws of L
What type of error leads to the deviation between posterior values of L and true value.

bayesplot::mcmc_trace(fit_cfa_twofactor$draws("L[2,1]"))

MCMC Results > Estimation > Item Intercepts

Item intercepts are set to .1. Let’s see what Bayesian model recovers the true values

fit_cfa_twofactor$summary("mu")

We notices item 4 is little off with true values.

bayesplot::mcmc_trace(fit_cfa_twofactor$draws("mu"))

MCMC Results > Estimation > Residual variances

fit_cfa_twofactor$summary("sigma")

bayesplot::mcmc_trace(fit_cfa_twofactor$draws("sigma"))

Simulation Study 2

To illustrate how to model a more complex CFA with cross-loadings, let’s generate a new simulation data with test length 7 and two latent variables
The mean structure of model is like this, each latent variable was measured by 4 items. The other parameters are as same as Model 1.

Mean Structure of Model 2

Strategies for Model 2

The general idea is that we assign a uninformative prior distribution for “main” factor loadings, and assign informative “close-to-zero” prior distribution for “zero” factor loadings:

Strategies for Model 2 (Cont.)

Have a more detailed location matrix for factor loading matrix

as.data.frame(Lambda2)

   V1  V2
1 0.7 0.0
2 0.5 0.0
3 0.3 0.0
4 0.5 0.5
5 0.0 0.7
6 0.0 0.5
7 0.0 0.3

We can transform the information of factor loading into:

## Transform Q to location index
loc2 <- Q2 |>
  as.data.frame() |>
  rename(`1` = V1, `2` = V2) |> 
  rownames_to_column("Item") |>
  pivot_longer(c(`1`, `2`), names_to = "Theta", values_to = "q") |> 
  mutate(across(Item:q, as.numeric)) |> 
  mutate(q = -q + 2) |> 
  as.matrix()
as.data.frame(loc2)

   Item Theta q
1     1     1 1
2     1     2 2
3     2     1 1
4     2     2 2
5     3     1 1
6     3     2 2
7     4     1 1
8     4     2 1
9     5     1 2
10    5     2 1
11    6     1 2
12    6     2 1
13    7     1 2
14    7     2 1

Where Item represents the index of item a factor loading belongs to, and Theta represents the index of latent variables a factor loading belongs to.
In Stan’s data block, we denote Item of location matrix as jj and Theta as kk . q represents two types of prior distributions for factor loadings.

simulation_exp2.stan

data {
  ...
  int<lower=0> R; // number of rows in location matrix
  array[R] int<lower=0>jj;
  array[R] int<lower=0>kk;
  array[R] int<lower=0>q;
  ...
}

Data Structure and Data Block

Lecture06.R

data_list2 <- list(
  N = 1000, # number of subjects/observations
  J = J2, # number of items
  K = 2, # number of latent variables,
  Y = Y2,
  Q = Q2,
  # location of lambda
  R = nrow(loc2),
  jj = loc2[,1],
  kk = loc2[,2],
  q = loc2[,3],
  #hyperparameter
  meanSigma = .1,
  scaleSigma = 1,
  meanMu = rep(0, J2),
  covMu = diag(10, J2),
  meanTheta = rep(0, 2),
  corrTheta = matrix(c(1, .3, .3, 1), 2, 2, byrow = T)
)

simulation_exp2.stan

data {
  int<lower=0> N; // number of observations
  int<lower=0> J; // number of items
  int<lower=0> K; // number of latent variables
  matrix[N, J] Y; // item responses
  
  int<lower=0> R; // number of rows in location matrix
  array[R] int<lower=0>jj;
  array[R] int<lower=0>kk;
  array[R] int<lower=0>q;
  
  //hyperparameter
  real<lower=0> meanSigma;
  real<lower=0> scaleSigma;
  vector[J] meanMu;
  matrix[J, J] covMu;      // prior covariance matrix for coefficients
  vector[K] meanTheta;
  matrix[K, K] corrTheta;
  
}

Note that for the simplicity of estimation, I specified the factor correlation matrix as fixed. If you are interested in estimating factor correlation, you can refer to the previous model using LKJ sampling.

Parameters block

simulation_exp2.stan

parameters {
  vector<lower=0,upper=1>[J] mu;
  matrix<lower=0>[J, K] lambda;
  vector<lower=0,upper=1>[J] sigma; // the unique residual standard deviation for each item
  matrix[N, K] theta;                // the latent variables (one for each person)
  //matrix[K, K] corrTheta; // not use corrmatrix to avoid duplicancy of validation
}

For parameters block, the only difference is we specify lambda as a matrix with J $\times$ K, which is 7 $\times$ 2 in our case.

Model block

As you can see, in Model block, we need to use if_else in Stan to specify factor loadings in different locations

For type 1 (green), we specify a uninformative normal distribution
For type 2 (red), we specify a informative shrinkage priors.
For univariate residual, we can simply use cauchy or exponential prior
The item response function estimate each item response using $\mu+ \Lambda * \Theta$ as kernal and $\sigma$ as variation

simulation_exp2.stan

model {
  mu ~ multi_normal(meanMu, covMu);
  // specify lambda's regulation
  for (r in 1:R) {
    if (q[r] == 1){
      lambda[jj[r], kk[r]] ~ normal(0, 10);
    }else{// student_t(nu, mu, sigma)
      lambda[jj[r], kk[r]] ~ student_t(1, 0, 0.01);
    }
  }
  //corrTheta ~ lkj_corr(eta);
  for (i in 1:N) {
    theta[i,] ~ multi_normal(meanTheta, corrTheta);
  }
  for (j in 1:J) {
    sigma[j] ~ cauchy(meanSigma, scaleSigma);                   // Prior for unique standard deviations
    Y[,j] ~ normal(mu[j]+to_row_vector(lambda[j,])*theta', sigma[j]);
  }
}

Model Result > R-hat

We set up the MCMC as follows:

3000 warmups + 3000 samplings = 6000 iterations
Total execution time: 202.7 seconds for my computers but it takes 20 minutes or more if I specify inproper priors
4 chains
R hat is acceptable suggesting convergence

fit_cfa_exp2 <- mod_cfa_exp2$sample(
  data = data_list2,
  seed = 1234,
  chains = 4,
  parallel_chains = 4, 
  iter_sampling = 3000,
  iter_warmup = 3000
)

fit_cfa_exp2$summary(
  variables = NULL,
  "rhat"
) |> 
 summarise(mean_rhat = mean(rhat, na.rm = T),
           max_rhat = max(rhat, na.rm = T))

# A tibble: 1 × 2
  mean_rhat max_rhat
      <dbl>    <dbl>
1      1.00     1.04

MCMC Results > Estimation > Factor Loadings

fit_cfa_exp2$summary('lambda') |> select(variable, mean, median, sd, q5, q95)

# A tibble: 14 × 6
   variable       mean  median      sd       q5    q95
   <chr>         <dbl>   <dbl>   <dbl>    <dbl>  <dbl>
 1 lambda[1,1] 0.714   0.714   0.0164  0.687    0.741 
 2 lambda[2,1] 0.509   0.509   0.0119  0.489    0.529 
 3 lambda[3,1] 0.305   0.305   0.00761 0.293    0.318 
 4 lambda[4,1] 0.515   0.514   0.0130  0.493    0.536 
 5 lambda[5,1] 0.00724 0.00582 0.00597 0.000607 0.0186
 6 lambda[6,1] 0.00795 0.00726 0.00503 0.00128  0.0171
 7 lambda[7,1] 0.00476 0.00422 0.00324 0.000559 0.0107
 8 lambda[1,2] 0.00606 0.00479 0.00523 0.000414 0.0163
 9 lambda[2,2] 0.00797 0.00734 0.00483 0.00142  0.0168
10 lambda[3,2] 0.00618 0.00586 0.00355 0.000989 0.0126
11 lambda[4,2] 0.491   0.491   0.0122  0.471    0.511 
12 lambda[5,2] 0.680   0.680   0.0152  0.655    0.706 
13 lambda[6,2] 0.482   0.482   0.0110  0.464    0.500 
14 lambda[7,2] 0.285   0.285   0.00694 0.274    0.296

Lambda2

     [,1] [,2]
[1,]  0.7  0.0
[2,]  0.5  0.0
[3,]  0.3  0.0
[4,]  0.5  0.5
[5,]  0.0  0.7
[6,]  0.0  0.5
[7,]  0.0  0.3

Wrapping up

We simulated two models: one is 2-factor model without cross-loadings; another is 2-factor model with cross-loadings.

In real setting, the Bayesian modeling could be challenging because

Prior distributions are unsure
Bad prior may leads to unconverge; So try multiple priors
- Good priors will have nice converge very early (i.e, 500 or 1000 samples)
MCMC sampling is computationally intensive, and you may not sure how many iterations are enough
Hard to come up with a strategy of model building
- For example, “location matrix and different priors” is a strategy I prefer
- It may not works for any problems for cross-loadings
You may try blavaan or other wrap-up package for Bayesian CFA, it saves some time for model building
- But you have no idea how they set up MCMC

All of these topics will be with us when we start model complicated models in our future lecture.

Next Class

More strategies about measurement models with Stan

Lecture 06

Today’s Lecture Objectives

Measurement Model in general

Measurement Model Analysis Steps

Components of a Measurement Model

General form for measurement model (SEM, IRT):

Example 1 with general form

Example 2 with general form

Example 3 with general form

Item-specific form

Bayesian view: latent variables

Simulation Study 1

Data Simulation

Strategies for Stan: factor loadings

Strategies for Stan: prior distribution and hyperparameters

Data Structure and Data Block

Parameter and Transformed Parameter block

Model block

Generated quantities block

Model Estimation

MCMC Result > Model diagnostic > PPMC

MCMC Result > Model diagnostic > LOO

MCMC Results > Estimation > Factor Loadings

MCMC Results > Visualization > Factor Loadings

MCMC Results > Estimation > Factor Correlation

MCMC Results > Visualization > Factor Correlation

MCMC Results > Estimation > Item Intercepts

MCMC Results > Estimation > Residual variances

Simulation Study 2

Strategies for Model 2

Strategies for Model 2 (Cont.)

Data Structure and Data Block

Parameters block

Model block

Model Result > R-hat

MCMC Results > Estimation > Factor Loadings

Wrapping up

Next Class

Other materials

Reference