Lecture 02: General Linear Model
Descriptive Statistics and Basic Statistics
Educational Statistics and Research Methods (ESRM) Program*
University of Arkansas
2024-08-26
Some notes before our class
- Vote for delaying class time (to 5:15?) for free parking
- The R code I’ll show in the slides is just for illustration. Don’t be worried about hardly following up. We will practice together at the end of each unit.
Learning Objectives
- Review Homework 0
- Review previous lecture
- Unit 1: Descriptive Statistics
- Introduce R package – ESRM64503
- Univariate Descriptive Statistics
- Central tendency: Mean, Median, Mode
- Variation/Spread: Standard deviation (SD), Variance, Range
- Bivariate descriptive statistics
- Correlation
- Covariance
- Types of variable distributions
- Marginal
- Joint
- Conditional
- Bias in estimators
- Unit 2: General Linear Model
Unit 1: Descriptive Statistics
Homework 0
Question 3
Installation of ESRM64503 package
Test ESTM64503 Package
package * version date (UTC) lib source
ESRM64503 * 2024.08.20 2024-08-20 [1] Github (JihongZ/ESRM64503@ed78e3d)
[1] /Users/jihong/Rlibs
[2] /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/library
There will be four homeworks in total for ESRM 64503.
You can work on HW0 now, please click the following link to have access:
https://jihongzhang.org/posts/Lectures/2024-07-21-applied-multivariate-statistics-esrm64503/HWs/HW_demo.html
Next homework (Homework 1) will be posted on 09/09/2024.
For more details, please refer to
https://jihongzhang.org/posts/Lectures/2024-07-21-applied-multivariate-statistics-esrm64503/Data Files of ESRM64503
id sex heightIN weightLB
1 1 F 56 117
2 2 F 60 125
3 3 F 64 133
4 4 F 68 141
5 5 F 72 149
6 6 F 54 109
7 7 F 62 128
8 8 F 65 131
9 9 F 65 131
10 10 F 70 145
11 11 M 64 211
12 12 M 68 223
13 13 M 72 235
14 14 M 76 247
15 15 M 80 259
16 16 M 62 201
17 17 M 69 228
18 18 M 74 245
19 19 M 75 241
20 20 M 82 269Simulated Data for Today’s Lecture - dataSexHeightWeight
To help demonstrate the concepts of today’s lecture, we will be using a toy data set with three variables
Female (Gender): Coded as Male (= 0) or Female (= 1)
- In R, factor variable with two levels: FALSE, TRUE
Height: in inches
Weight: in pounds
The goal of lecture 02 will be to build a general linear model that predicts a person’s weight
Linear (regression) model: a statistical model for an outcome that uses a linear combination (a weighted sum) of one or more predictor variables to produce an estimate of an observation’s predicted value
\[ \mathbb{y} = \beta_0+\beta_1 \mathbf{X} \]
All models we learnt today will follow this framework.
Recoding Variables
library(ESRM64503) # INSTALL: pak::pak("JihongZ/ESRM64504")
library(kableExtra) # INSTALL: pak::pak("JihongZ/ESRM64504")
## First checking sample size
## N = 20
## Recode Sex as Female
dataSexHeightWeight$female = dataSexHeightWeight$sex == "F"
kable(dataSexHeightWeight,
caption = 'toy data set') |>
kable_styling(font_size = 30)| id | sex | heightIN | weightLB | female |
|---|---|---|---|---|
| 1 | F | 56 | 117 | TRUE |
| 2 | F | 60 | 125 | TRUE |
| 3 | F | 64 | 133 | TRUE |
| 4 | F | 68 | 141 | TRUE |
| 5 | F | 72 | 149 | TRUE |
| 6 | F | 54 | 109 | TRUE |
| 7 | F | 62 | 128 | TRUE |
| 8 | F | 65 | 131 | TRUE |
| 9 | F | 65 | 131 | TRUE |
| 10 | F | 70 | 145 | TRUE |
| 11 | M | 64 | 211 | FALSE |
| 12 | M | 68 | 223 | FALSE |
| 13 | M | 72 | 235 | FALSE |
| 14 | M | 76 | 247 | FALSE |
| 15 | M | 80 | 259 | FALSE |
| 16 | M | 62 | 201 | FALSE |
| 17 | M | 69 | 228 | FALSE |
| 18 | M | 74 | 245 | FALSE |
| 19 | M | 75 | 241 | FALSE |
| 20 | M | 82 | 269 | FALSE |
Descriptive Statistics
First, we can inspect each variable individually (marginal distribution) through a set of descriptive statistics
Visual way: histogram plot or density plot
Statistical way: Central tendency and Variability
Mean, Median, Mode
SD, Range
Second, we can also summarize the joint (bivariate) distribution of two variables through a set of descriptive statistics:
Joint vs. Marginal: joint distribution describes more than one variable simultaneously
Common bivariate descriptive statistics:
- Correlation and covariance
Quick inspection: Missing data rate
- Check (1) if any case has missing value (2) distributions for continuous and categorical variables
FALSE TRUE
1 19 Quick Inspect: Distribution of Categorical Variable
FALSE TRUE
10 10 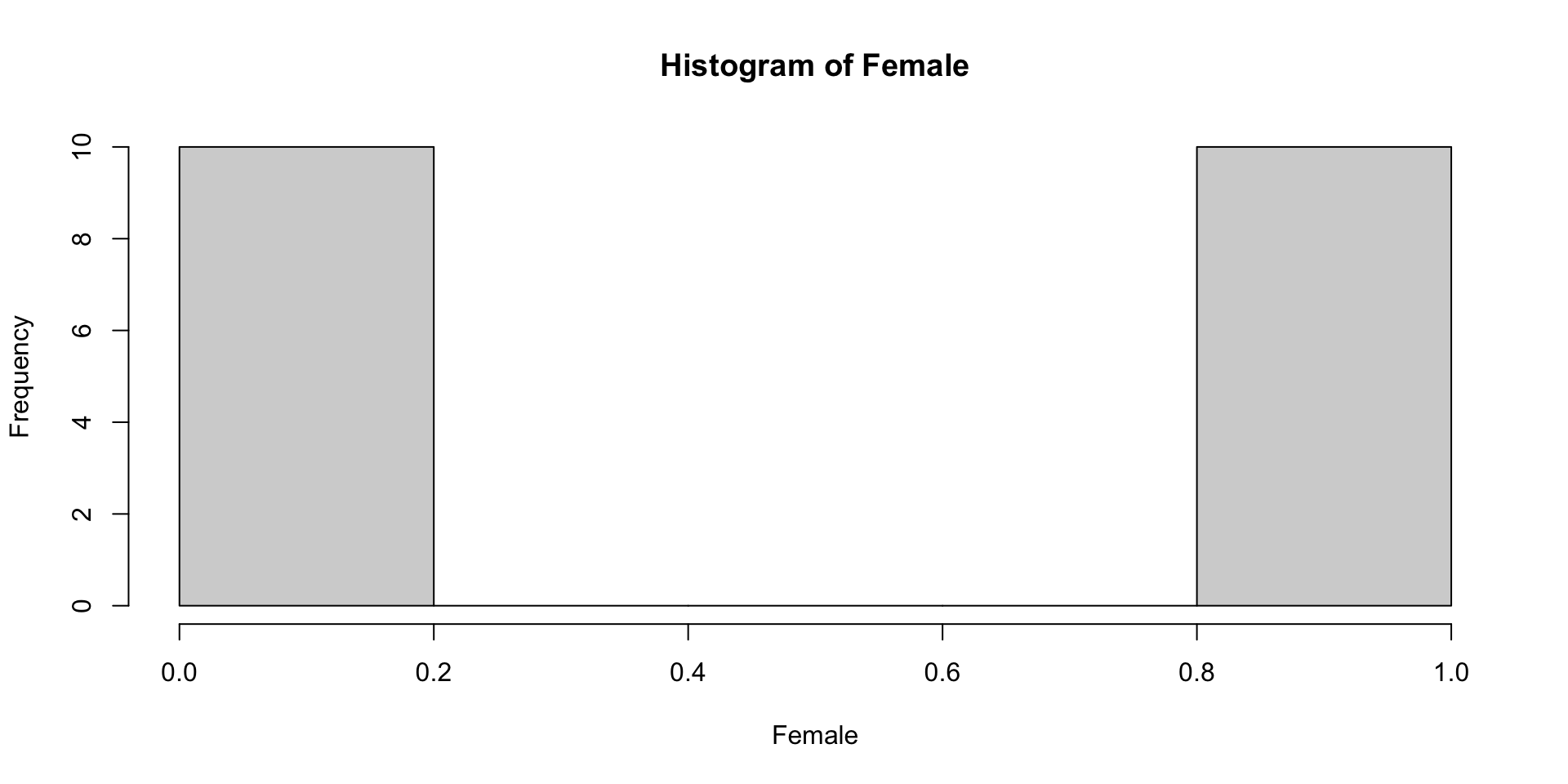
Visualization: Pairwise Scatterplot
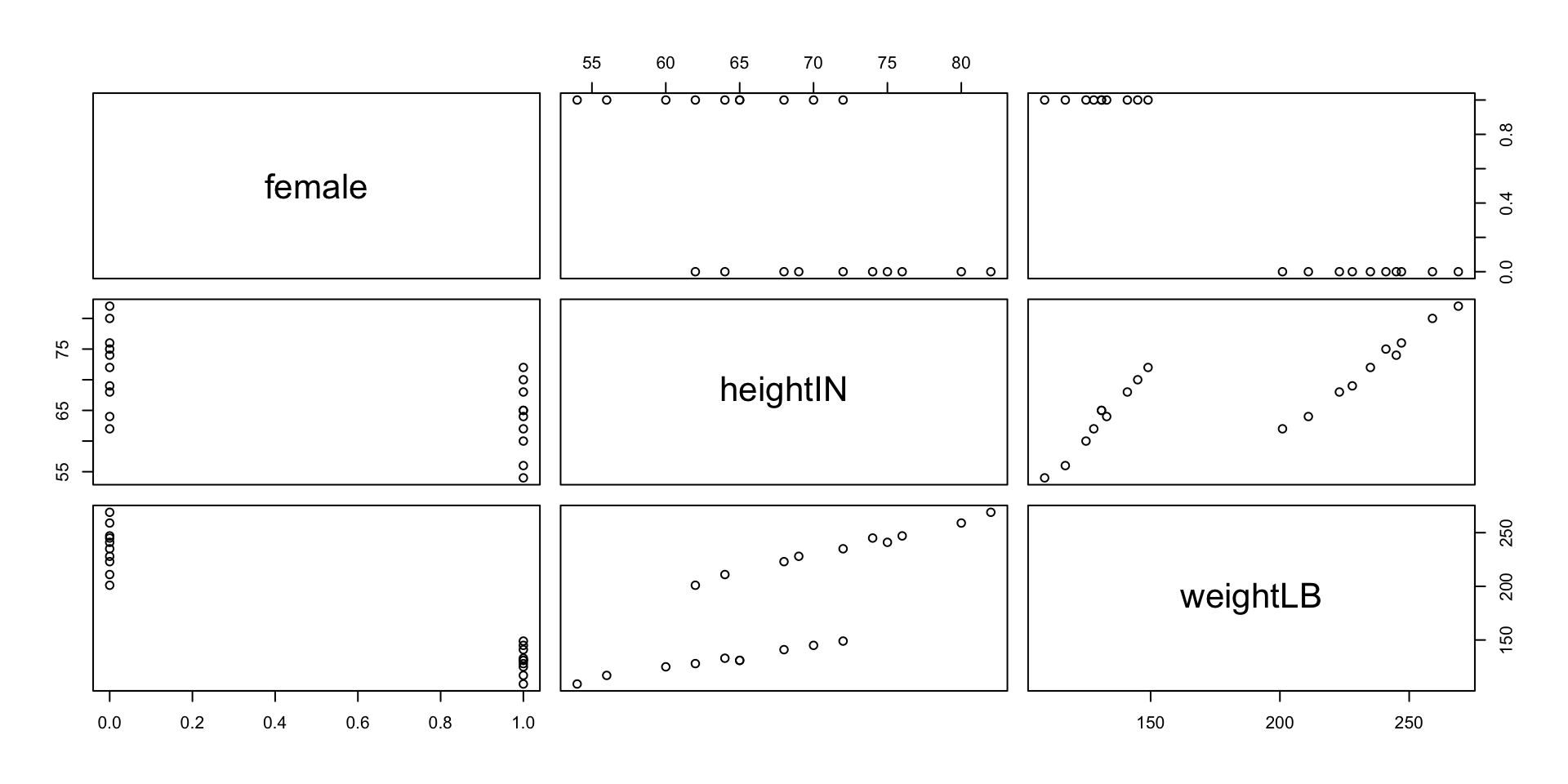
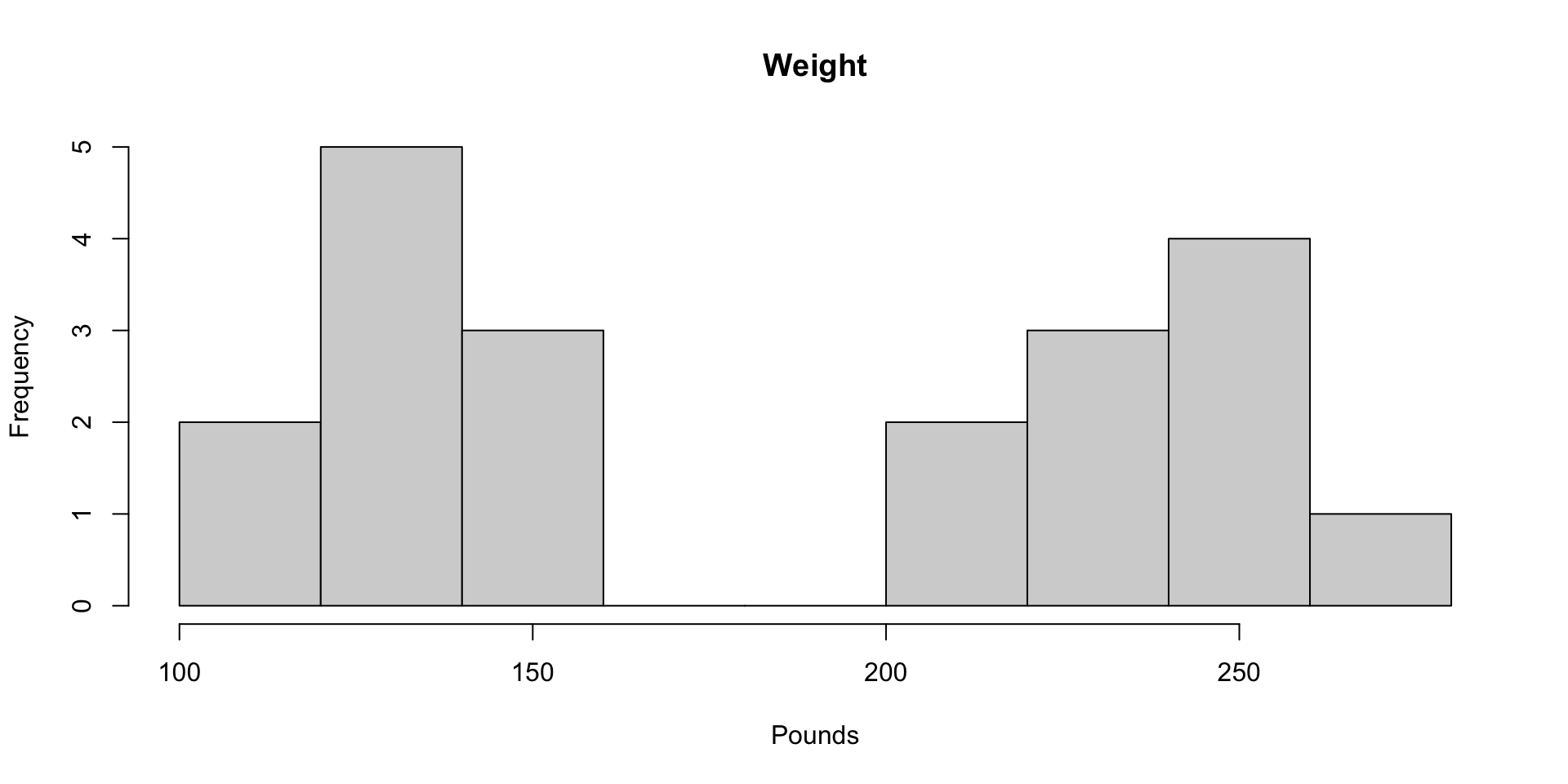
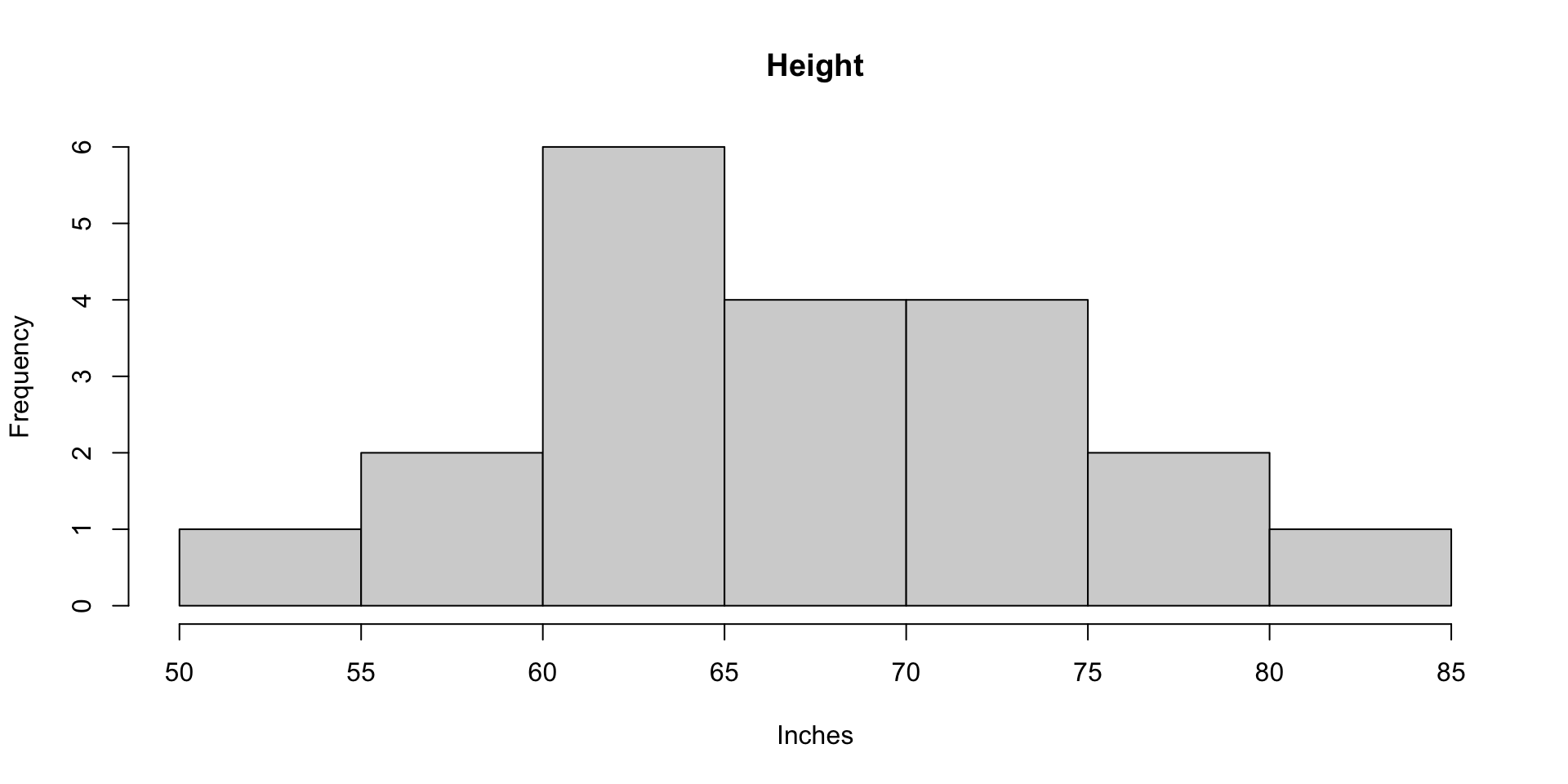
Histograms of Height and Weight
Descriptive Statistics for Toy Data: Marginal
| Variable | mean | sd | var |
|---|---|---|---|
| heightIN | 67.9 | 7.440 | 55.358 |
| weightLB | 183.4 | 56.383 | 3179.095 |
| female | 0.5 | 0.513 | 0.263 |
Descriptive Statistics for Toy Data: Joint
Correlation-Covariance Matrix:
Diagonal: Variance
Above Diagonal (upper triangle): Covaraince
Below Diagonal (lower triangle): Correlation
Question: What we can tell regarding the relationships among three variables?
cor_cov_mat <- matrix(nrow = 3, ncol = 3)
colnames(cor_cov_mat) <- rownames(cor_cov_mat) <- c("heightIN", "weightLB", "female")
cov_mat <- cov(dataSexHeightWeight[, c("heightIN", "weightLB", "female")])
cor_mat <- cor(dataSexHeightWeight[, c("heightIN", "weightLB", "female")])
## Assign values
cor_cov_mat[lower.tri(cor_cov_mat)] <- cor_mat[lower.tri(cor_mat)]
cor_cov_mat[upper.tri(cor_cov_mat)] <- cov_mat[upper.tri(cov_mat)]
diag(cor_cov_mat) <- diag(cov_mat)
kable(cor_cov_mat, digits = 3)| heightIN | weightLB | female | |
|---|---|---|---|
| heightIN | 55.358 | 334.832 | -2.263 |
| weightLB | 0.798 | 3179.095 | -27.632 |
| female | -0.593 | -0.955 | 0.263 |
Variance, Correlation, Covariance
Re-examining the Concept of Variance
Variability is a central concept in advanced statistics
- In multivariate statistic, covariance is also central
Two formulas for the variance (about the same when \(N\) is larger):
\[ S^2_Y= \frac{\Sigma_{p=1}^{N}(Y_p-\bar Y)}{N-1} \qquad(1)\]
\[ S^2_Y= \frac{\Sigma_{p=1}^{N}(Y_p-\bar Y)}{N} \qquad(2)\]
Equation 1: Unbiased or “sample”
Equation 2: Biased/ML or “population”
Here: \(p\) = person;
Biased VS. Unbiased Variability
Code
set.seed(1234)
sample_sizes = seq(10, 200, 10) # N = 10, 20, 30, ..., 200
population_var = 100 # True variance for population
variance_mat <- matrix(NA, nrow = length(sample_sizes), ncol = 4)
iter = 0
for (sample_size in sample_sizes) {
iter = iter + 1
sample_points <- rnorm(n = sample_size, mean = 0, sd = sqrt(population_var))
sample_var_biased <- var(sample_points) * (sample_size-1) / sample_size
sample_var_unbiased <- var(sample_points)
variance_mat[iter, 1] <- sample_size
variance_mat[iter, 2] <- sample_var_biased
variance_mat[iter, 3] <- sample_var_unbiased
variance_mat[iter, 4] <- population_var
}
colnames(variance_mat) <- c(
"sample_size",
"sample_var_biased",
"sample_var_unbiased",
"population_var"
)Take home note: Unbiased variance estimators can get more accurate estimate of variance than the biased one.
Biased VS. Unbiased Estimator of Variance (Cont.)
Code
library(ggplot2)
variance_mat |>
as.data.frame() |>
pivot_longer(-sample_size) |>
ggplot() +
geom_point(aes(x = sample_size, y = value, color = name), linewidth = 1.1) +
geom_line(aes(x = sample_size, y = value, color = name), linewidth = 1.5) +
labs(x = "Sample Size (N)", y = "Estimates of Variance") +
scale_color_manual(values = 1:3, labels = c("Population Variance", "Sample Biased Variance (ML)", "Sample Unbiased Variance"), name = "Estimator") +
scale_x_continuous(breaks = seq(10, 200, 10)) +
theme_classic() +
theme(text = element_text(size = 25)) 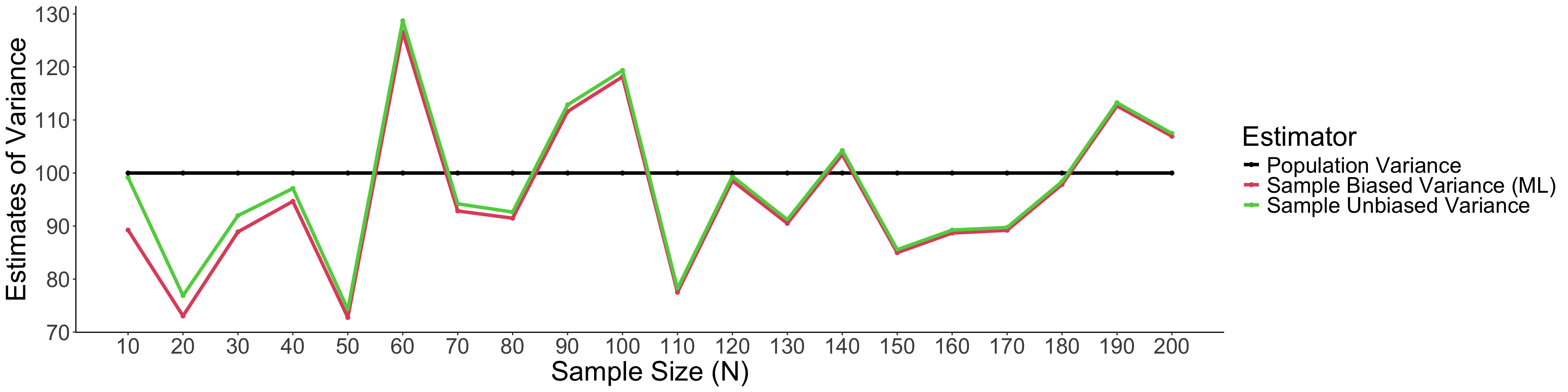
Take home note: When sample size is small, unbiased variance estimators can get the estimate of variance closer to the population variance than the biased one.
Interpretation of Variance
The variance (\(\sigma^2\) and \(S^2\)) describes the spread of a variable in squared units (which come from \((Y_p - \bar Y)^2\) term in the equation)
Variance: the average squared distance of an observation from the mean
For the toy sample, the variance of height is 55.358 inches squared
For the toy sample, the variance of weight is 3179.095 pounds squared
The variance of female — not applicable in the same way!
- How is the sample equally distributed across different groups: 50/50 -> largest variance
Because squared units are difficult to work with, we typically use the standard deviation – which is reported in units
Standard deviation: the average distance of an observation from the mean
SD of Height: 7.44 inches
SD of Weight: 56.383 pounds
Variance/SD as a More General Statistical Concept
- Variance (and the standard deviation) is a concept that is applied across statistics – not just for data
- Statistical parameters (slope, intercept) have variance
- e.g., The sample mean \(\bar Y\) has a “standard error” (SE) of \(S_{\bar Y} = S_Y / \sqrt{N}\)
- How accurately we can estimate the sample mean \(\neq\) How dispersed the samples are
- Statistical parameters (slope, intercept) have variance
- The standard error is another name for standard deviation
- So “standard error of the mean” is equivalent to “standard deviation of the mean”
- Usually “error” refers to parameters; “deviation” refers to data
- Variance of the mean would be \(S_{\bar Y}^2 = S^2_Y / N\)
Example: Table of Descriptive Statistics
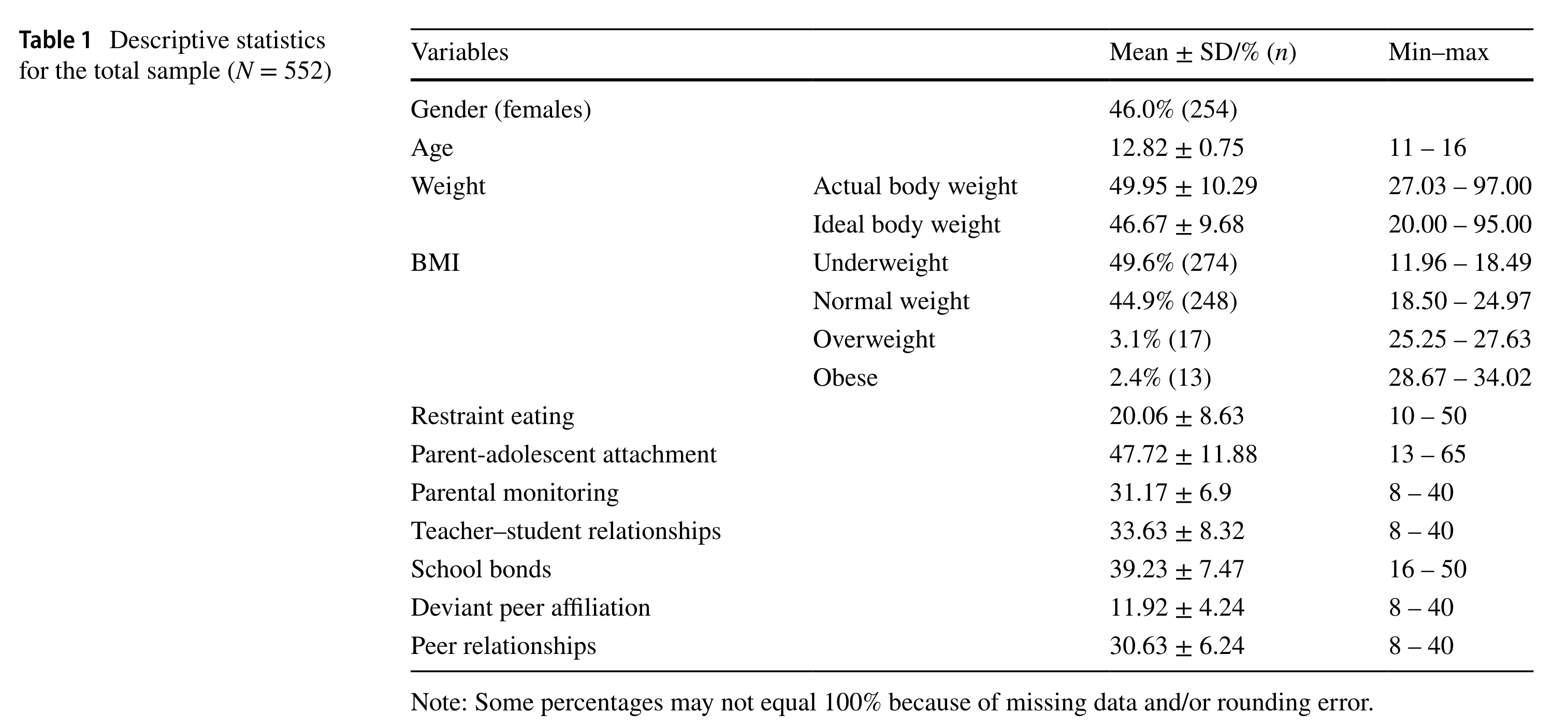
Table 1 (Xiong et al., 2023)
Key information that be reprted
All variables that you think relevant to the study: (1) demographic (2) context factors (3) outcomes or predictors
Categorical Variables: (1) Percentage of each level (2) Sample size of each level (3) Range
Continuous Variables: Mean + SD + Range
Correlation of Variables
- Moving from marginal summaries of each variable to joint (bivariate) summaries, we can use the Pearson Correlation to describe the association between a pair of continuous variables:
\[ r_{Y_1, Y_2} = \frac{\frac{1}{N-1}\sum_{p=1}^N (Y_{1p}-\bar Y_1) (Y_{2p}-\bar Y_2)}{S_{Y_1}S_{Y_2}} \\ = \frac{\sum_{p=1}^N (Y_{1p}-\bar Y_1) (Y_{2p}-\bar Y_2)}{\sqrt{\sum_{p=1}^{N} (Y_{1p}-\bar Y)^2}\sqrt{\sum_{p=1}^{N} (Y_{2p}-\bar Y)^2}} \]
Human words: how much Variable 1 vary with Variable 2 relative to their own variability.
Note that pearson correlation does not take other variables into account
R: Pearson Correlation
Method 1: Use R function
cor() function with the argument method = “pearson”
[1] -1
[1] 1
X Y Z
X 1 -1 1
Y -1 1 -1
Z 1 -1 1Method 2: Manual way
sum() adds up all numbers of vector within the parenthesis
X-mean(X) returns the mean centered values of X
Two vectors can be multiplied with each other and return a new vector: X*Y
length() return the number of values of X
More on the Correlation Coefficient
The Pearson correlation is a biased estimator
- Biased estimator: the expected value differs from the true value for a statistic
The unbiased version of correlation estimation would be:
\[ r_{Y_1, Y_2}^U= r_{Y_1,Y_2}(1+\frac{1-r^2_{Y_1,Y_2}}{2N}) \]
Properties of biased estimator:
As N gets large bias goes away;
Bias is largest when \(r_{Y_1, Y_2} =0\); Pearson Corr. is unbiased when \(r_{Y_1, Y_2} =1\)
Pearson correlation is an underestimate of true correlation
Covariance: Association with Units
The numerator of the Pearson correlation (\(r_{Y_1Y_2}\)) is the Covariance
- Human words: “Unscaled (Unstandardized)” Correlation
\[ S^2_{Y_1, Y_2}= \frac{\sum_{p=1}^{N}(Y_{1p}-\bar Y_1)(Y_{2p}-\bar Y_2)}{N-1} \]
\[ S^2_{Y_1, Y_2}= \frac{\sum_{p=1}^{N}(Y_{1p}-\bar Y_1)(Y_{2p}-\bar Y_2)}{N}\]
Variance is a special Covariance so that the variable covary with itself
The covariance uses the units of the original variables (but now they are multiples):
- Covariance of height and weight: 334.832 inch-pounds
The covariance of a variable with itself is the variance
The covariance if often used in multivariate analyses because it ties directly into multivariate distribution
- Covariance and correlation are easy to switch between
Going from Covariance to Correlation
If you have the covariance matrix (variances and covariances):
\[ r_{Y_1,Y_2}=\frac{S_{Y_1,Y_2}}{S_{Y_1}S_{Y_2}} \]
If you have the correlation matrix and the standard deviations:
\[ S_{Y_1, Y_2} = r_{Y_1, Y_2} S_{Y_1} S_{Y_2} \]
Summary of Unit 1
- Descriptive statistics: describe central tendency and variability of variables in a visual or statistical way.
- Visual way: Histogram, Scatter plot, Density plot
- Statistical way: mean/mode/median; variance/standard deviation
- Alternatively, we cab describe the relationships between two or more variables using their joint distributions
- Visual way: Scatter plot, Group-level Histogram
- Statistical way: Covariance, Pearson Correlation, Chi-square (\(\chi^2\)) test
Unit 2: General Linear Model
Learning Objectives
Types of distributions:
- Conditional distribution: a special joint distribution condition on other variable
The General Linear Model
Regression
Analysis of Variance (ANOVA)
Analysis of Covariance (ANCOVA)
Beyond – Interactions
Taxonomy of GLM
- The general linear model (GLM) incorporates many different labels of analysis under one unifying umbrella:
| Categorical Xs | Continuous Xs | Both Types of Xs | |
|---|---|---|---|
| Univariate Y | ANOVA | Regression | ANCOVA |
| Multivariate Ys | MANOVA | Multivariate Regression | MANCOVA |
The typical assumption is that error term (residual or \(\epsilon\)) is normally distribution – meaning that the data are conditionally normally distributed
Models for non-normal outcomes (e.g., dichotomous, categorical, count) fall under the Generalized Linear Model, of which general linear model is a special case
Property of GLM: Conditional Normality of Outcome
The general form of GLM with two predictors:
\[ Y_p = {\color{blue}\beta_0+\beta_1X_p+\beta_2Z_p+\beta_3X_pZ_p} + {\color{red}e_p} \]
Model for the Means (Predicted Values):
Each person’s expected (predicted) outcome is a function of his/her values x and z (and their interaction)
y, x, and z are each measured only once per person (p subscript)
Model for the Variance:
\(e_p \sim N(0, \sigma_e^2)\) \(\rightarrow\) One residual (unexplained) deviation
\(e_p\) has a mean of 0 and variance of \(\sigma^2_e\) and is normally distributed, unrelated to x and z, unrelated across observation
Model for the variance is important for model evaluation
Example: Building a GLM for Weight Prediction
Goal: build a GLM for predicting a person’s weight, using height and gender as predictors
Plan: we proposed several models for didactic reasons — to show how regression and ANOVA work with GLM
- In practice, you wouldn’t necessarily run these models in this sequence
Beginning model (Model 1): An empty model – no predictors for weight (an unconditional model)
Final model (Model 5): A full model – include all predictors and their interaction model
Example: All models
- Model 1
\[ \hat{ \text{Weight}_p }= \beta_0 \]
- Model 2:
\[ \hat{\text{Weight}_p} =\beta_0 + \beta_1\text{Height}_p \]
- Model 2a:
\[ \hat{\text{Weight}_p} =\beta_0 + \beta_1\text{HeightC}_p \]
- Model 3:
\[ \hat{\text{Weight}_p}=\beta_0+\beta_2\text{Female}_p \]
- Model 4:
\[\hat{\text{Weight}_p}=\beta_0+\beta_1\text{HeightC}_p+\beta_2\text{Female}_p\]
- Model 5:
\[\hat{\text{Weight}_p}=\beta_0+\beta_1\text{HeightC}_p+\beta_2\text{Female}_p \\ + \beta_3\text{HeigthCxFemale}_p\]
Model 1: Empty Model
\[ \text{Weight}_p = \beta_0 + e_p \] \[ e_p \sim N(0, \sigma^2_e) \]
Estimated parameters:
\(\beta_0\): Overall intercept - the “grand” mean of weight across all people
\(e_p\): Residual error - how each one’s observes deviate from \(\beta_0\)
\(\sigma^2_e\): Residual variance - variability of residual error across all people
R Code
library(ESRM64503)
library(kableExtra)
model1 <- lm(weightLB ~ 1, data = dataSexHeightWeight) # model formula
summary(model1)$coefficients |> kable() # regression cofficients table| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 183.4 | 12.60773 | 14.54664 | 0 |
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| Residuals | 19 | 60402.8 | 3179.095 | NA | NA |
Interpretation
- \(\beta_0 = 183.4\) is the predicted value of a Weight for all people is 183.4 pound
- Just the mean of weight
- \(SE(\beta_0) = 12.60\) is the standard error of the mean for weight with higher value suggesting more inaccuracy
- \(t = 14.55, p < .001\) is t-test of the parameter suggesting the mean of weight significantly deviate from 0
- Error term / Residual: \(\sigma^2_e = 3179.095\) (variance of the residuals)
- Equal to the unbiased variance of weight in empty model
- Also know as Mean Square Error in F-table
- \(\beta_0 = 183.4\) is the predicted value of a Weight for all people is 183.4 pound
Model 2: Predicting Weight from Height
\[ \text{Weight}_p = \beta_0 + \beta_1 \text{Height}_p + e_p \] \[ e_p \sim N(0, \sigma^2_e) \]
Estimated parameters:
\(\beta_0\): Intercept - is the predicted value of a Weight for a people with Height is 0
\(\beta_1\): Slope of Height - the predicted increase of Weight for one-unit increase in Height
\(e_p\): Residual error - how each one’s observes deviate from \(\beta_0\)
\(\sigma^2_e\): Residual variance - variability of residual error across all people
R code
model2 <- lm(weightLB ~ heightIN, data = dataSexHeightWeight) # model formula
summary(model2)$coefficients |> kable(digit = 3) # regression cofficients table| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | -227.292 | 73.483 | -3.093 | 0.006 |
| heightIN | 6.048 | 1.076 | 5.621 | 0.000 |
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| heightIN | 1 | 38479.27 | 38479.273 | 31.593 | 0 |
| Residuals | 18 | 21923.53 | 1217.974 | NA | NA |
Interpretation
- \(\beta_0 = -227.3\) is the predicted value of a Weight for a people with Height is 0
- Nonsensical – but we can fix it by centering Height
- \(\beta_1 = 6.048\): Weight goes up 6.048 per inch
- \(SE(\beta_1) = 1.076\): the inaccuracy of \(\beta_1\); \(CI = 6.048 \pm 1.96\times 1.076\)
- \(t = 5.621, p < .001\) is t-test of the parameter suggesting the slope of height significantly deviate from 0
- \(F(1, 18) = 31.593 = \frac{38479.273}{1217.974} = t^2\)
- Error term / Residual: \(\sigma^2_e = 1217.974\) (variance of the residuals)
- Height explains \(\frac{3179.095-1217.974}{3179.095}=61.7\%\) of variance of weight
- \(\beta_0 = -227.3\) is the predicted value of a Weight for a people with Height is 0
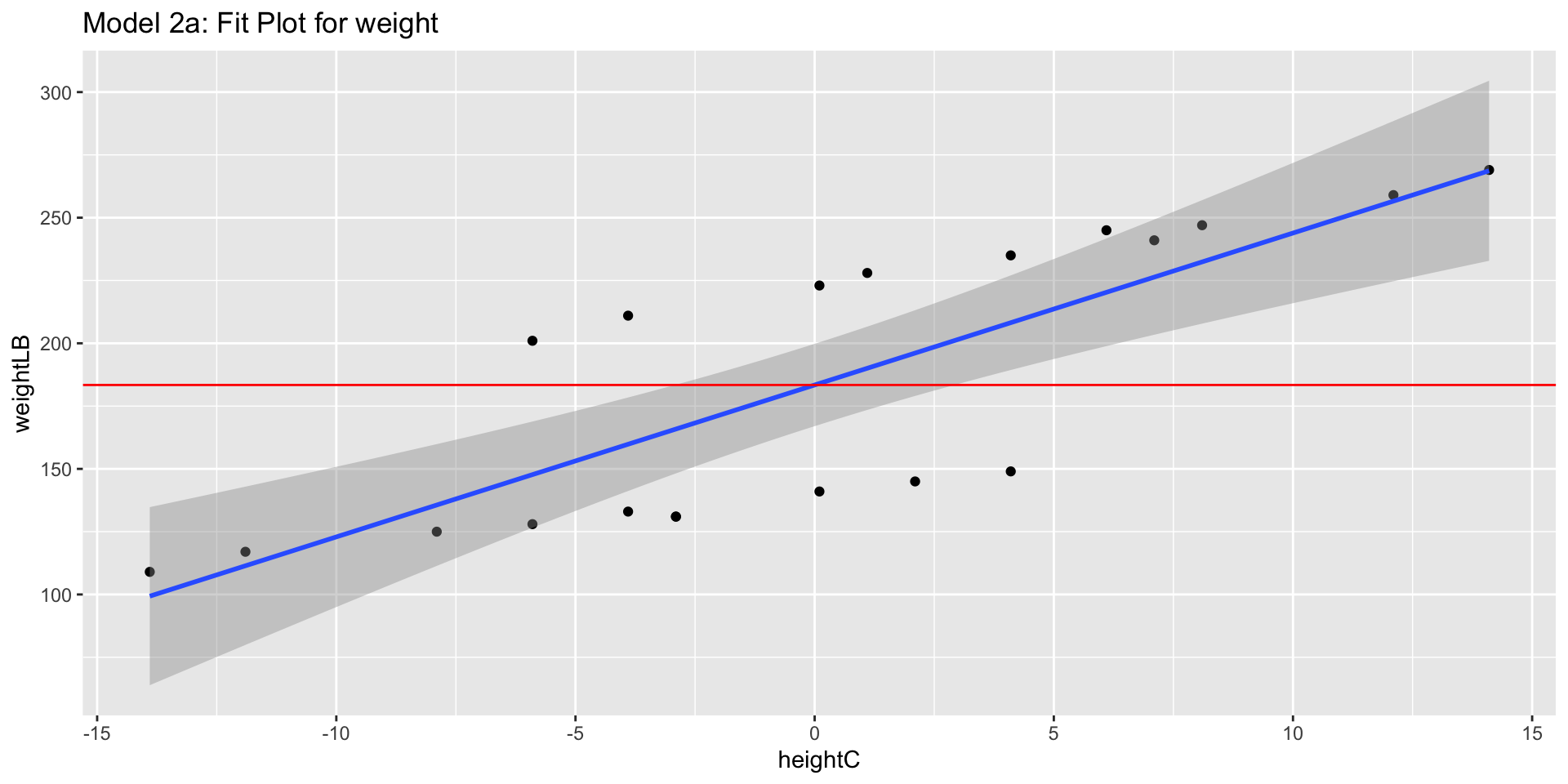
Model 2a: Predicting Weight from Centered Height
\[ \text{Weight}_p = \beta_0 + \beta_1 (\text{Height}_p - \bar{Height}) + e_p \\ = \beta_0 + \beta_1 \text{HeightC}_p + e_p \] \[ e_p \sim N(0, \sigma^2_e) \]
Estimated parameters:
\(\beta_0\): Intercept - is the predicted value of a Weight for a people with Height is Mean Height
\(\beta_1\): Slope of Height - the predicted increase of Weight for one-unit increase in Height
\(e_p\): Residual error - how each one’s observes deviate from \(\beta_0\)
\(\sigma^2_e\): Residual variance - variability of residual error across all people
R code
dataSexHeightWeight$heightC = dataSexHeightWeight$heightIN - mean(dataSexHeightWeight$heightIN)
model2a <- lm(weightLB ~ heightC, data = dataSexHeightWeight) # model formula
summary(model2a)$coefficients |> kable(digit = 3) # regression cofficients table| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 183.400 | 7.804 | 23.501 | 0 |
| heightC | 6.048 | 1.076 | 5.621 | 0 |
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| heightC | 1 | 38479.27 | 38479.273 | 31.593 | 0 |
| Residuals | 18 | 21923.53 | 1217.974 | NA | NA |
Interpretation
- \(\beta_0 = 183.4\) pounds (previously -227.3) is the predicted value of a Weight for a people with Height is 67.9 inches
- Everything except \(\beta_0\), \(SE(\beta_0)\), and t-value of intercept should be same as the previous model
Visualization
Wrap up: Hypothesis Tests for Parameters
- To determine if the regression slope is significantly different from zero, we must use a hypothesis test:
\[ H_0: \beta_1 = 0 \]
\[ H_1: \beta_1 \neq 0 \]
We have two options for this test (both are same here)
Use ANOVA table: sums of squares – F-test
Use “Wald” test for parameter: \(t = \frac{\beta_1}{SE(\beta_1)}\)
Here \(t^2 = F\)
p < 0.001 \(\rightarrow\) reject null (\(H_0\)) \(\rightarrow\) Conclusion: slope is significant
Model 3: Predicting Weight from Gender
\[ \text{Weight}_p = \beta_0 + \beta_1 \text{Female}_p + e_p \] \[ e_p \sim N(0, \sigma^2_e) \]
Note: because gender is a categorical predictor, we must first code it into a number before entering it into model (typically done automatically in software)
- Here we code the variable as Female = 1 for females; Female = 0 for males
Estimated parameters:
\(\beta_0\): Intercept - predicted value of Weight for a person with Female = 0 (males)
\(\beta_2\): Slope of Female - Change in predicted value of Weight between Males and Famales
R Code
model3 <- lm(weightLB ~ female, data = dataSexHeightWeight) # model formula
summary(model3)$coefficients |> kable(digit = 3) # regression cofficients table| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 235.9 | 5.415 | 43.565 | 0 |
| femaleTRUE | -105.0 | 7.658 | -13.711 | 0 |
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| female | 1 | 55125.0 | 55125.000 | 188.004 | 0 |
| Residuals | 18 | 5277.8 | 293.211 | NA | NA |
Interpretation
- \(\beta_0 = 235.9\) pounds is the predicted value of a Weight for a male
- \(\beta_0 +\beta_1 = 235.9 - 105.0 = 130.9\) pounds is the predicted value of a Weight for a female
- \(\beta_1 = 105\) expected difference between gender, which is significant based on t-test and F-test
Visualization:
Line Plot (not frequently used in this case)
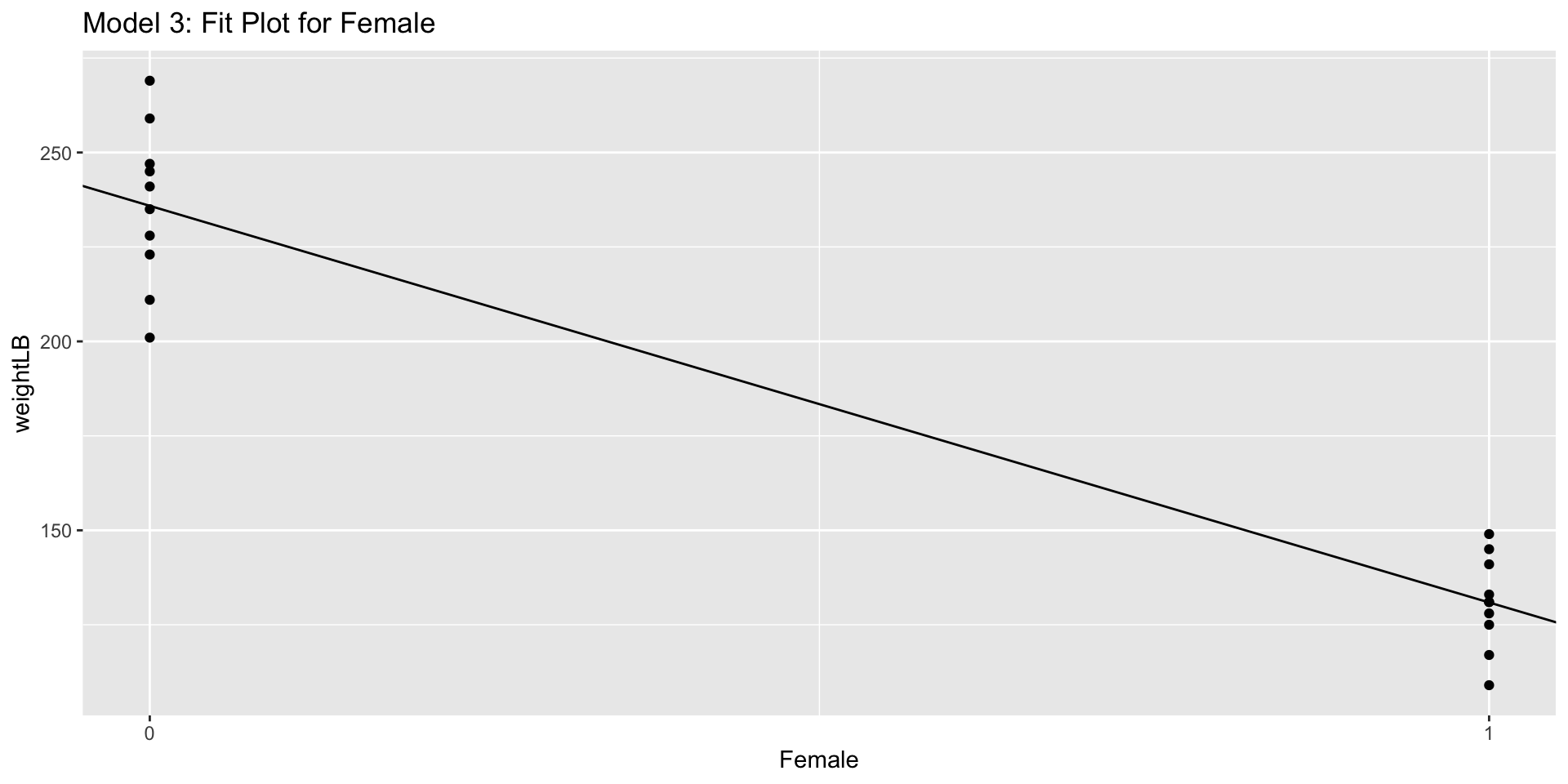
Visualization: box-and-whisker plot (Basic Way)
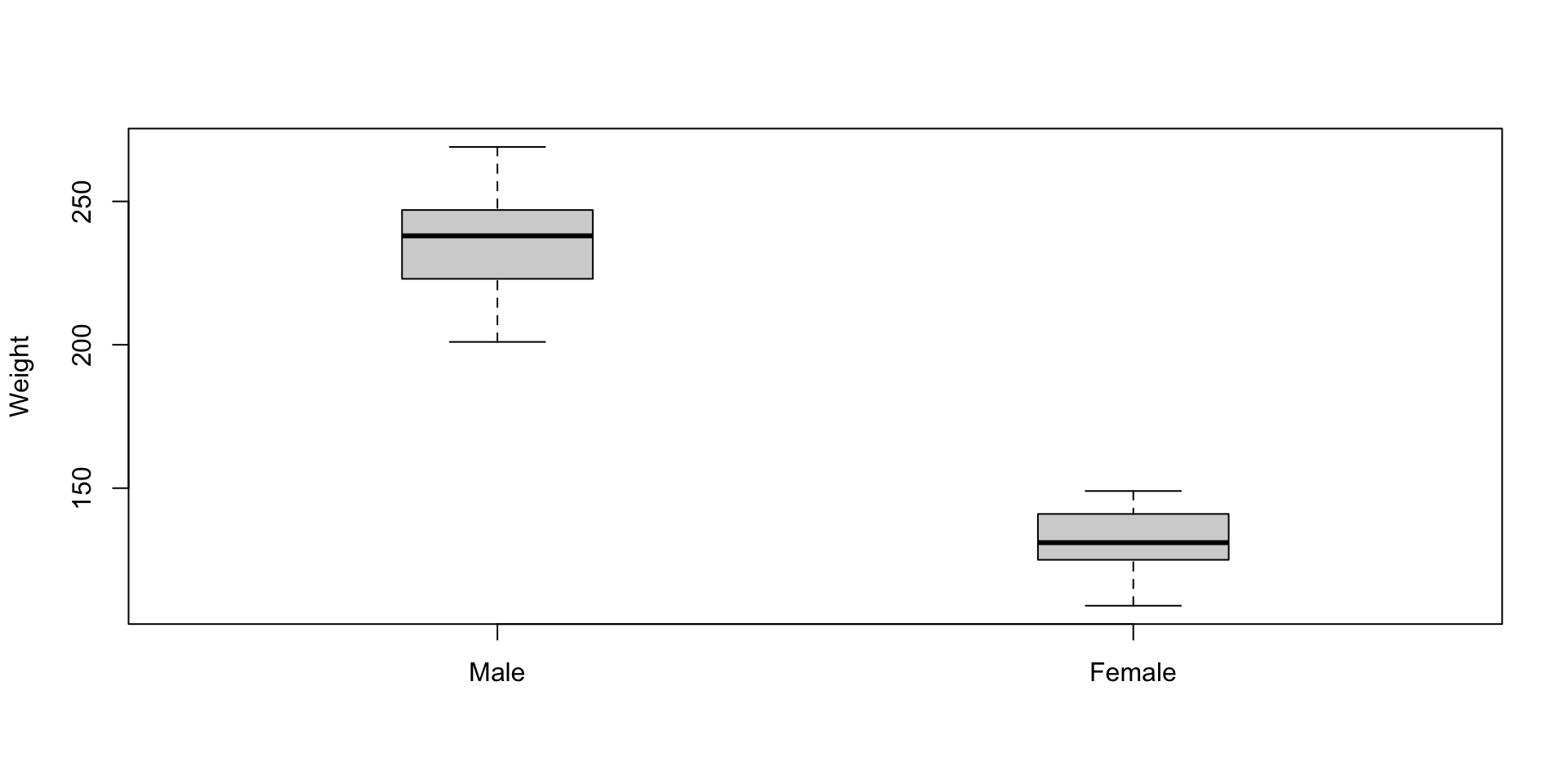
Visualization: box-and-whisker plot (Fancy Way)
ggplot2 package
ggplot(dataSexHeightWeight, aes(x = female, y = weightLB)) +
geom_dotplot(aes(fill = female, color = female), binaxis='y', stackdir='center') +
stat_summary(fun.data= "mean_cl_normal", fun.args = list(conf.int=.75), geom="crossbar", width=0.3, fill = "yellow", alpha = .5) +
stat_summary(fun.data= "median_hilow", geom="errorbar", fun.args = list(conf.int=1), width = .1, color="black") + # Mean +- 2SD
stat_summary(fun.data= "mean_sdl", geom="point", shape = 5, size = 3) +
scale_x_discrete(labels = c("Male", "Female")) +
labs(x = "", y = "Weight") +
theme_bw() +
theme(legend.position = "none", text = element_text(size = 20)) 
Model 4: Predicting Weight from Height and Gender
\[ \text{Weight}_p = \beta_0 + \beta_1 \text{HeightC}_p + \beta_2 \text{Female}_p + e_p \] \[ e_p \sim N(0, \sigma^2_e) \]
model4 <- lm(weightLB ~ heightC + female, data = dataSexHeightWeight) # model formula
summary(model4)$coefficients |> kable(digit = 3) # regression cofficients table| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 224.256 | 1.439 | 155.876 | 0 |
| heightC | 2.708 | 0.155 | 17.525 | 0 |
| femaleTRUE | -81.712 | 2.241 | -36.461 | 0 |
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| heightC | 1 | 38479.273 | 38479.273 | 2363.103 | 0 |
| female | 1 | 21646.710 | 21646.710 | 1329.376 | 0 |
| Residuals | 17 | 276.817 | 16.283 | NA | NA |
Interpretation
\(\beta_0 = 224.256 (SE = 1.439)\)
- The predicted weight is 224.256 pounds for a person with Female = 0 (males) and has Height as Mean Height 67.9 inches
\(\beta_1 = 2.708 (SE = 0.155)\)
\(t = \frac{2.708}{0.155}=17.525; p <.001\)
The expected change in weights for every one-unit increase in height holding gender constant
\(\beta_2=-81.713 (SE = 2.241)\)
- The expected difference between the mean of weights for males and the mean for females holding height constant
\(\sigma_e^2 = 16.283\)
- The residual variance of weight
Model 4: By-Gender Regression Lines
Model 4 assumes identical regression slopes for both genders but has different intercepts
- This assumption of different slopes will be tested statistically by model 5
Predicted Weight for Females with the height as 68.9 inch:
\[ W_p=224.256+2.708\times\color{blue}{(68.9-67.9)} - 81.713*\color{red}{1} \\ = 224.256+2.708-81.712 = 145.252 \]
Predicted Weight for Males with the height as 68.9 inch:
\[ W_p=224.256+2.708\times\color{blue}{(68.9-67.9)} - 81.713*\color{red}{0} \\ = 224.256+2.708 = 226.964 \]
1
145.252
1
226.9639 Visualization: Different intercept and Same slope across groups
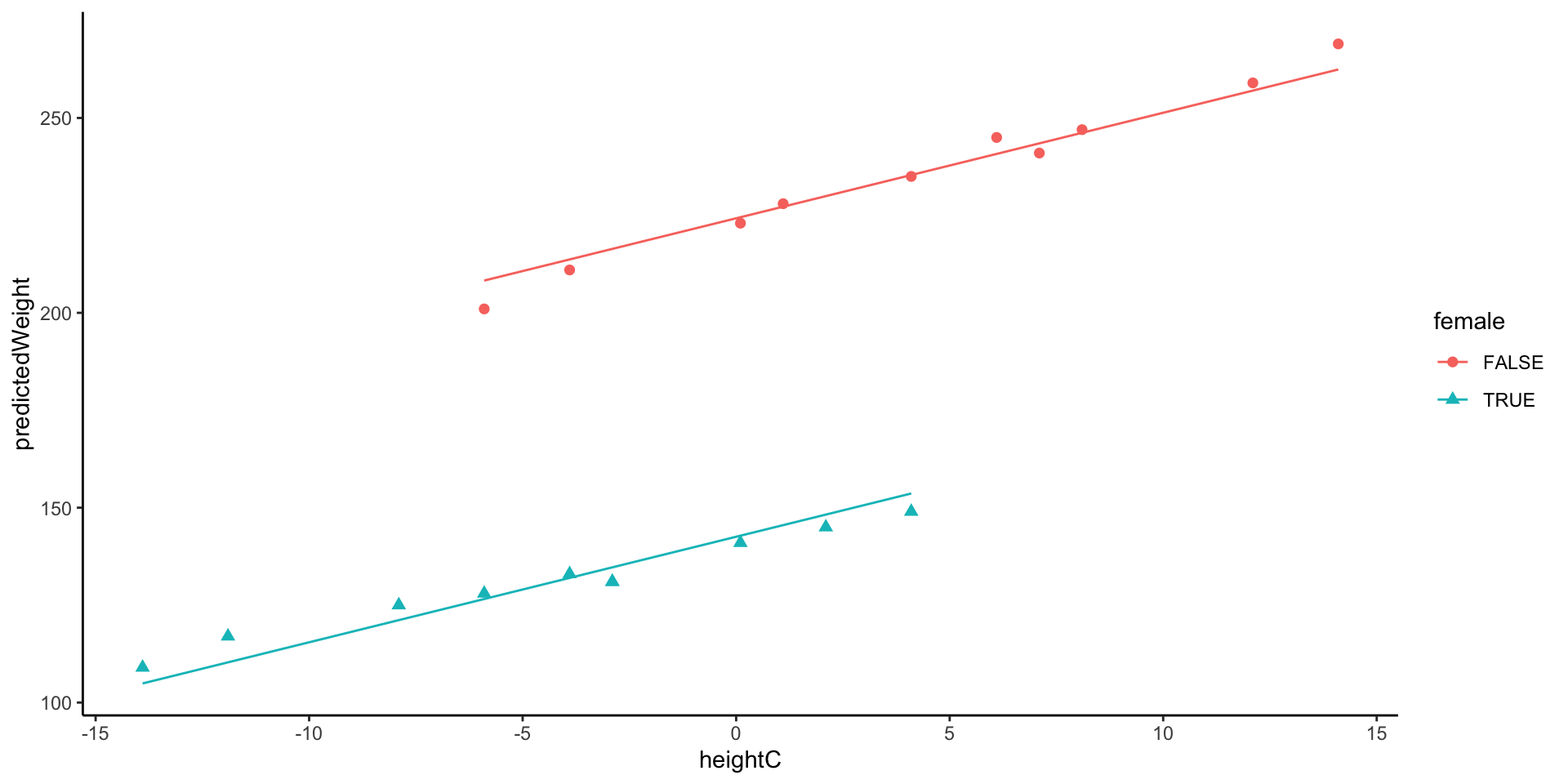
Model 5: By-Gender Regression Lines
\[\text{Weight}_p = \beta_0 + \beta_1 \text{HeightC}_p + \beta_2 \text{Female}_p +\beta_3 \text{HeightCxFemale}_p+ e_p\]
model5 <- lm(weightLB ~ heightC * female, data = dataSexHeightWeight) # model formula
summary(model5)$coefficients |> kable(digit = 3) # regression cofficients table| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 222.184 | 0.838 | 265.107 | 0 |
| heightC | 3.190 | 0.111 | 28.646 | 0 |
| femaleTRUE | -82.272 | 1.211 | -67.932 | 0 |
| heightC:femaleTRUE | -1.094 | 0.168 | -6.520 | 0 |
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| heightC | 1 | 38479.273 | 38479.273 | 8132.723 | 0 |
| female | 1 | 21646.710 | 21646.710 | 4575.104 | 0 |
| heightC:female | 1 | 201.115 | 201.115 | 42.506 | 0 |
| Residuals | 16 | 75.703 | 4.731 | NA | NA |
Interpretation
\(\beta_0 = 222.184 (SE = 0.838)\)
SE gets smaller compared to Model 4.
The predicted weight is 224.184 pounds for a person with Female = 0 (males) and has Height as Mean Height 67.9 inches
\(\beta_1 = 3.189 (SE = 0.111)\)
SE gets smaller compared to Model 4.
Simple main effect of Height: the expected change in weights for every one-unit increase in height for males only
\(\beta_2=-82.271 (SE = 1.211)\)
SE gets smaller compared to Model 4.
Simple main effect of gender: The expected difference between the mean of weights for males and the mean for females for people with mean height
\(\beta_3 = -1.093 (SE = 1.211)\) , \(t = -6.52, p < .001\)
Gender-by-Height Interaction: Additional change in slope of height for change in gender.
The slope of heights for males is 3.189; the slope of heights decreases 1.093 (2.096) inches/pound for females
\(\sigma_e^2 = 5\)
- Compared to 16.283 in model 4
Visualization: Different slopes and different intercepts
Model 5 does not assume identical regression slopes
- Because \(\beta_3\) was significantly different from zero, the data supports different slopes for the gender
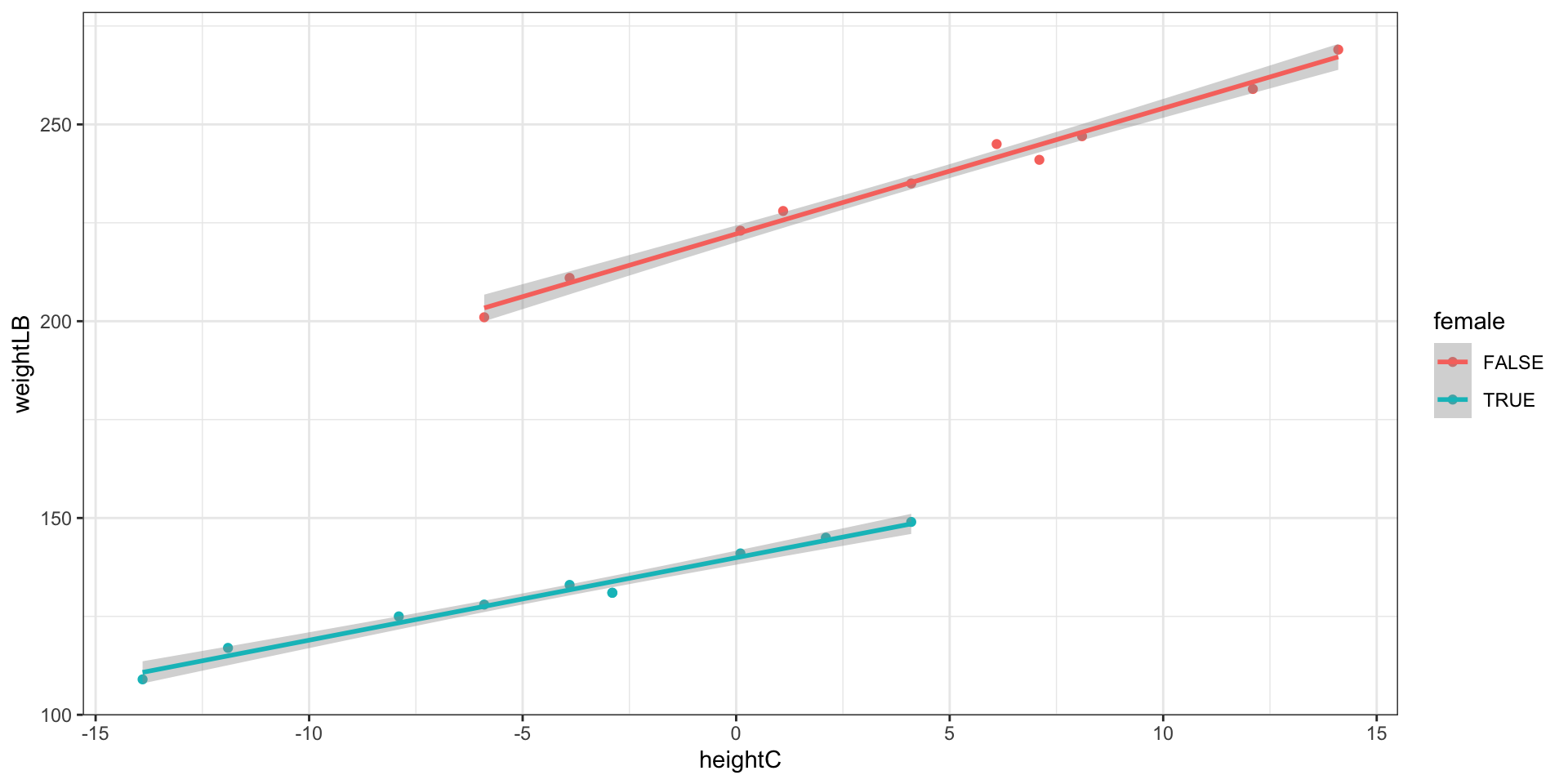
Model Comparison
In practice, the empty model (Model 0) and the full model (Model 5) would be the only models to run
The aim of model comparison is to decide on whether we want more complex model or the simple one
The trick is to describe the impact of all and each of the predictors – typically using variance accounted for
Residual Variance and \(R^2\)
Code
get_res_var <- function(model) {
anova(model)$`Mean Sq` |> tail(1)
}
data.frame(
Model = paste("Model", c(1, 2, "2a", 3, 4, 5)),
ResidualVariance = sapply(list(model1, model2, model2a, model3, model4, model5), get_res_var)
) |>
ggplot(aes(x = Model, y = ResidualVariance)) +
geom_point() +
geom_path(group = 1) +
geom_label(aes(label = round(ResidualVariance, 2)),nudge_y = 200, nudge_x = 0.2) +
labs(title = "Estimated Residual Variances across models") +
theme(text = element_text(size = 20))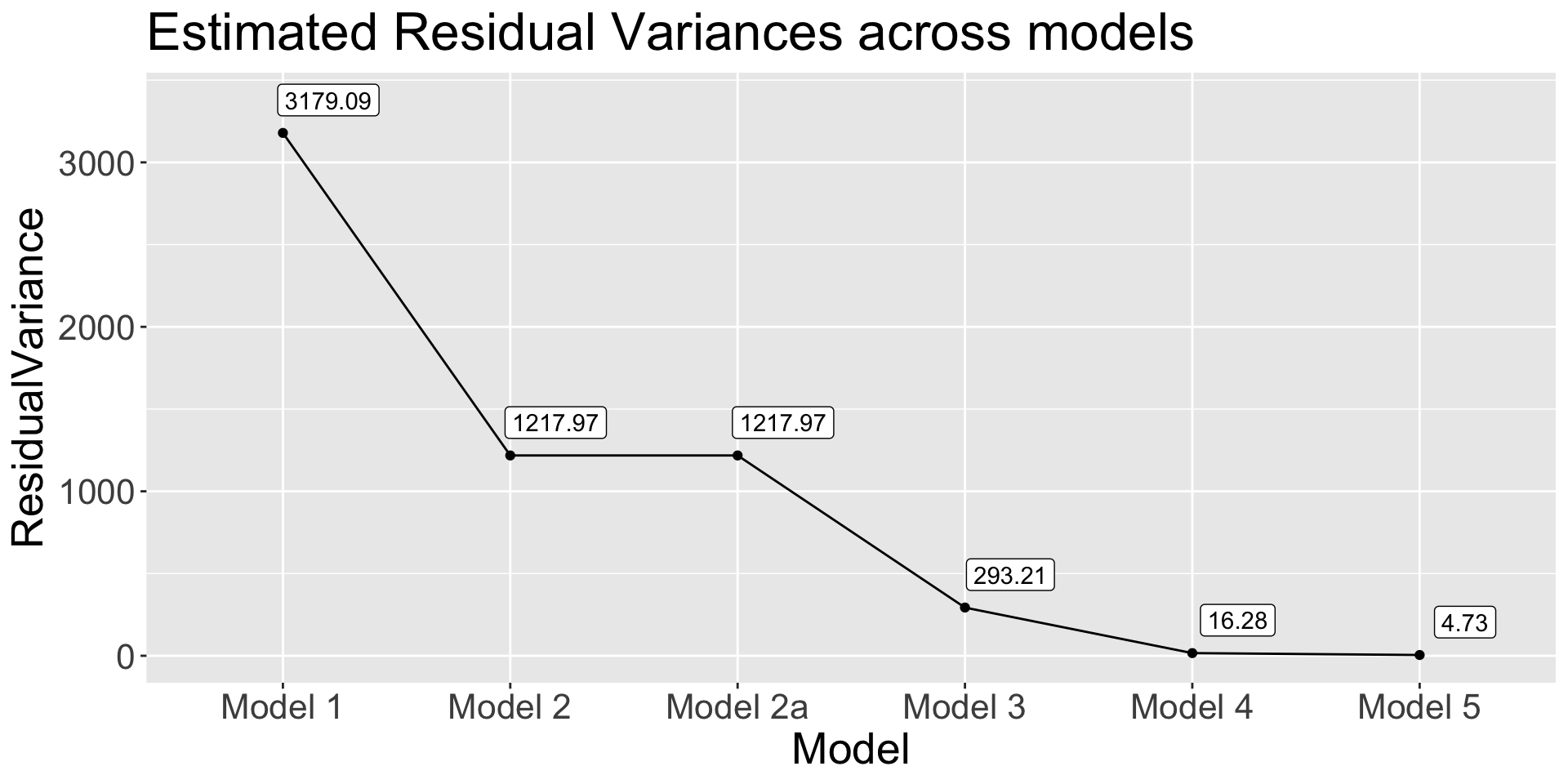
Code
get_explained_var <- function(model) {
tot_err_var <- anova(model1)$`Mean Sq` |> tail(1)
current_err_var <- anova(model)$`Mean Sq` |> tail(1)
prop <- (tot_err_var - current_err_var)/ tot_err_var
prop
}
data.frame(
Model = paste("Model", c(1, 2, "2a", 3, 4, 5)),
ExplainedVariance = sapply(list(model1, model2, model2a, model3, model4, model5), get_explained_var)
) |>
ggplot(aes(x = Model, y = ExplainedVariance)) +
geom_point() +
geom_path(group = 1) +
geom_label(aes(label = paste0(round(ExplainedVariance*100, 2), "%")),nudge_y = .05) +
labs(title = "Proportions of Explained Variance across Models")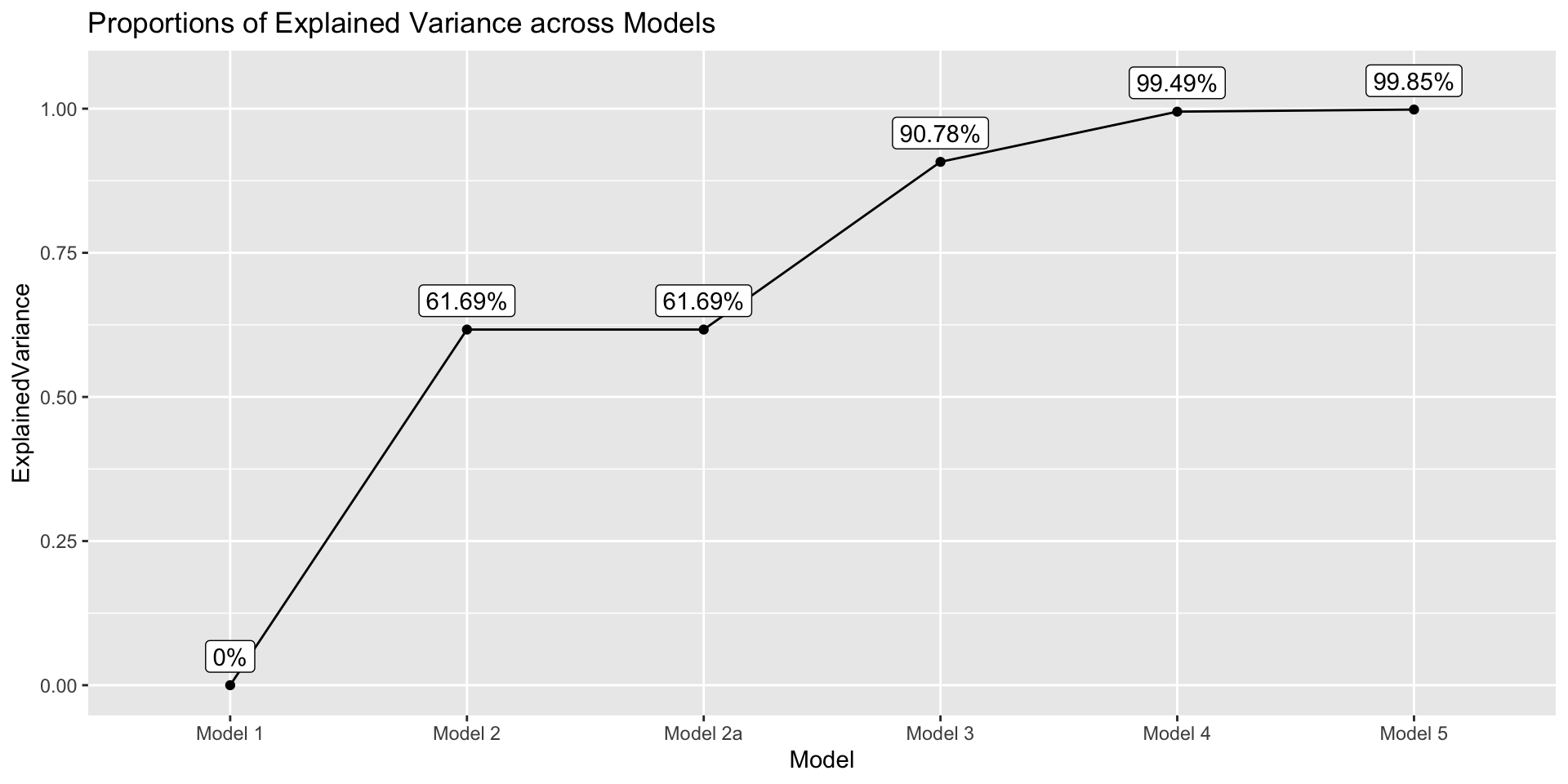
Comparison Across Models
- Are height and gender are good predictors?
- Total explained variances in weight by height and gender: Multiple \(R^2\) of Model 5
- \((3179.09-4.73)/3179.09 = 0.9985\) \(\rightarrow\) 99.85% variances in weights can be explained by height and gender
- F-test comparing Model 5 to Model 1
\(F_{3, 16} = 4250.1\), p < .001
Call: lm(formula = weightLB ~ heightC * female, data = dataSexHeightWeight) Residuals: Min 1Q Median 3Q Max -3.8312 -1.7797 0.4958 1.3575 3.3585 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 222.1842 0.8381 265.11 < 2e-16 *** heightC 3.1897 0.1114 28.65 3.55e-15 *** femaleTRUE -82.2719 1.2111 -67.93 < 2e-16 *** heightC:femaleTRUE -1.0939 0.1678 -6.52 7.07e-06 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 2.175 on 16 degrees of freedom Multiple R-squared: 0.9987, Adjusted R-squared: 0.9985 F-statistic: 4250 on 3 and 16 DF, p-value: < 2.2e-16
- Total explained variances in weight by height and gender: Multiple \(R^2\) of Model 5
- Are Height alone a good predictor?
Explained remaining variances in weight by height: Multiple \(R^2\) of Model 5 to Model 3
- \((293.21-4.73)/293.21 = 0.9839\) \(\rightarrow\) 98.39% variances in weights remaining after gender can be explained by the main and interaction effects of height
F-test comparing Model 5 to Model 3
\(F_{2, 16} = 548.74\), p < .001 suggests the effect of hight on weight is significant after controlling the effect of gender
True explained variances out of total variances in weight: Unique contribution of adding Height into the model
Check model 3, we can found that gender explained 90.78% variance of weight
\(0.9839 * (1 - 0.9078) = 0.0907\) \(\rightarrow\) 9.07% more variances of weights can be explained by height after gender is already in the model
90.78% + 9.07% = 99.85% is the total variance explained by height and gender
- Are gender alone a good predictor?
Explained remaining variances in weight by gender: Multiple \(R^2\) of Model 5 to Model 2a
- \((1217.97-4.73)/1217.97 = 0.9961\) \(\rightarrow\) 99.61% variances in weights remaining after height can be explained by the main and interaction effects of gender
F-test comparing Model 5 to Model 2a
\(F_{2, 16} = 2308.8\), p < .001 suggests the effect of gender on weight is significant after controlling the effect of height
True explained variances out of total variances in weight: Unique contribution of adding Height into the model
Check model 3, we can found that gender explained 90.78% variance of weight
\(0.9839 * (1 - 0.9078) = 0.0907\) \(\rightarrow\) 9.07% more variances of weights can be explained by height after gender is already in the model
90.78% + 9.07% = 99.85% is the total variance explained by height and gender
Summary of Unit 2
- We learned GLM using the 2-factor model
- For specific effect, we examine the t-test of coefficient
- For the total contribution of a bunch of effects (main + interaction), we look at R-square and F-test
- We sometime need to report predicted regression lines, which can be done in R with ggplot2
Unit 3: Let’s Look at R code together

ESRM 64503: Lecture 02 - Descriptive Statistics