Lecture 12: Principal Components Analysis and Exploratory Factor Analysis

ESRM 64503 - PCA and EFA

Jihong Zhang*, Ph.D

Educational Statistics and Research Methods (ESRM) Program*

University of Arkansas

2024-10-09

Course Evaluation

You will get 2 extra credit points if you finish the course evaluation.

Course	Course Name	Survey Open	Survey Close
ESRM 64503 - 001	APPLIED MULTIVARIATE STATS	Nov 21	Dec 6

Today’s Class

Methods for exploratory analysis
- Principal Components-based exploratory approach (PCA)
- Maximum Likelihood-based Exploratory Factor Analysis (EFA)
- Exploratory Structural Equation Modeling

library(ESRM64503)
library(kableExtra)
library(tidyverse)
library(DescTools) # Desc() allows you to quick screen data
library(lavaan) # Desc() allows you to quick screen data
# options(digits = 3)

The Logic of Exploratory Analysis

Exploratory analyses attempt to discover hidden structure in data with little to no user input
- Aside from the selection of analysis and estimation
The results from exploratory analyses can be misleading
- If data do not meet assumptions of model or method selected
- If data have quirks that are idiosyncratic to the sample selected
- If some cases are extreme relative to others
- If constraints made by analysis are implausible
Sometimes, exploratory analyses are needed
- Must construct an analysis that capitalizes on the known features of data
- There are better ways to conduct such analyses
Often, exploratory analyses are not needed
- But are conducted anyway – see a lot of reports of scale development that start with the idea that a construct has a certain number of dimensions

Advanced Matrix Operations

Matrix Orthogonality

A square matrix \(\Lambda\) is said to be orthogonal if:

\[ \mathbf{\Lambda\Lambda^T = \Lambda^T\Lambda = I} \]

For example, \(\mathbf \Lambda\) is a orthogonal matrix
- \[ \mathbf \Lambda = \frac{1}{7}\begin{bmatrix} 3 & 2 & 6 \\ -6 & 3 & 2 \\ 2 & 6 & 3 \end{bmatrix} \]
Orthogonal matrices are characterized by two properties
1. The dot product of all row vector multiples is the zero vector
  - Meaning vectors are orthogonal (or uncorrelated)
2. For each row vector, the sum of all elements is one
  - Meaning vectors are “normalized”
The matrix above is also called orthonormal
- The diagonal is equal to 1 (each vector has a unit length)
Orthonormal matrices are used in principal components and exploratory factor analysis

Eigenvalues and Eigenvectors

A square matrix \(\mathbf{\Sigma}\) can be decomposed into a set of eigenvalues \(\mathbf{\lambda}\) and a set of eigenvectors \(\mathbf e\):

\[ \mathbf{\Sigma e} = \lambda \mathbf{e} \]

Each eigenvalue has a corresponding eigenvector
- The number equal to the number of rows/columns of \(\mathbf{\Sigma}\)
Principal components analysis uses eigenvalues and eigenvectors to reconfigure data

R Code: Eigenvalues and Eigenvectors

In R, we can use eigen() function to get eigenvalues and eigenvectors of a square matrix (e.g., a correlation matrix).

library(ESRM64503)
## Correlation matrix of SAT-Verbal and SAT-Math
sat_corrmat = cor(dataSAT[, c("SATV", "SATM")])

## eignvalues and eigenvectors of correlation matrix:
sat_eigen = eigen(x = sat_corrmat, symmetric = TRUE)
sat_eigen$values # eigenvalues

[1] 1.7752238 0.2247762

sat_eigen$vectors # eigenvectors

          [,1]       [,2]
[1,] 0.7071068 -0.7071068
[2,] 0.7071068  0.7071068

In our SAT sample, the two eigenvalues obtained were:

\[ \lambda_1 = 1.775; \lambda_2 = 0.224 \\ \]

The two eigenvectors obtained were:

\[ \mathbf{e}_1 = \begin{bmatrix}0.707 \\ 0.707\end{bmatrix}; \mathbf{e}_2 = \begin{bmatrix}-0.707 \\ 0.707\end{bmatrix} \]

These terms will have much greater meaning principal components analysis

Spectral Decomposition

Using the eigenvalues and eigenvectors, we can reconstruct the original matrix using a spectral decomposition:

\[ \mathbf{\Sigma =}\sum_{i=1}^{p} \lambda_i\mathbf{e}_i \mathbf{e}_i^T \]

where \(i\) is the index of row/column of square matrix

For our example, we can get back to our 2*2 correlation matrix by combining two matrices of eigenvalues and eigenvectors:

\[ \mathbf{R}_1 = \lambda_1 \mathbf{e}_i \mathbf{e}_i^T = 1.775 \begin{bmatrix}0.707 \\ 0.707\end{bmatrix} \begin{bmatrix}0.707 & 0.707\end{bmatrix} = \begin{bmatrix}0.890 & 0.890\\ 0.890 & 0.890\end{bmatrix} \]

\[ \begin{align} \mathbf{R}_2 &= \mathbf{R}_1 +\lambda_1 \mathbf{e}_i \mathbf{e}_i^T \\ &= \begin{bmatrix}0.890 & 0.890\\ 0.890 & 0.890\end{bmatrix} + 0.224 \begin{bmatrix}-0.707 \\ 0.707\end{bmatrix} \begin{bmatrix}-0.707 & 0.707\end{bmatrix} \\ &= \begin{bmatrix}1.000 & 0.780\\ 0.780 & 1.000 \end{bmatrix} \end{align} \]

# spectral decomposition
1corr_rank1 = sat_eigen$values[1] * tcrossprod(sat_eigen$vectors[,1])
corr_rank1

1: tcrossprod: \(\mathbf{e}\mathbf{e}^T\)

          [,1]      [,2]
[1,] 0.8876119 0.8876119
[2,] 0.8876119 0.8876119

corr_rank2 = corr_rank1 + sat_eigen$values[2] * tcrossprod(sat_eigen$vectors[,2])
corr_rank2

          [,1]      [,2]
[1,] 1.0000000 0.7752238
[2,] 0.7752238 1.0000000

Additional Eigenvalue Properties

The matrix trace is the sum of the eigenvalues:

\[ tr(\mathbf\Sigma) = \sum_{i=1}^{p}\lambda_i \]

Note

The transformation of data: In Mathematics, an eigenvector corresponds to the real nonzero eigenvalues which point in the direction stretched by the transformation; eigenvalue is considered as a factor by which it is stretched.

In our example, the \(tr(\mathbf R) = 1.775 + 0.224 \approx 2\)

sum(sat_eigen$values)

[1] 2

The determinant of correlation matrix (the generalized variance) can be found by the product of the eigenvalues

\[ |\mathbf\Sigma| = \prod_{i=1}^p \lambda_i \]

In our example, the \(|\mathbf R| = 1.775 * 0.224 \approx .3976\)

PRINCIPAL COMPONENTS ANALYSIS (PCA)

PCA Overview

Principal Components Analysis (PCA) is a method for re-expressing the covariance (or often correlation) between a set of variables
- The re-expression comes from creating a set of new variables (linear combinations) of the original variables
PCA has two objectives:
1. Data reduction - Moving from many original variables down to a few “components”
  - You have 100 variables, but you only need 7 composite scores that summarizes all 100 variables.
2. Interpretation - Determining which original variables contribute most to the new “components”

Goals of PCA

The goal of PCA is to find a set of k principal components (composite variables) that:
- Is much smaller in number than the original set of V variables
- Accounts for nearly all of the total variance
  - Total variance = trace of covariance/correlation matrix
If these two goals can be accomplished, then the set of k principal components contains almost as much information as the original V variables
- Meaning – the components can now replace the original variables in any subsequent analyses

Questions when using PCA

PCA analyses proceed by seeking the answers to two questions:
1. How many components are needed to “adequately” represent the original data?
  - e.g., for 10-item depression survey, we may need one composite score of “deperssion”
  - The term “adequately” is fuzzy (and will be in the analysis)
2. (once #1 has been answered): What does each component represent?
  - The term “represent” is also fuzzy
  - e.g., what does the “component” score mean? For one component, it can be interpreted as “general depression level”. What about two or three components?

PCA Features

PCA often reveals relationships between variables that were not previously suspected
- New interpretations of data and variables often stem from PCA
PCA usually serves as more of a means to an end rather than an end it itself
- Components (the new variables) are often used in other statistical techniques
  - Multiple regression/ANOVA
  - Cluster analysis
Unfortunately, PCA is often intermixed with Exploratory Factor Analysis
- Don’t. Please don’t. Please make it stop.

PCA Formulas

Notation: \(Z\) are our new components and \(\mathbf Y\) is our original data matrix (with N observations and V variables)
- We will let p be our index for a subject
The new components are linear combinations:
- We can generate V number of components at most, same as number of observed variables:

\[ \begin{array}{c} Z_{p 1}=\mathbf{e}_{1}^{T} \mathbf{Y}=e_{11} Y_{p 1}+e_{21} Y_{p 2}+\cdots+e_{V 1} Y_{p V} \\ Z_{p 2}=\mathbf{e}_{2}^{T} \mathbf{Y}=e_{12} Y_{p 1}+e_{22} Y_{p 2}+\cdots+e_{V 2} Y_{p V} \\ \vdots \\ Z_{p V}=\mathbf{e}_{V}^{T} \mathbf{Y}=e_{1 V} Y_{p 1}+e_{2 V} Y_{p 2}+\cdots+e_{V V} Y_{p V} \end{array} \]

The weights of the components (\(e_{jk}\)) come from the eigenvectors of the covariance or correlation matrix for component k and variable j

Diagram of PCA

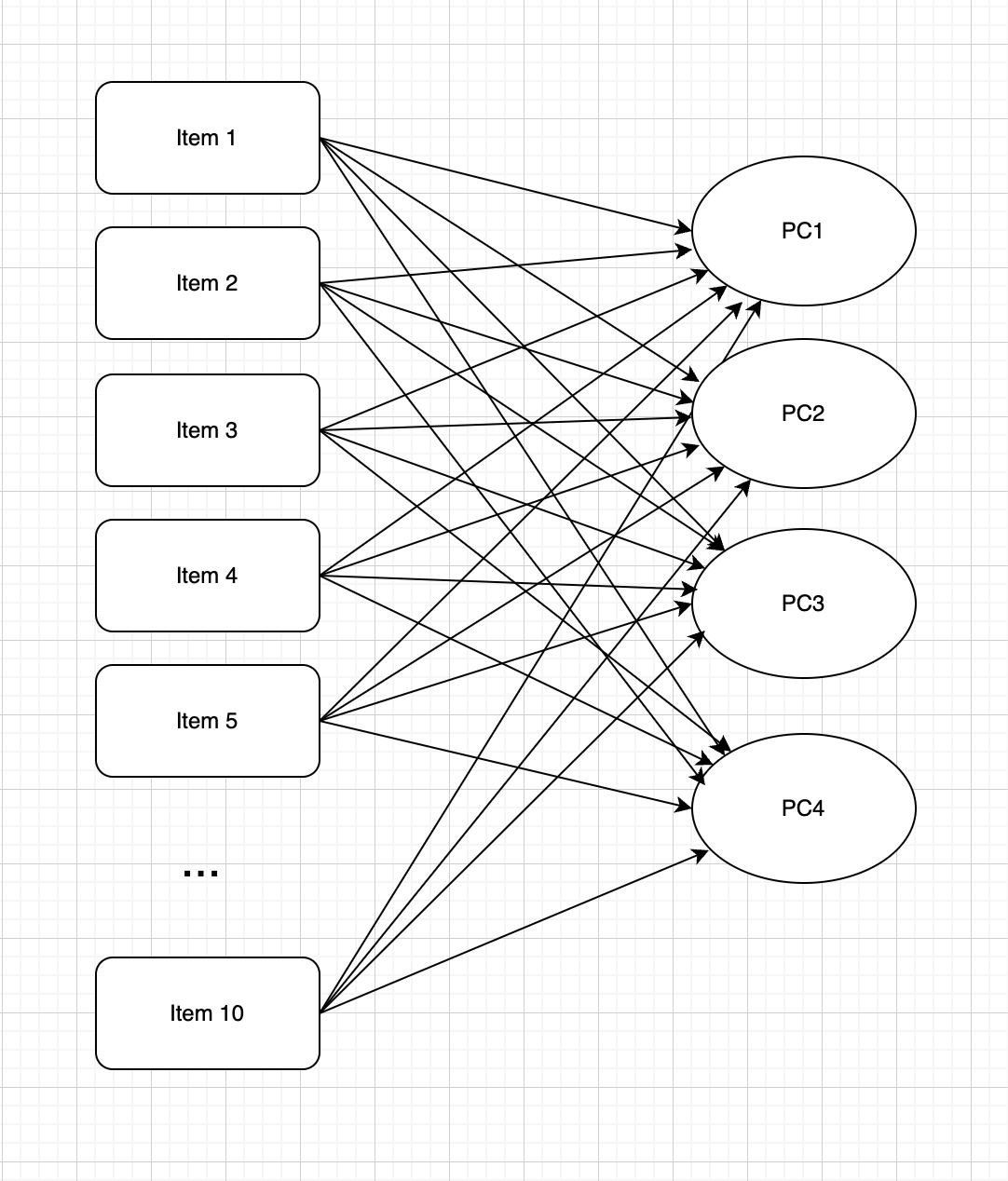
PC: Principal components; Item: Observed variables

Details about the components

The components (\(Z\)) are formed by the weights of the eigenvectors of the covariance or correlation matrix of the original data
- The variance of a component is given by the eigenvalue associated with the eigenvector for the component
Using the eigenvalue and eigenvectors means:
- Each successive component has lower variance
  - Var(Z1) > Var(Z2) > … > Var(Zv)
- All components are uncorrelated
- The sum of the variances of the principal components is equal to the total variance:
\[ \sum_{v=1}^{V} \operatorname{Var}\left(Z_{v}\right)=\operatorname{tr} \mathbf{\Sigma}=\sum_{v=1}^{V} \lambda_{v} \]

PCA on our example

We will now conduct a PCA on the correlation matrix of our sample data
- This example is given for demonstration purposes – typically we will not do PCA on small numbers of variables (> 20 variables?)

PCA in R

The R function that does principal components is called prcomp()

data01 <- dataSAT[, c("SATV", "SATM")]
# PCA of correlation matrix 
sat_pca_corr = prcomp(x = data01, scale. = TRUE)

# show the results
sat_pca_corr

Standard deviations (1, .., p=2):
[1] 1.3323753 0.4741057

Rotation (n x k) = (2 x 2):
            PC1        PC2
SATV -0.7071068  0.7071068
SATM -0.7071068 -0.7071068

# show the summary statistics
summary(sat_pca_corr)

Importance of components:
                          PC1    PC2
Standard deviation     1.3324 0.4741
Proportion of Variance 0.8876 0.1124
Cumulative Proportion  0.8876 1.0000

Graphical Representation

Plotting the components and the original data side by side reveals the nature of PCA:
- Shown from PCA of covariance matrix
- PC I (Principal component I) is uncorrelated to PC II

Code

#create same analysis but with covariance matrix (for visual) scale.=FALSE (covariance matrix) 
sat_pca_cov = prcomp(x = data01, scale. = FALSE)

#create augmented data matrix for plot
data01a = data01
data01a$type = "Raw"

data01b = data.frame(SATV = sat_pca_cov$x[,1], SATM = sat_pca_cov$x[,2], type="PC")
data01c = rbind(data01a, data01b)

plot(x = data01c$SATV, y = data01c$SATM, ylab = "SATM/PC2", xlab = "SATV/PC1", cex.main=1.5, frame.plot=FALSE, col=ifelse(data01c$type=="Raw", "red", "blue"))
legend(0, 400, pch=1, col=c("red", "blue"), c("Data", "PCs"), bty="o",  box.col="darkgreen", cex=1.5)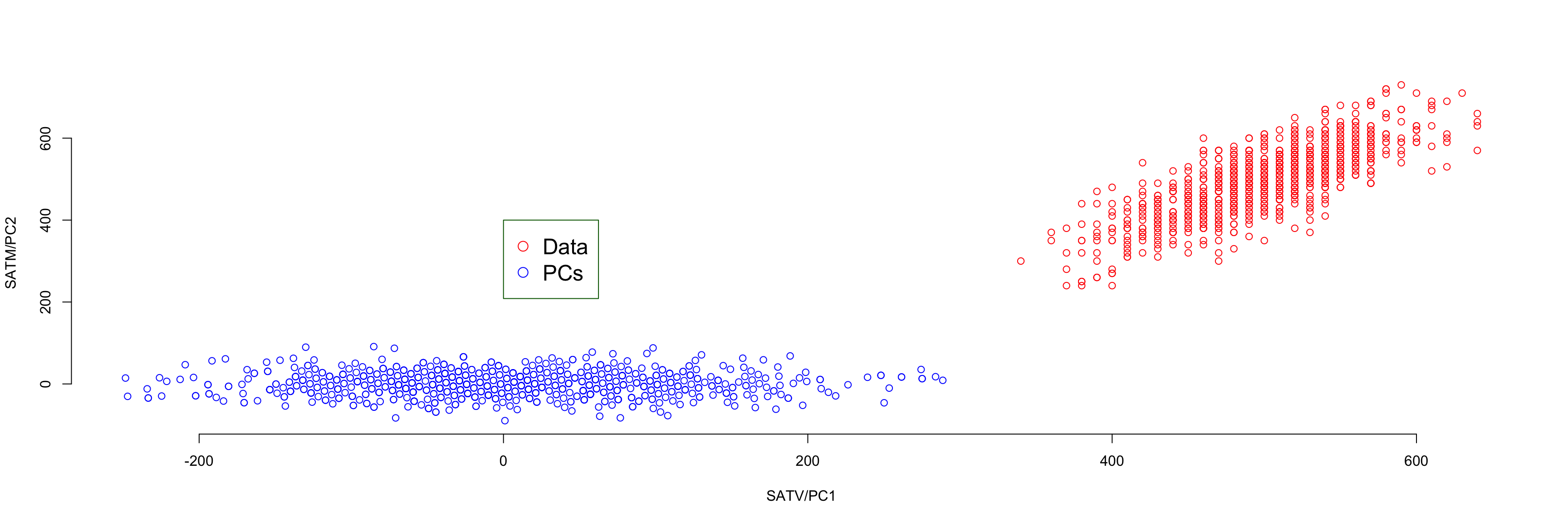

An empirical example: The Growth of Gambling Access

Background:
- In past 25 years, an exponential increase in the accessibility of gambling
- An increased rate of with problem or pathological gambling (Volberg, 2002; Welte et al., 2009)
Hence, there is a need to better:
- Understand the underlying causes of the disorder
- Reliably identify potential pathological gamblers
- Provide effective treatment interventions

Pathological Gambling: DSM Definition

To be diagnosed as a pathological gambler, an individual must meet 5 of 10 defined criteria:

Is preoccupied with gambling
Needs to gamble with increasing amounts of money in order to achieve the desired excitement
Has repeated unsuccessful efforts to control, cut back, or stop gambling
Is restless or irritable when attempting to cut down or stop gambling
Gambles as a way of escaping from problems or relieving a dysphoric mood

After losing money gambling, often returns another day to get even (“chasing” one’s losses)
Lies to family members, therapist, or others to conceal the extent of involvement with gambling
Has committed illegal acts such as forgery, fraud, theft, or embezzlement to finance gambling
Has jeopardized or lost a significant relationship, job, or educational or career opportunity because of gambling
Relies on others to provide money to relieve a desperate financial situation caused by gambling

Research on Pathological Gambling

In order to study the etiology of pathological gambling, more variability in responses was needed
The Gambling Research Instrument (GRI; Feasel, Henson, & Jones,2002) was created with 41 Likert-type items
- Items were developed to measure each criterion
Example items (ratings: Strongly Disagree to Strongly Agree):
- I worry that I am spending too much money on gambling (C3)
- There are few things I would rather do than gamble (C1)
The instrument was used on a sample of experienced gamblers from a riverboat casino in a Flat Midwestern State
- Casino patrons were solicited after playing roulette

The GRI Items

The Gambling Research Instrument (GRI) used a 6-point Likert scale:
- 1: Strongly Disagree
- 2: Disagree
- 3: Slightly Disagree
- 4: Slightly Agree
- 5: Agree
- 6: Strongly Agree
To meet the assumptions of factor analysis, we will treat these responses as being continuous
- This is tenuous at best, but often is the case in factor analysis
- Categorical items would be better….but you’d need another course for how to do that
  - Hint: Item Response Models

The Sample

Data were collected from two sources:
- 112 “experienced” gamblers
  - Many from an actual casino
- 1192 college students from a “rectangular” midwestern state
  - Many never gambled before

data02 = read.csv(file="gambling_lecture12.csv",header=TRUE)
#listwise removal of missing data (common in PCA -- but still a problem)
data02a = data02[complete.cases(data02),]
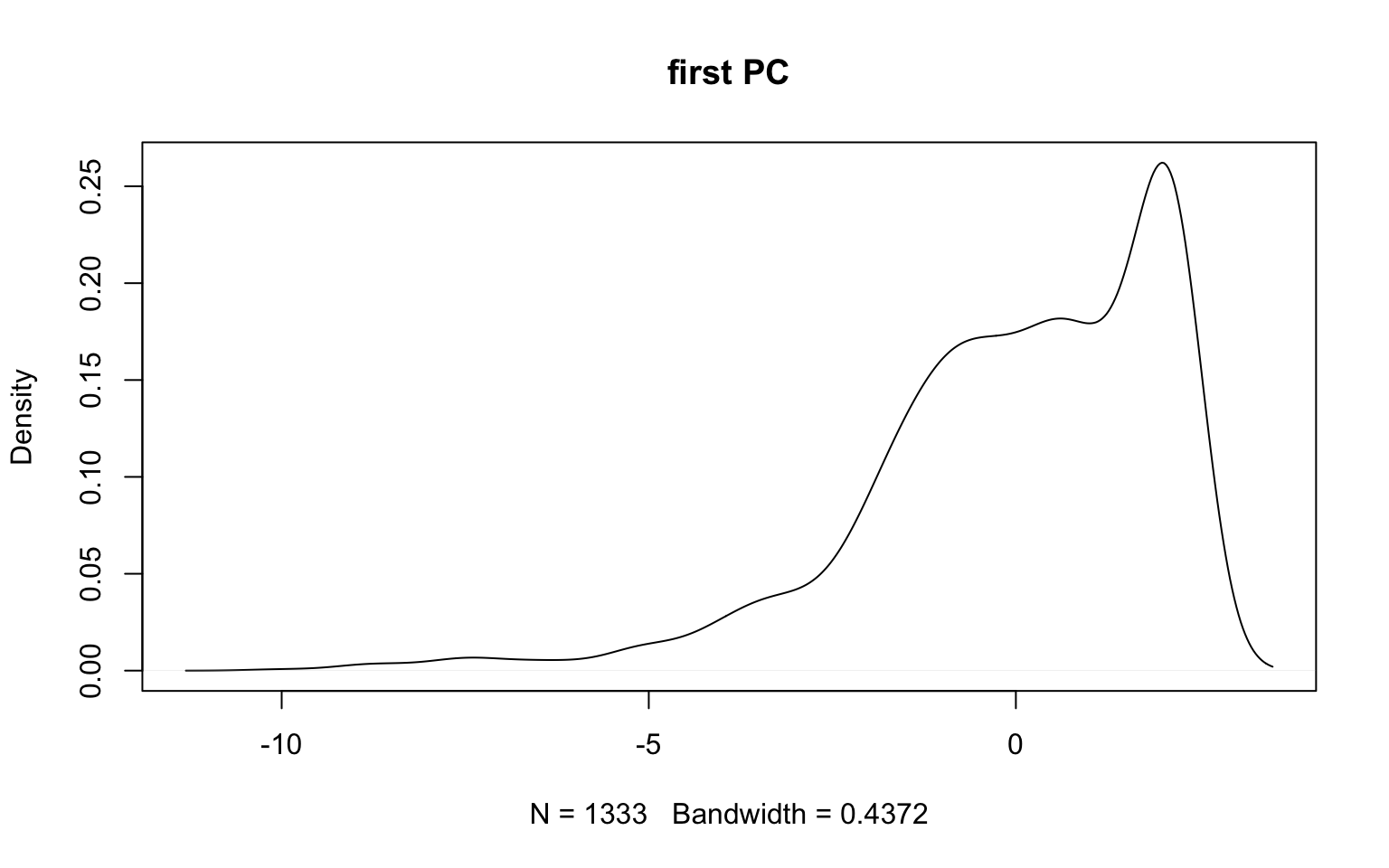
dim(data02a)

[1] 1333   10

Today, we will combine both samples and treat them as homogenous – one sample of 1304 subjects

Final 10 items on the scale

Item	Criterion	Question
GRI1	3	I would like to cut back on my gambling.
GRI3	6	If I lost a lot of money gambling one day, I would be more likely to want to play again the following day.
GRI5	2	I find it necessary to gamble with larger amounts of money (than when I first gambled) for gambling to be exciting.
GRI9	4	I feel restless when I try to cut down or stop gambling.
GRI10	1	It bothers me when I have no money to gamble.
GRI13	3	I find it difficult to stop gambling.
GRI14	2	I am drawn more by the thrill of gambling than by the money I could win.
GRI18	9	My family, coworkers, or others who are close to me disapprove of my gambling.
GRI21	1	It is hard to get my mind off gambling.
GRI23	5	I gamble to improve my mood.

Question #1: How Many Components?

To answer the question of how many components, two methods are used:
- Scree plot of eigenvalues (looking for the “elbow”)
- Variance accounted for (should be > 70%)
We will go with 4 components: (variance accounted for VAC = 75%)
Variance accounted for is for the total sample variance

#analysis of covariance matrix of gambling data items
gambling_pca_cov = prcomp(x = data02a, scale. = FALSE) 
# gambling_pca_cov
summary(gambling_pca_cov)

Importance of components:
                          PC1    PC2    PC3     PC4     PC5     PC6     PC7
Standard deviation     2.0485 1.3229 1.0883 0.83608 0.75096 0.73365 0.68616
Proportion of Variance 0.4043 0.1686 0.1141 0.06736 0.05434 0.05186 0.04537
Cumulative Proportion  0.4043 0.5730 0.6871 0.75447 0.80881 0.86067 0.90604
                           PC8     PC9    PC10
Standard deviation     0.64836 0.58230 0.46438
Proportion of Variance 0.04051 0.03267 0.02078
Cumulative Proportion  0.94655 0.97922 1.00000

Plots to Answer How Many Components

Code

prop_var = t(summary(gambling_pca_cov)$importance[2:3,])
#creating a scree plot and a proportion of variance plot

par(mfrow = c(1,2))
plot(gambling_pca_cov, type="l", main = "Scree Plot of PCA Eigenvalues", lwd = 5)
matplot(prop_var, type="l", main = "Proportion of Variance Explained by Component", lwd = 5)
legend(x=5, y=.5, legend = c("Component Variance", "Cumulative Variance"), lty = 1:2, lwd=5, col=1:2)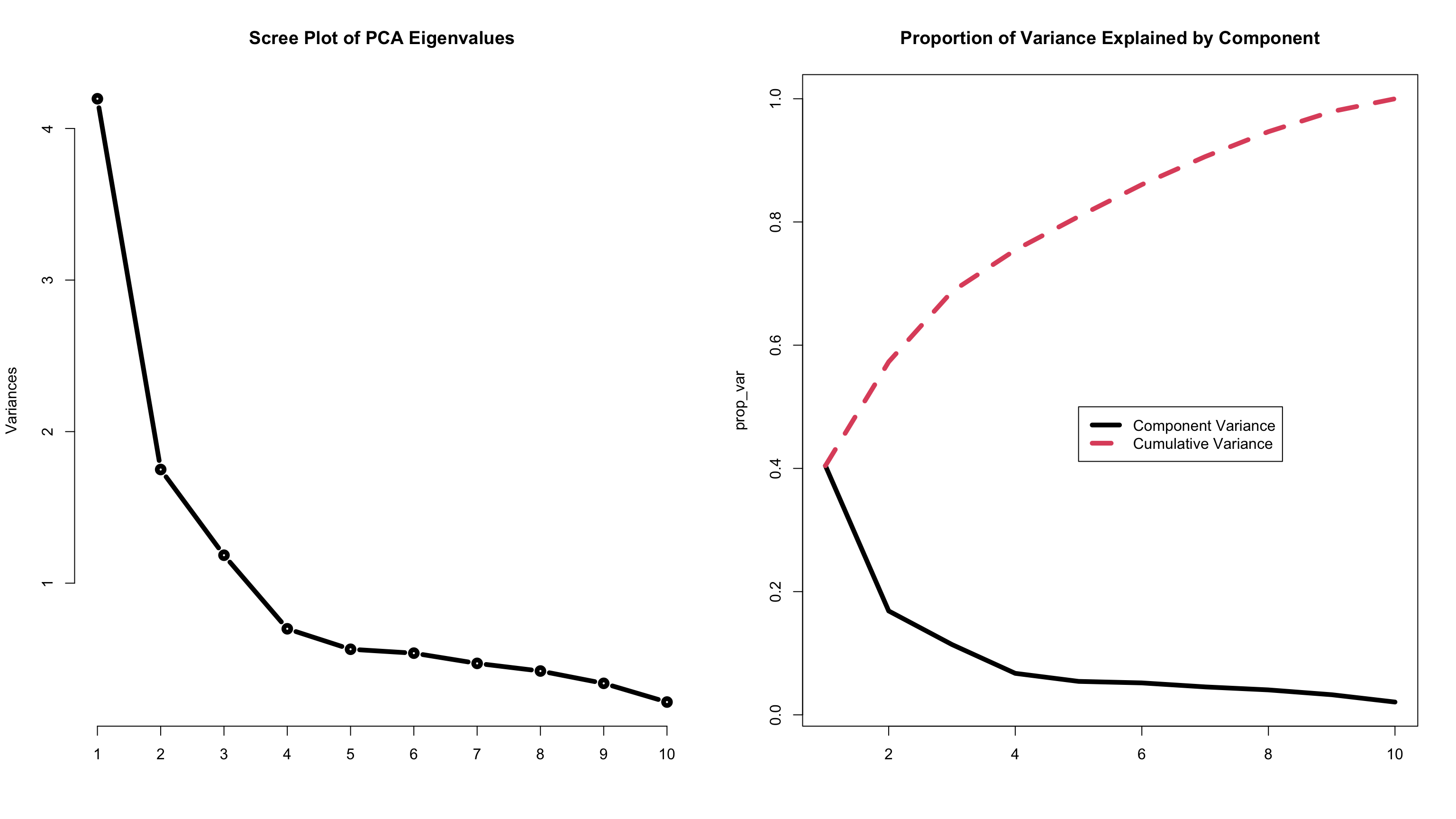

Question #2: What Does Each Component Represent?

To answer question #2 – we look at the weights of the eigenvectors (here is the unrotated solution)

round(gambling_pca_cov$rotation, 3)

       PC1    PC2    PC3    PC4    PC5    PC6    PC7    PC8    PC9   PC10
X1  -0.313  0.105  0.166 -0.844  0.365 -0.090  0.090  0.002  0.028  0.040
X3  -0.226  0.078  0.178 -0.134 -0.525  0.680  0.343 -0.192 -0.015  0.026
X5  -0.320  0.094  0.229  0.026 -0.492 -0.626 -0.090 -0.395 -0.044  0.187
X9  -0.243  0.087  0.160  0.031 -0.117 -0.062 -0.153  0.152  0.045 -0.917
X10 -0.280  0.087  0.235  0.085 -0.195 -0.026 -0.093  0.842 -0.027  0.307
X13 -0.329  0.156  0.186  0.220  0.326  0.295 -0.505 -0.225 -0.524  0.101
X14 -0.449 -0.862 -0.231  0.006 -0.004  0.026 -0.037 -0.001 -0.004  0.002
X18 -0.347  0.405 -0.834 -0.028 -0.100 -0.019  0.009  0.053 -0.074  0.002
X21 -0.272  0.137  0.062  0.198  0.179  0.155 -0.250 -0.143  0.842  0.128
X23 -0.326  0.098  0.139  0.416  0.386 -0.147  0.718 -0.025 -0.071 -0.033

Given 10-item survey, we can extract 10 components at most, but we only use first 4 principal components. They are enough to explain the total variance of data.

Final Result: Four Principal Components

Using the weights of the eigenvectors, we can create four new variables – the four principal components
Strong assumption: Each of these is uncorrelated with each other
- The variance of each is equal to the corresponding eigenvalue
We would then use these in subsequent analyses

head(gambling_pca_cov$x[, 1:4], 5)

         PC1       PC2       PC3        PC4
1 -2.5448889 1.2879590 1.5823332 -1.8230315
2  2.1851408 0.3646125 0.1984711  0.2642768
3 -0.6179050 0.6644431 0.2403178  0.3784284
4  0.1443078 1.1269409 1.5393139 -0.1311429
5  0.1443078 1.1269409 1.5393139 -0.1311429

plot(density(gambling_pca_cov$x[, 1]), 
     main = "first PC")

PCA Summary

PCA is a data reduction technique that relies on the mathematical properties of eigenvalues and eigenvectors
- Used to create new variables (small number) out of the old data (lots of variables)、
- The new variables are principal components (they are not factor scores)
PCA appeared first in the psychometric literature
- Many “factor analysis” methods used variants of PCA before likelihood-based statistics were available
Currently, PCA (or variants) methods are the default option in SPSS and SAS (PROC FACTOR)

Potentially Solvable Statistical Issues in PCA

The typical PCA analysis also has a few statistical concerns
- Some of these can be solved if you know what you are doing
- The typical analysis (using program defaults) does not solve these
Missing data is omitted using listwise deletion – biases possible
- Could use ML to estimate covariance matrix, but then would have to assume multivariate normality
- Could use MI to impute data
The distributions of variables can be anything…but variables with much larger variances will look like they contribute more to each component
- Could standardize variables – but some can’t be standardized easily (think gender)
The lack of standard errors makes the component weights (eigenvector elements) hard to interpret
- Can use a resampling/bootstrap analysis to get SEs (but not easy to do)

(Unsolvable) Issues with PCA

My issues with PCA involve the two questions in need of answers for any use of PCA:

The number of components needed is not based on a statistical hypothesis test and hence is subjective
- Variance accounted for is a descriptive measure
- No statistical test for whether an additional component significantly accounts for more variance
The relative meaning of each component is questionable at best and hence is subjective
- Typical packages provide no standard errors for each eigenvector weight (can be obtained in bootstrap analyses)
- No definitive answer for component composition

In sum, I feel it is very easy to be misled (or purposefully mislead) with PCA

EXPLORATORY FACTOR ANALYSIS (EFA)

Primary Purpose of EFA

EFA: “Determine nature and number of latent variables that account for observed variation and covariation among set of observed indicators (≈ items or variables)”
- In other words, what causes these observed responses?
- Summarize patterns of correlation among indicators
- Solution is an end (i.e., is of interest) in and of itself
Compared with PCA: “Reduce multiple observed variables into fewer components that summarize their variance”
- In other words, how can I abbreviate this set of variables?
- Solution is usually a means to an end

Methods for EFA

You will see many different types of methods for “extraction” of factors in EFA
- Many are PCA-based
- Most were developed before computers became relevant or likelihood theory was developed
You can ignore all of them and focus on one:
- Only use Maximum Likelihood method for EFA
The maximum likelihood method of EFA extraction:
- Uses the same log-likelihood as confirmatory factor analyses/SEM
  - Default assumption: multivariate normal distribution of data
- Provides consistent estimates with good statistical properties (assuming you have a large enough sample)
- Missing data using all the data that was observed (MAR)
- Is consistent with modern statistical practices

Questions when using EFA

EFAs proceed by seeking the answers to two questions: (the same questions posed in PCA; but with different terms)
1. How many latent factors are needed to “adequately” represent the original data?
  - “Adequately” = does a given EFA model fit well?
2. (once #1 has been answered): What does each factor represent?
  - The term “represent” is fuzzy

The Syntax of Factor Analysis

Factor analysis works by hypothesizing that a set of latent factors helps to determine a person’s response to a set of variables
- This can be explained by a system of simultaneous linear models
- Here Y = observed data, p = person, v = variable, F = factor score (Q factors)

\[ \begin{array}{c} Y_{p 1}=\mu_{y_{1}}+\lambda_{11} F_{p 1}+\lambda_{12} F_{p 2}+\cdots+\lambda_{1 Q} F_{p Q}+e_{p 1} \\ Y_{p 2}=\mu_{y_{2}}+\lambda_{21} F_{p 1}+\lambda_{22} F_{p 2}+\cdots+\lambda_{2 Q} F_{p Q}+e_{p 2} \\ \vdots \\ Y_{p V}=\mu_{y_{V}}+\lambda_{V 1} F_{p 1}+\lambda_{V 2} F_{p 2}+\cdots+\lambda_{V Q} F_{p Q}+e_{p V} \end{array} \]

\(\mu_{y_v}\) = mean for variable \(v\);
\(\lambda_{vq}\) = factor loading for variable v onto factor f (regression slope)
- Factors are assumed distributed MVN with zero mean and (for EFA) identity covariance matrix (uncorrelated factors – to start)
\(e_{pv}\) = residual for person p and variable v;
- Residuals are assumed distributed MVN (across items) with a zero mean and a diagonal covariance matrix \(\mathbf\Psi\) containing the unique variances
Often, this gets shortened into matrix form:

\[ \mathbf{Y_p = \mu_Y+\Lambda F_p^T + e_p} \]

Diagram of EFA

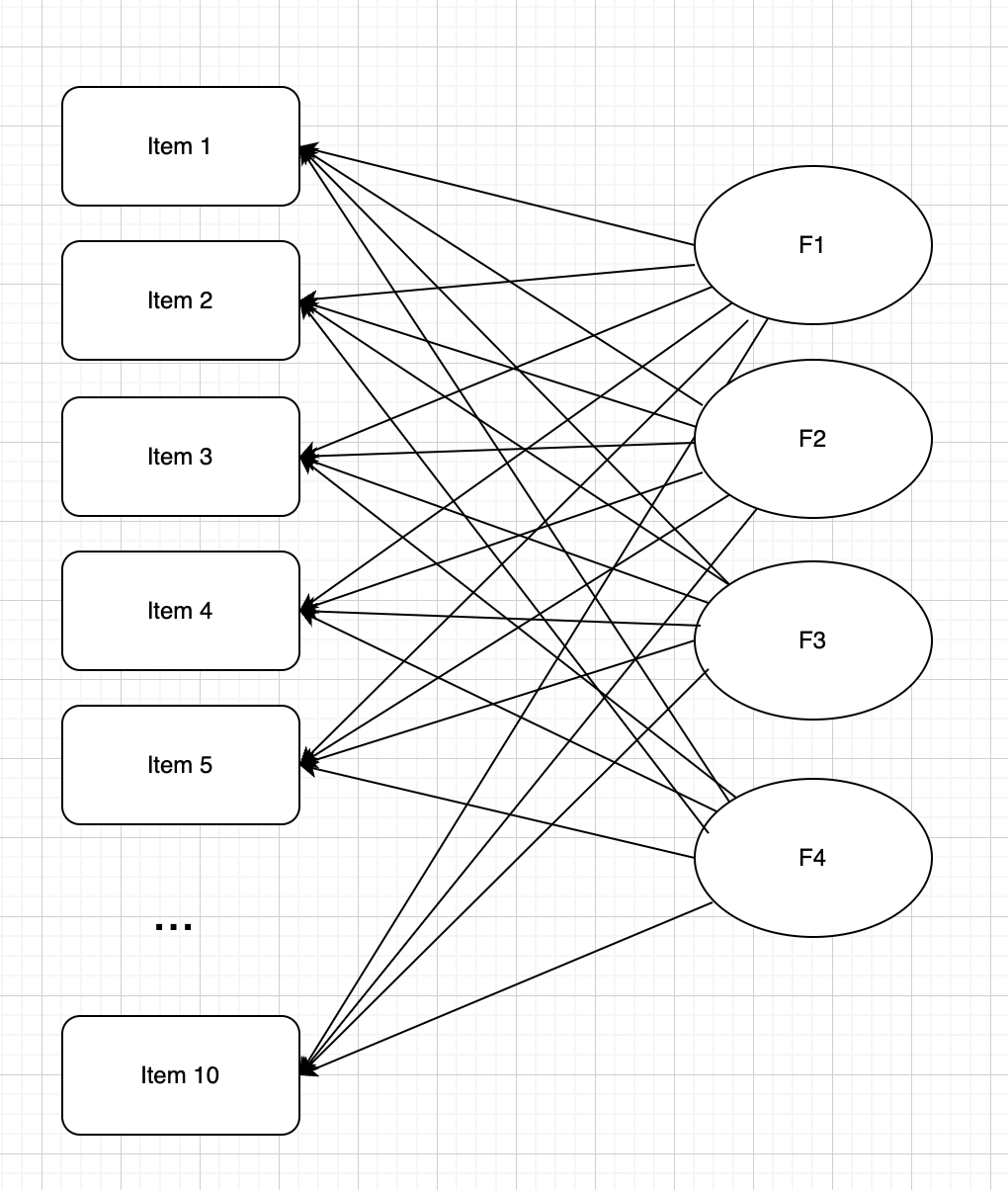
Latent factors are common factors of observed variables

How Maximum Likelihood EFA Works

Maximum likelihood EFA assumes the data follow a multivariate normal distribution
- The basis for the log-likelihood function (same log-likelihood we have used in every analysis to this point)
The log-likelihood function depends on two sets of parameters: the mean vector and the covariance matrix
- Mean vector is saturated (just uses the item means for item intercepts) – so it is often not thought of in analysis
  - Denoted as \(\boldsymbol\mu_y = \boldsymbol\mu_I\)
- Covariance matrix is what gives “factor structure”
  - EFA models provide a structure for the covariance matrix

The EFA Model for the Covariance Matrix

The covariance matrix is modeled based on how it would look if a set of hypothetical (latent) factors had caused the data
For an analysis measuring \(F\) factors, each item in the EFA:
- Has 1 unique variance parameter
- Has F factor loadings
The initial estimation of factor loadings is conducted based on the assumption of uncorrelated factors
- Assumption is dubious at best – yet is the cornerstone of the analysis

Model Implied Covariance Matrix

The factor model implied covariance matrix is \(\boldsymbol{\Sigma_Y=\Lambda\Phi\Lambda^T+\Psi}\)
- Where:
  - \(\boldsymbol{\Sigma_Y}\) = model implied covariance matrix of the observed data (size \(I \times I\))
  - \(\boldsymbol{\Lambda}\) = matrix of factor loadings (size \(I \times F\))
    - In EFA: all terms in \(\boldsymbol{\Lambda}\) are estimated
  - \(\boldsymbol{\Phi}\) = factor covariance matrix (size \(F \times F\)) – In EFA: \(\boldsymbol{\Phi}\) = \(\boldsymbol{I}\) (all factors have variances of 1 and covariances of 0)
    - In CFA: this is estimated
  - \(\boldsymbol{\Psi}\) = matrix of unique (residual) variances (size \(I \times I\))
    - In EFA: \(\boldsymbol{\Psi}\) is diagonal by default (no residual covariances)
Therefore, the EFA model-implied covariance matrix is:

\[ \boldsymbol{\Sigma}_{Y}=\boldsymbol{\Lambda} \mathbf{\Lambda}^{T}+\boldsymbol{\Psi} \]

EFA Model Identifiability

Under the ML method for EFA, the same rules of identification apply to EFA as to Path Analysis
- T-rule: Total number of EFA model parameters must not exceed unique elements in saturated covariance matrix of data
  - For an analysis with a number of factors \(F\) and a set number of items \(I\) there are \(F*I+I=I(F+1)\) EFA model parameters
  - As we will see, there must be \(\frac{F(F-1)}{2}\) constraints for the model to work
  - Therefore, \(I(F+1)-\frac{F(F-1)}{2}<\frac{I(I+1)}{2}\)
- Local identification: each portion of the model must be locally identified
  - With all factor loadings estimated local identification fails
    - No way of differentiating factors without constraints

Constraints to Make EFA in ML Identified

The EFA model imposes the following constraint: \[ \mathbf{\Lambda^T\Psi\Lambda=\Delta} \]

such that \(\mathbf\Delta\) is a diagonal matrix

This puts \(\frac{F(F-1)}{2}\) constraints on the model (that many fewer parameters to estimate).
This constraint is not well known – and how it functions is hard to describe
- For a 1-factor model, the results of EFA and CFA will match
Note: the other methods of EFA “extraction” avoid this constraint by not being statistical models in the first place
- PCA-based routines rely on matrix properties to resolve identification

The Nature of the Constraints in EFA

The EFA constraints provide some detailed assumptions about the nature of the factor model and how it pertains to the data
For example, take a 2-factor model (one constraint):

\[ \sum_{v=1}^{V} \psi_{v}^{2} \prod_{f=1}^{Q=2} \lambda_{v f}=0 \]

In short, some combinations of factor loadings and unique variances (across and within items) cannot happen
- This goes against most of our statistical constraints – which must be justifiable and understandable (therefore testable)
- This constraint is not testable in CFA

Benefits and Consequences of EFA with ML

The parameters of the EFA model under ML retain the same benefits and consequences of any model (i.e., CFA)
- Asymptotically (large N) they are consistent, normal, and efficient
- Missing data are “skipped” in the likelihood, allowing for incomplete observations to contribute (assumed MAR)
Furthermore, the same types of model fit indices are available in EFA as are in CFA
As with CFA, though, an EFA model must be a close approximation to the saturated model covariance matrix if the parameters are to be believed

ML-based EFA Using the `factanal()` Function

The base R program has the factanal() function that conducts ML-based EFA
Although the function use ML, you still cannot have missing data in the analysis based of the limitations of factanal function
- Thus, we will remove cases with any missing data (listwise deletion) and proceed
We will also not use a rotation method at first as to show how default constraints in EFA with ML are ridiculous

Step 1: Determine Number of Factors

The EFA factanal() function provides a rudimentary test for model fit

#one-factor model
EFA_1factor = factanal(x = data02a, factors = 1, rotation = "none")
EFA_1factor


Call:
factanal(x = data02a, factors = 1, rotation = "none")

Uniquenesses:
   X1    X3    X5    X9   X10   X13   X14   X18   X21   X23 
0.677 0.728 0.550 0.417 0.527 0.488 0.857 0.816 0.538 0.573 

Loadings:
    Factor1
X1  0.569  
X3  0.521  
X5  0.670  
X9  0.764  
X10 0.688  
X13 0.715  
X14 0.378  
X18 0.429  
X21 0.680  
X23 0.653  

               Factor1
SS loadings      3.828
Proportion Var   0.383

Test of the hypothesis that 1 factor is sufficient.
The chi square statistic is 161.14 on 35 degrees of freedom.
The p-value is 4.23e-18

Remember the saturated model from path analysis?
- All covariances estimated
The model fit tests the solution from EFA vs the saturated model
- EFA 1-factor model shown
The goal is to find a model that fits well

A quick example using EFA

Step 1: Select Best Model: Chi-square

chi_sq_test <- function(mod) {
  num_factor <- mod$factors
  chi_stat <- round(mod$STATISTIC, 3)
  dof <- mod$dof
  p_value <- round(mod$PVAL, 4)
  print(glue::glue("{num_factor}-factor model: The chi square statistic is {chi_stat} on {dof} degrees of freedom. The p-value is {p_value}"))
}

#one-factor model
EFA_1factor = factanal(x = data02a, factors = 1, rotation = "none")
chi_sq_test(EFA_1factor)

#two-factor model
EFA_2factor = factanal(x = data02a, factors = 2, rotation = "none")
chi_sq_test(EFA_2factor)

#three-factor model
EFA_3factor = factanal(x = data02a, factors = 3, rotation = "none")
chi_sq_test(EFA_3factor)

#four-factor model
EFA_4factor = factanal(x = data02a, factors = 4, rotation = "none")
chi_sq_test(EFA_4factor)

1-factor model: The chi square statistic is 161.138 on 35 degrees of freedom. The p-value is 0
2-factor model: The chi square statistic is 56.428 on 26 degrees of freedom. The p-value is 5e-04
3-factor model: The chi square statistic is 31.235 on 18 degrees of freedom. The p-value is 0.027
4-factor model: The chi square statistic is 10.2 on 11 degrees of freedom. The p-value is 0.5125

Step 2: Interpreting the Best Model

As the four-factor solution fit best, we will interpret it
Unrotated solution of factor loadings:

EFA_4factor$loadings


Loadings:
    Factor1 Factor2 Factor3 Factor4
X1   0.356   0.457   0.127   0.346 
X3   0.322   0.403                 
X5   0.452   0.480   0.174         
X9   0.468   0.630   0.196  -0.144 
X10  0.458   0.502   0.186         
X13  0.509   0.494                 
X14  0.292   0.227                 
X18  0.316   0.294  -0.141   0.128 
X21  0.491   0.548  -0.408         
X23  0.997                         

               Factor1 Factor2 Factor3 Factor4
SS loadings      2.542   1.933   0.327   0.183
Proportion Var   0.254   0.193   0.033   0.018
Cumulative Var   0.254   0.447   0.480   0.499

F1 has the most number of relationships with all items of gambling (general gambling level?), followed by F2 (special type of gambling?), F3, and F4. It is very difficult to know what each factor really means.

Step 3: Rotations of Factor Loadings in EFA

Transformations of the factor loadings are possible as the matrix of factor loadings is only unique up to an orthogonal transformation
Historically, rotations use the properties of matrix algebra to adjust the factor loadings to more interpretable numbers
Modern versions of rotations/transformations rely on “target functions” that specify what a “good” solution should look like

Step 3: Types of Classical Rotated Solutions

Multiple types of rotations exist but two broad categories seem to dominate how they are discussed:
Orthogonal rotations: rotations that force the factor correlation to zero (orthogonal factors). The name orthogonal relates to the angle between axes of factor solutions being 90 degrees. The most prevalent is the varimax rotation.
Oblique rotations: rotations that allow for non-zero factor correlations. The name orthogonal relates to the angle between axes of factor solutions not being 90 degrees. The most prevalent is the promax rotation.
- These rotations provide an estimate of “factor correlation”

Step 3: How Classical Orthogonal Rotation Works

Classical orthogonal rotation algorithms work by defining a new rotated set of factor loadings 𝚲∗ as a function of the original (non-rotated) loadings \(\mathbf\Lambda\) and an orthogonal rotation matrix \(\mathbf T\)

\[ \mathbf{\Lambda}^{*}=\boldsymbol{\Lambda} \mathbf{T} \]

where: \(\mathbf {TT^T=T^TT = I}\)

\[ \begin{array}{l} \boldsymbol{\Sigma}_{Y}=\boldsymbol{\Lambda}^{*} \boldsymbol{\Lambda}^{* T}+\boldsymbol{\Psi}=\boldsymbol{\Lambda} \mathbf{T}(\boldsymbol{\Lambda} \mathbf{T})^{T}+\boldsymbol{\Psi}=\boldsymbol{\Lambda} \mathbf{T T}^{T} \boldsymbol{\Lambda}^{T}+\boldsymbol{\Psi} \\ =\boldsymbol{\Lambda} \boldsymbol{\Lambda}^{T}+\boldsymbol{\Psi} \end{array} \]

Rotation Algorithms

Given a target function, rotation algorithms seek to find a rotated solution that simultaneously:
- Minimizes the distance between the rotated solution and the original factor loadings
- Fits best to the target function

Example: Orthogonal Rotation via Varimax

no factor correlation

#varimax rotation
EFA_4factor_varimax = factanal(x = data02a, factors = 4, rotation = "varimax")
EFA_4factor_varimax$loadings


Loadings:
    Factor1 Factor2 Factor3 Factor4
X1  0.301   0.209   0.114   0.569  
X3  0.360   0.213   0.113   0.307  
X5  0.532   0.224   0.202   0.301  
X9  0.714   0.291   0.157   0.239  
X10 0.597   0.231   0.202   0.234  
X13 0.414   0.461   0.236   0.268  
X14 0.224   0.129   0.162   0.242  
X18 0.147   0.346   0.144   0.246  
X21 0.300   0.746   0.184   0.166  
X23 0.266   0.270   0.904   0.188  

               Factor1 Factor2 Factor3 Factor4
SS loadings      1.772   1.255   1.086   0.873
Proportion Var   0.177   0.125   0.109   0.087
Cumulative Var   0.177   0.303   0.411   0.499

Example: Oblique Rotation via Promax

It also brought about the following factor correlations:
Each factor explain different sets of items

#promax rotation
EFA_4factor_varimax = factanal(x = data02a, factors = 4, rotation = "promax")
EFA_4factor_varimax$loadings


Loadings:
    Factor1 Factor2 Factor3 Factor4
X1                  -0.104   0.861 
X3   0.249                   0.308 
X5   0.530                   0.171 
X9   0.885                         
X10  0.699                         
X13  0.254           0.368   0.101 
X14                          0.274 
X18 -0.126           0.314   0.269 
X21                  0.906  -0.106 
X23          1.037                 

               Factor1 Factor2 Factor3 Factor4
SS loadings      1.712   1.102   1.072   1.040
Proportion Var   0.171   0.110   0.107   0.104
Cumulative Var   0.171   0.281   0.389   0.493

Wrapping Up

Today we discussed the world of exploratory factor analysis and found the following:
1. PCA is what people typically run before they found EFA
2. ML EFA is a better option to pick (likelihood based)
3. Constraints of EFA employed are hidden!
4. Rotations can break without you realizing they do (cannot interpret the factors)

Lecture 12: Principal Components Analysis and Exploratory Factor Analysis

Course Evaluation

Today’s Class

The Logic of Exploratory Analysis

Advanced Matrix Operations

Matrix Orthogonality

Eigenvalues and Eigenvectors

R Code: Eigenvalues and Eigenvectors

Spectral Decomposition

Additional Eigenvalue Properties

PRINCIPAL COMPONENTS ANALYSIS (PCA)

PCA Overview

Goals of PCA

Questions when using PCA

PCA Features

PCA Formulas

Diagram of PCA

Details about the components

PCA on our example

PCA in R

Graphical Representation

An empirical example: The Growth of Gambling Access

Pathological Gambling: DSM Definition

Research on Pathological Gambling

The GRI Items

The Sample

Final 10 items on the scale

Question #1: How Many Components?

Plots to Answer How Many Components

Question #2: What Does Each Component Represent?

Final Result: Four Principal Components

PCA Summary

Potentially Solvable Statistical Issues in PCA

(Unsolvable) Issues with PCA

EXPLORATORY FACTOR ANALYSIS (EFA)

Primary Purpose of EFA

Methods for EFA

Questions when using EFA

The Syntax of Factor Analysis

Diagram of EFA

How Maximum Likelihood EFA Works

The EFA Model for the Covariance Matrix

Model Implied Covariance Matrix

EFA Model Identifiability

Constraints to Make EFA in ML Identified

The Nature of the Constraints in EFA

Benefits and Consequences of EFA with ML

ML-based EFA Using the factanal() Function

Step 1: Determine Number of Factors

A quick example using EFA

Step 1: Select Best Model: Chi-square

Step 2: Interpreting the Best Model

Step 3: Rotations of Factor Loadings in EFA

Step 3: Types of Classical Rotated Solutions

Step 3: How Classical Orthogonal Rotation Works

Rotation Algorithms

Example: Orthogonal Rotation via Varimax

Example: Oblique Rotation via Promax

Wrapping Up

ML-based EFA Using the `factanal()` Function