Lecture 13: Confirmatory Factor Analysis and Psychological Network

Jihong Zhang

Educational Statistics and Research Methods (ESRM) Program*

University of Arkansas

2024-11-22

Today’s Objectives

1. Understand the relationship between Exploratory and Confirmatory Factor Analysis

2. Understand what is network analysis and confirmatory factor analysis

3. Understand how network model can be applied into real examples

Confirmatory Factor Analysis

CFA Approach to EFA

• EFA and CFA are same things except that one is to explore the factor structure (EFA) and one is to confirm pre-determined factor structure (CFA).

• But … we can also conduct exploratory analysis using a CFA model <<<<<<< HEAD =======

  • Need to set the right number of constraints for identification
  • We set the value of factor loadings for a few items on a few of the factors
    • Typically to zero
    • Sometimes to one (Brown, 2002)
  • We keep the factor covariance matrix as an identity
    • Uncorrelated factors (as in EFA) with variances of one

• Benefits of using CFA for exploratory analyses:

  • CFA constraints remove rotational indeterminacy of factor loadings – no rotating is needed (or possible)
  • Defines factors with potentially less ambiguity
    • Constraints are easy to see
    • For some software (SAS and SPSS), we get much more model fit information
  • For some software (SAS and SPSS), we get much more model fit information

CFA Example

• We can use lavaan to do CFA… here is the syntax for the one factor model
  • The ~= is the symbol represent factors and their loaded items
• We can see that the one-factor CFA has same loading with EFA

library(lavaan)
data02a = read.csv(file="gambling_lecture12.csv", header=TRUE)
head(data02a, 3)

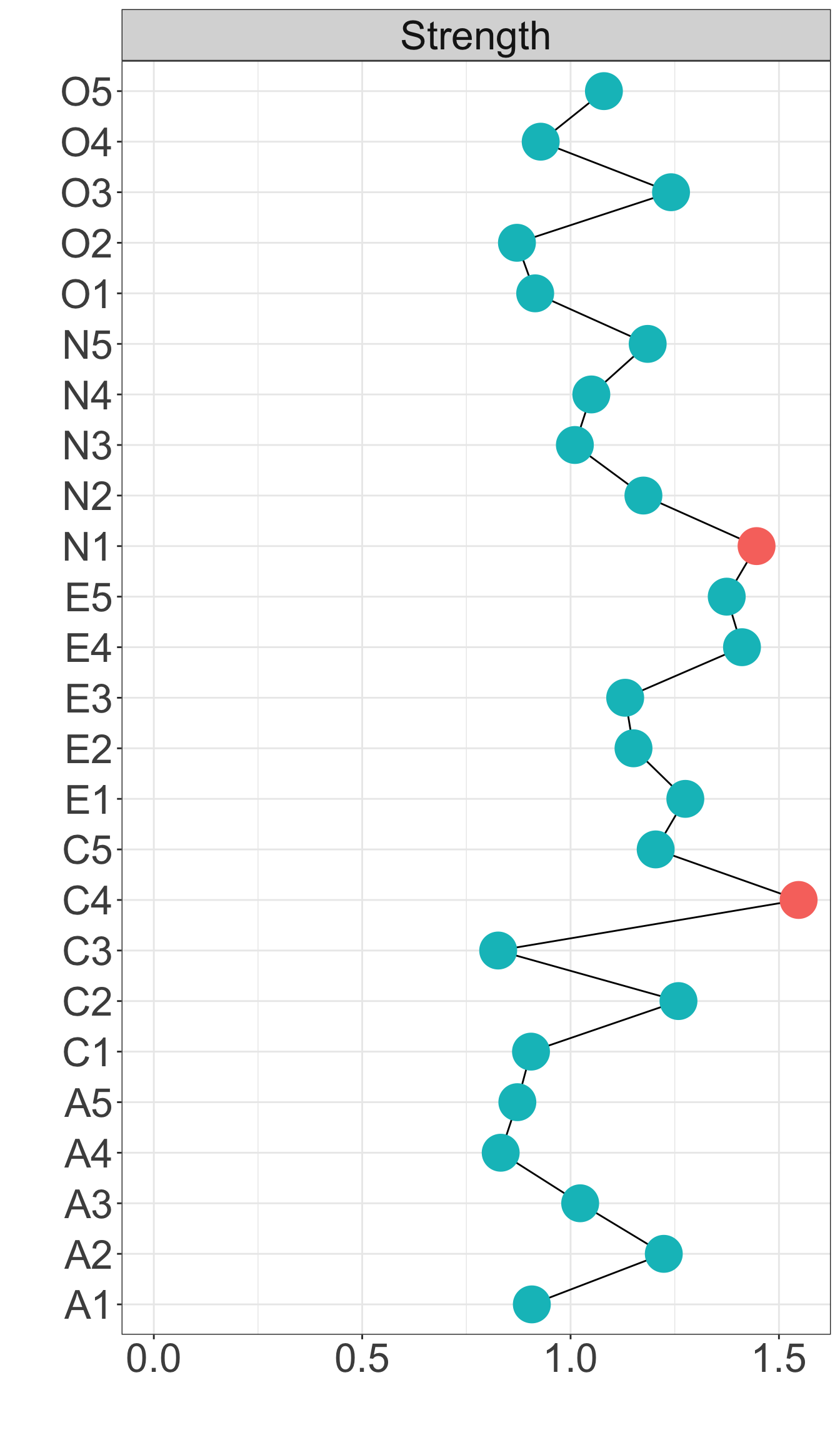
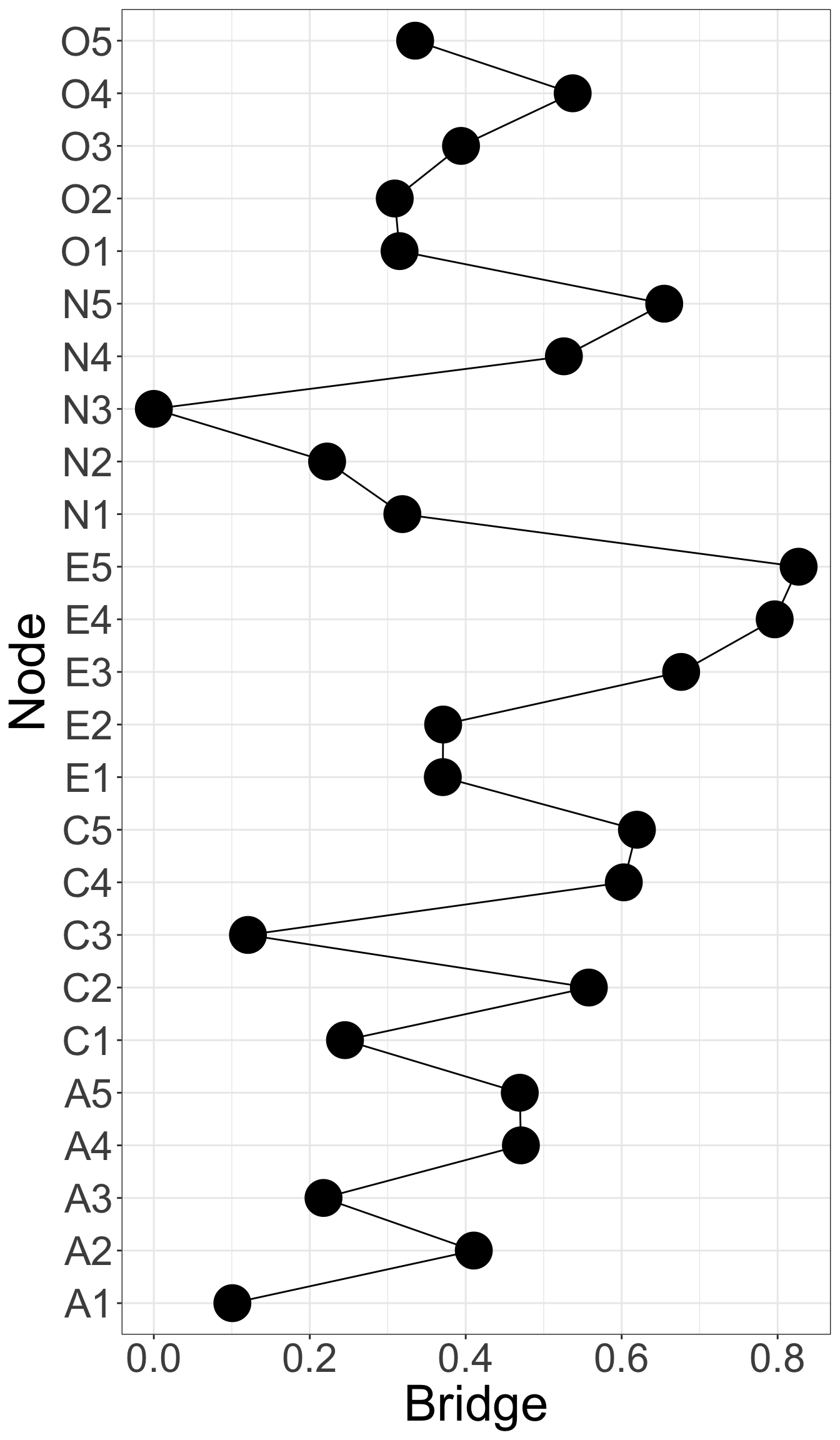
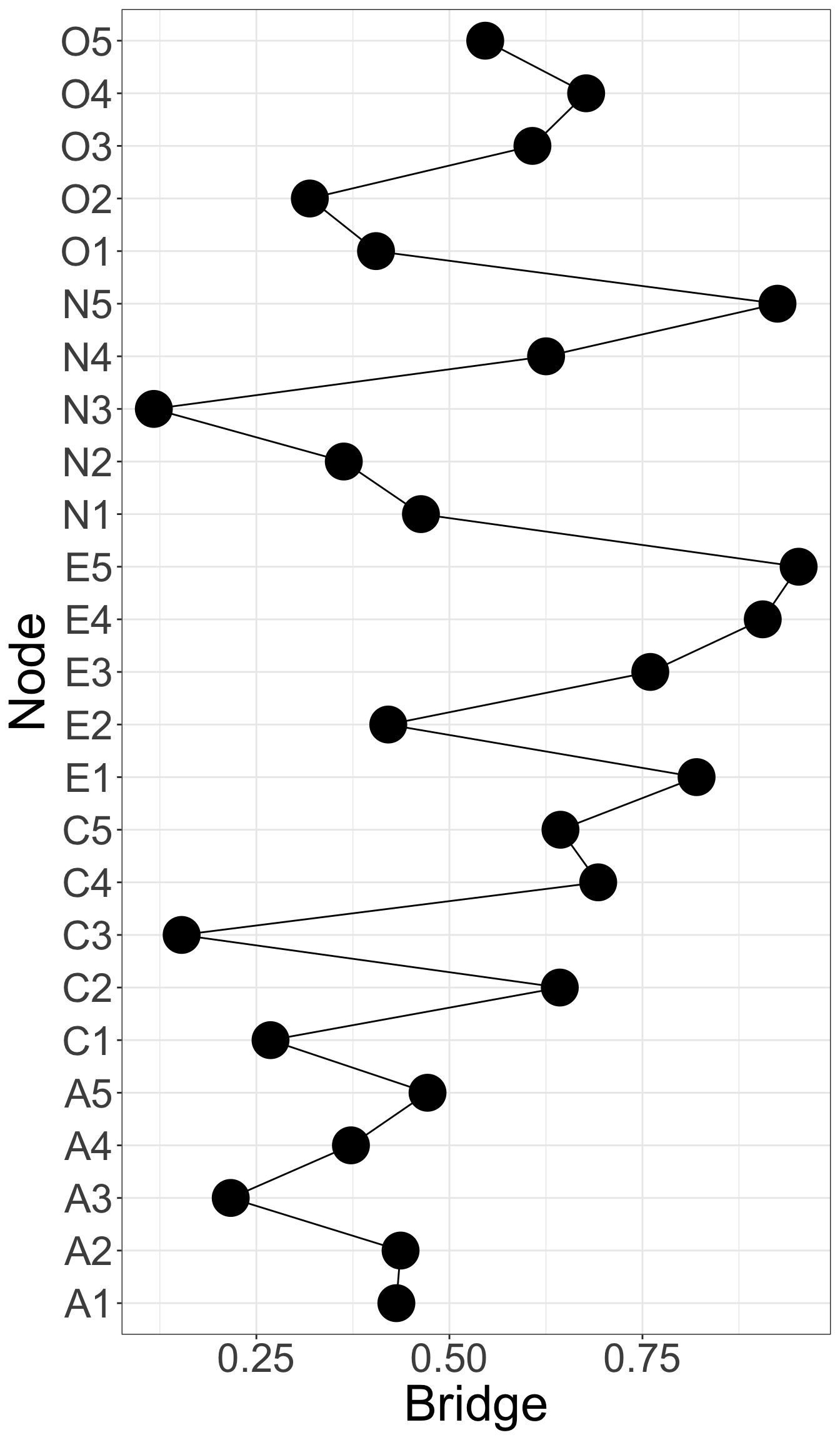
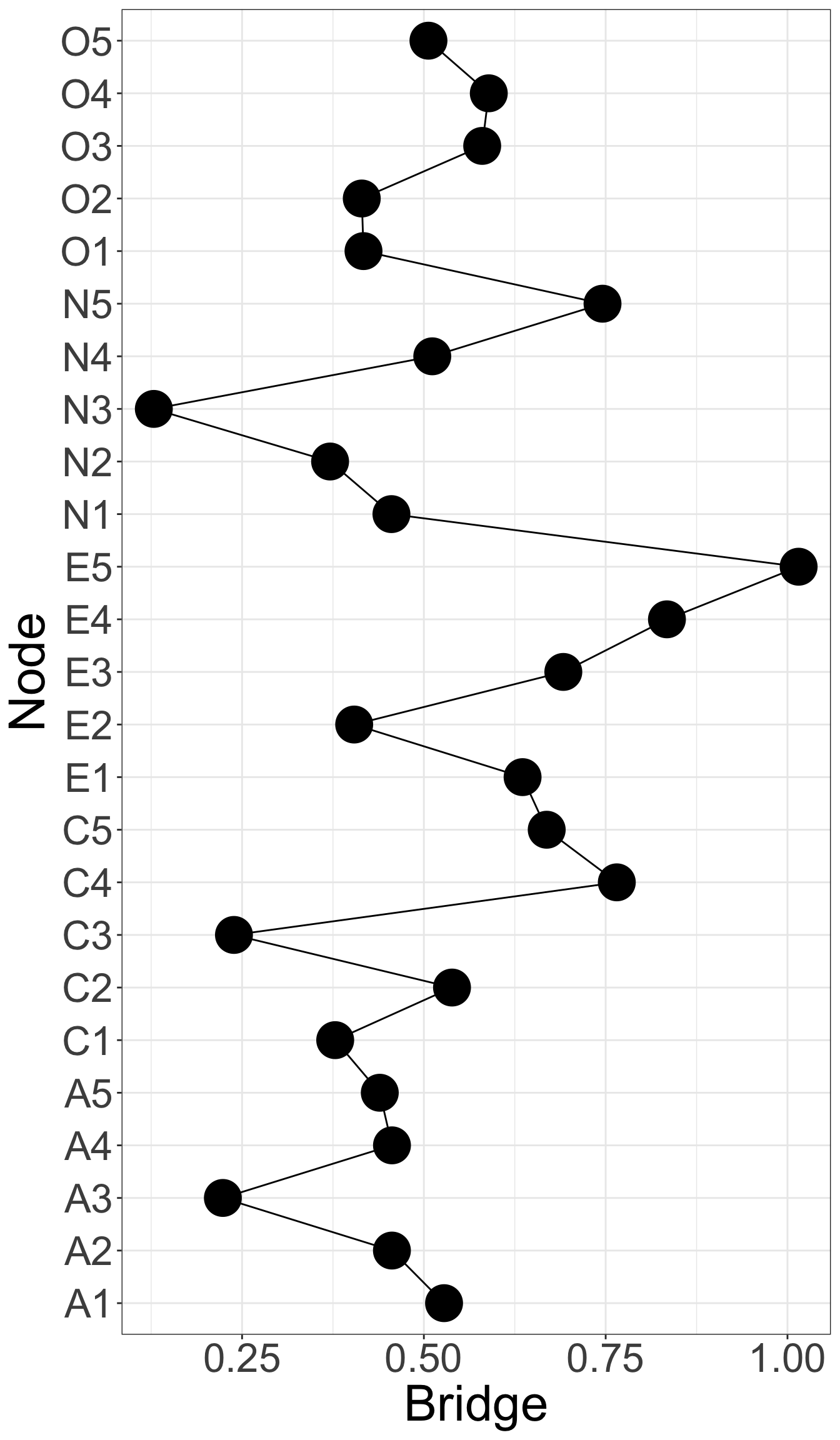
  X1 X3 X5 X9 X10 X13 X14 X18 X21 X23
1  4  5  3  2   2   2   2   2   2   2
2  1  1  1  1   1   1   1   1   1   1
3  2  1  1  3   2   2   2   2   2   2

# One-factor CFA Model
CFA_1factor.syntax = "
factor1 =~ X1 + X3 + X5 + X9 + X10 + X13 + X14 + X18 + X21 + X23
"

#for comparison with EFA we are using standardized factors (var = 1; mean = 0)
CFA_1factor.model = cfa(model = CFA_1factor.syntax, data = data02a, estimator = "MLR", std.lv = TRUE)
summary(CFA_1factor.model, fit.measures = TRUE, standardized = TRUE)

lavaan 0.6.17 ended normally after 21 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        20

                                                  Used       Total
  Number of observations                          1333        1336

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               161.846     104.001
  Degrees of freedom                                35          35
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  1.556
    Yuan-Bentler correction (Mplus variant)                       

Model Test Baseline Model:

  Test statistic                              4148.081    2238.585
  Degrees of freedom                                45          45
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.853

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.969       0.969
  Tucker-Lewis Index (TLI)                       0.960       0.960
                                                                  
  Robust Comparative Fit Index (CFI)                         0.974
  Robust Tucker-Lewis Index (TLI)                            0.966

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)             -16575.733  -16575.733
  Scaling correction factor                                  3.031
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)     -16494.810  -16494.810
  Scaling correction factor                                  2.092
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                               33191.466   33191.466
  Bayesian (BIC)                             33295.370   33295.370
  Sample-size adjusted Bayesian (SABIC)      33231.839   33231.839

Root Mean Square Error of Approximation:

  RMSEA                                          0.052       0.038
  90 Percent confidence interval - lower         0.044       0.032
  90 Percent confidence interval - upper         0.060       0.045
  P-value H_0: RMSEA <= 0.050                    0.318       0.997
  P-value H_0: RMSEA >= 0.080                    0.000       0.000
                                                                  
  Robust RMSEA                                               0.048
  90 Percent confidence interval - lower                     0.037
  90 Percent confidence interval - upper                     0.059
  P-value H_0: Robust RMSEA <= 0.050                         0.604
  P-value H_0: Robust RMSEA >= 0.080                         0.000

Standardized Root Mean Square Residual:

  SRMR                                           0.028       0.028

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  factor1 =~                                                            
    X1                0.581    0.039   15.002    0.000    0.581    0.569
    X3                0.451    0.038   11.896    0.000    0.451    0.521
    X5                0.647    0.041   15.684    0.000    0.647    0.670
    X9                0.542    0.034   16.182    0.000    0.542    0.764
    X10               0.598    0.034   17.355    0.000    0.598    0.688
    X13               0.684    0.037   18.334    0.000    0.684    0.715
    X14               0.562    0.038   14.601    0.000    0.562    0.378
    X18               0.547    0.038   14.438    0.000    0.547    0.429
    X21               0.564    0.036   15.774    0.000    0.564    0.680
    X23               0.635    0.033   19.346    0.000    0.635    0.653

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .X1                0.706    0.063   11.130    0.000    0.706    0.677
   .X3                0.546    0.043   12.732    0.000    0.546    0.728
   .X5                0.513    0.047   10.888    0.000    0.513    0.550
   .X9                0.210    0.016   12.932    0.000    0.210    0.417
   .X10               0.399    0.043    9.297    0.000    0.399    0.527
   .X13               0.447    0.047    9.541    0.000    0.447    0.488
   .X14               1.894    0.078   24.226    0.000    1.894    0.857
   .X18               1.326    0.096   13.842    0.000    1.326    0.816
   .X21               0.370    0.036   10.303    0.000    0.370    0.538
   .X23               0.542    0.047   11.570    0.000    0.542    0.573
    factor1           1.000                               1.000    1.000

CFA Example: Two-factor model

#two factor CFA: one item removed from factor 2 and zero covariance between factors

CFA_2factor.syntax = "
factor1 =~ X1 + X3 + X5 + X9 + X10 + X13 + X14 + X18 + X21 + X23
factor2 =~      X3 + X5 + X9 + X10 + X13 + X14 + X18 + X21 + X23

factor1 ~ 0*factor2
"

#for comparison with EFA we are using standardized factors (var = 1; mean = 0)
CFA_2factor.model = cfa(model = CFA_2factor.syntax, data = data02a, estimator = "MLR", std.lv = TRUE)
summary(CFA_2factor.model, fit.measures = TRUE, standardized = TRUE)

lavaan 0.6.17 ended normally after 42 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        29

                                                  Used       Total
  Number of observations                          1333        1336

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                56.704      39.189
  Degrees of freedom                                26          26
  P-value (Chi-square)                           0.000       0.047
  Scaling correction factor                                  1.447
    Yuan-Bentler correction (Mplus variant)                       

Model Test Baseline Model:

  Test statistic                              4148.081    2238.585
  Degrees of freedom                                45          45
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.853

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.993       0.994
  Tucker-Lewis Index (TLI)                       0.987       0.990
                                                                  
  Robust Comparative Fit Index (CFI)                         0.995
  Robust Tucker-Lewis Index (TLI)                            0.992

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)             -16523.162  -16523.162
  Scaling correction factor                                  2.671
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)     -16494.810  -16494.810
  Scaling correction factor                                  2.092
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                               33104.324   33104.324
  Bayesian (BIC)                             33254.985   33254.985
  Sample-size adjusted Bayesian (SABIC)      33162.865   33162.865

Root Mean Square Error of Approximation:

  RMSEA                                          0.030       0.020
  90 Percent confidence interval - lower         0.019       0.007
  90 Percent confidence interval - upper         0.040       0.029
  P-value H_0: RMSEA <= 0.050                    0.999       1.000
  P-value H_0: RMSEA >= 0.080                    0.000       0.000
                                                                  
  Robust RMSEA                                               0.023
  90 Percent confidence interval - lower                     0.003
  90 Percent confidence interval - upper                     0.038
  P-value H_0: Robust RMSEA <= 0.050                         0.999
  P-value H_0: Robust RMSEA >= 0.080                         0.000

Standardized Root Mean Square Residual:

  SRMR                                           0.017       0.017

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  factor1 =~                                                            
    X1                0.578    0.039   14.876    0.000    0.578    0.566
    X3                0.452    0.038   11.780    0.000    0.452    0.522
    X5                0.659    0.041   16.022    0.000    0.659    0.682
    X9                0.557    0.032   17.200    0.000    0.557    0.784
    X10               0.613    0.035   17.707    0.000    0.613    0.705
    X13               0.671    0.042   16.164    0.000    0.671    0.702
    X14               0.559    0.039   14.279    0.000    0.559    0.376
    X18               0.524    0.045   11.627    0.000    0.524    0.411
    X21               0.555    0.043   13.021    0.000    0.555    0.669
    X23               0.621    0.034   18.196    0.000    0.621    0.639
  factor2 =~                                                            
    X3               -0.023    0.049   -0.466    0.641   -0.023   -0.027
    X5               -0.098    0.069   -1.424    0.154   -0.098   -0.101
    X9               -0.076    0.069   -1.093    0.274   -0.076   -0.107
    X10              -0.108    0.075   -1.430    0.153   -0.108   -0.124
    X13               0.218    0.072    3.034    0.002    0.218    0.228
    X14              -0.011    0.082   -0.140    0.888   -0.011   -0.008
    X18               0.306    0.073    4.205    0.000    0.306    0.240
    X21               0.297    0.089    3.344    0.001    0.297    0.358
    X23               0.161    0.069    2.322    0.020    0.161    0.166

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  factor1 ~                                                             
    factor2           0.000                               0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .X1                0.709    0.065   10.958    0.000    0.709    0.680
   .X3                0.545    0.043   12.668    0.000    0.545    0.727
   .X5                0.489    0.053    9.306    0.000    0.489    0.525
   .X9                0.189    0.020    9.463    0.000    0.189    0.375
   .X10               0.369    0.043    8.665    0.000    0.369    0.488
   .X13               0.417    0.048    8.621    0.000    0.417    0.456
   .X14               1.896    0.078   24.415    0.000    1.896    0.858
   .X18               1.258    0.101   12.423    0.000    1.258    0.774
   .X21               0.291    0.041    7.040    0.000    0.291    0.424
   .X23               0.534    0.051   10.465    0.000    0.534    0.564
   .factor1           1.000                               1.000    1.000
    factor2           1.000                               1.000    1.000

Wrapping up

1. CFA is an alternative model with EFA.

2. The difference is that we have more control over the model structure using CFA, such as we can specify which item(s) loaded on which factors.

3. EFA is not necessary and CFA can be the first step. You just keep revising the model structure until you get acceptable model fitting.

4. Another alternative modeling for dependency among items is network modeling. >>>>>>> a79e7de (local changes)

   • Need to set the right number of constraints for identification
   • We set the value of factor loadings for a few items on a few of the factors
     • Typically to zero
     • Sometimes to one (Brown, 2002)
   • We keep the factor covariance matrix as an identity
     • Uncorrelated factors (as in EFA) with variances of one

<<<<<<< HEAD - Benefits of using CFA for exploratory analyses:

• CFA constraints remove rotational indeterminacy of factor loadings – no rotating is needed (or possible)

  • Defines factors with potentially less ambiguity
  • Constraints are easy to see

• For some software (SAS and SPSS), we get much more model fit information

Example of CFA

See the example from lavaan package

# Background

Network Analysis

a79e7de (local changes)

Network Analysis

Network analysis is a broad area. It has many names in varied fields:

1. Graphical Models (Computer Science, Machine Learning)
2. Bayesian Network (Computer Science, Educational Measurement)
3. Social Network (Sociology)
4. Psychological/Psychometric Network (Psychopathology, Psychology)
5. Structural Equation Model, Path Analysis (Psychology, Education)

1 and 2 focus on the probabilistic relationships and further casual relationships among variables. 3 and 4 focuses on network structure and node importance. 5 focus on the regression coefficients of structural and measurement model.

All 5 analysis methods have a network-shaped diagram. Graphical modeling is a more “general” term that can comprise of the other network models.

Examples of Varied Networks

Figure 1: Bayesian Network (Briganti et al., 2023)

Figure 2: Facebook friendship network in a single undergraduate dorm (Lewis et al., 2008)

Figure 3: Factor Analysis and Psychological Network (Borsboom et al., 2021)

Research Aims

1. Bayesian Network (BN) aims to derive the casual relations between variables
2. Social Network aims to examine the network structure (community, density or centrality) of individuals
3. Factor Analysis aims to identify latent variables
4. Psychological Network aims to examines the associations among observed variables (topological structures) and their positions in the network.

Network Psychometrics

1. Network psychometrics is a novel area that allows representing complex phenomena of measured constructs in terms of a set of elements that interact with each other.
2. It is inspired by the so-called mutualism model and research in ecosystem modeling (Kan, Maas, and Levine 2019).
   • A mutualism model proposes that basic cognitive abilities directly and positively interact during development.
3. Psychometric network arises as dynamics or reciprocal causation among variables are getting more attentions.
4. For example, individual differences in depression could arise from, and could be maintained by, vicious cycles of mutual relationships among symptoms.
5. A depression symptom such as insomnia can cause another symptom, such as fatigue, which in turn can determine concentration problems and worrying, which can result in more insomnia and so on.

Comparison to factor analysis

Factor analysis (common factor model) assumes the associations between observed features can be explained by one or more common factors.

• For example, higher “depression” level leads to increased frequency of depressive behaviors

Psychometric network, however, assumes the associations between observed features ARE the reason of the development of depression. Or “depression” is the network itself.

• unavoidable cycle of “fatigue -> worrying -> insomnia -> fatigue” will leads to higher “depression”

Utility of Psychometric Network

1. Explain the pathways of certain psychological phenomenon
2. Identify the most important problem that needed to be intervene in the treatment procedure
3. Examine group differences in interactions among observed features
4. Examine density of network: more dense network indicates more dynamic of certain problems
5. Examine clusters/communities of observed features: some symptoms are more likely to concur than other symptoms

Terminology I - Overall procedure

1. Network structure estimation: the application of statistical models to assess the structure of pairwise (conditional) associations in multivariate data.
2. Network description: characterization of the global topology and the position of individual nodes in that topology.
3. Psychometric network analysis: the analysis of multivariate psychometric data using network structure estimation and network description.

Terminology II - Network description

1. Node: psychometric variables that are selected in the network
   • such as responses to questionnaire items, symptom ratings, and cognitive test scores, background variables such as age and gender, experimental interventions.
2. Edge (conditional association): associations between variables taking into account other variables that may explain the association
3. Edge weight: parameter estimates that represent the strength of conditional association between nodes
4. Node centrality: the relative importance of a node in the context of other nodes, that can be calculated using different statistics

Terminology III - Network structure estimation

1. Node selection: the choice of which variables will function as nodes in the network model.
2. Network stability analysis: the assessment of estimation precision and robustness to sampling error of psychometric networks.
3. Pairwise Markov random field (PMRF): an undirected network that represents variables as nodes and conditional associations as edges, in which unconnected nodes are conditionally independent.

Exploratory Nature

Psychometric network is exploratory by nature. To obtain a meaningful network structure, psychometric networks need to drop weak edges but keep strong edges.

This procedure is typically called edge selection. One popular edge selection method is regularization.

• Original network structure without regularization is called saturated network; vice versa regularized network

Emotion regulation (Awareness), Interpersonal problems and eating disorder

Workflow of psychometric network

Psychometric network analysis methodology includes steps of network structure estimation (to construct the network), network description (to characterize the network) and network stability analysis (to assess the robustness of results).

Types of data and network models

1. Cross-sectional data (N = large, T = 1)
   • Ising model for categorical variables
   • Gaussian graphical model (GGM; Foygel & Drton, 2010) for continuous variables
   • Mixed graphical model (MGM) for mixed types of variables: include both categorical variables and continuous variables
2. Panel data (N >> T)
   • Multilevel Graphical vector autoregressive model (GVAR)
     • i.e., longitudinal data, repeated measures
3. Time-series data (\(N \geq 1\), T = large)
   • Graphical vector autoregression
     • i.e., ecological momentary assessment, conducted via smartphones

Network Estimation

Gaussian graphical model

GGM is one type of Pairwise Markov random field (PMRF) when data are continuous.

In a PMRF, the joint likelihood of multivariate data is modeled through the use of pairwise conditional associations, leading to a network representation that is undirected.

For \(p\)-dimensional data following multivariate normal distribution:

\[ \boldsymbol{X} \sim \mathcal{N}(\mu, \boldsymbol{K}^{-1}) \]

Where \(K\) is a inverse covariance matrix of \(\boldsymbol{X}\) (\(K = \Sigma^{-1}\)), also known as precision/concentration matrix.

To obtain sparse network structure, the \(i\)th row and \(j\)th column element of \(\boldsymbol{K}\), \(k_{ij}=0\) when edge \(\{j, k\}\) is not included in the network \(G\),

• It means \(X^{(i)}\) and \(X^{(j)}\) are independent conditional on the other variables .

Partial correlation networks

GGM can be standardized as the partial correlation network, in which each edge of GGM representing partial correlations between two nodes.

\[ \rho_{ij}=\rho(X^{(i)}, X^{(j)}|\boldsymbol{X}^{-(i,j)}) = -\frac{k_{ij}}{\sqrt{k_{ii}}\sqrt{k_{jj}}} \]

Assume there are three variables: fatigue, insomnia, concentration

Sigma = matrix(c(
  1,    -.26,  .31,
  -.26,    1, -.08,
  .31,  -.08,    1  
), ncol = 3, byrow = T)
Sigma

      [,1]  [,2]  [,3]
[1,]  1.00 -0.26  0.31
[2,] -0.26  1.00 -0.08
[3,]  0.31 -0.08  1.00

K = solve(Sigma)
round(K, 2)

      [,1] [,2]  [,3]
[1,]  1.18 0.28 -0.34
[2,]  0.28 1.07  0.00
[3,] -0.34 0.00  1.11

R = K
for (i in 1:nrow(R)) {
  for (j in 1:ncol(R)){
    if (i != j) {
      R[i, j] = - K[i, j] / (sqrt(K[i, i])*sqrt(K[j, j]))
    }else{
      R[i, j] = 1
    }
  }
}
round(R, 2)

      [,1]  [,2] [,3]
[1,]  1.00 -0.25  0.3
[2,] -0.25  1.00  0.0
[3,]  0.30  0.00  1.0

Network Interpretation

1. Someone who is tired is also more likely to suffer from concentration problems and insomnia.
2. Concentration problems and insomnia are conditional independent given the level of fatigue
   • Or the correlation between insomnia and concentration can be totally explained by the relationships of both variables with fatigue

qgraph::qgraph(R, labels = c("Fatigue", "Concentration", "Insomnia"))

Estimation of partial correlation model for cross-sectional data

Factor analysis model:

\[ \boldsymbol{X}\sim\mathcal{N}(\mu, \boldsymbol{\Lambda\Psi\Lambda^\text{T}+\Phi}) \]

GGM with partial correlation matrix:

\[ \boldsymbol{X} \sim \mathcal{N}(0, \boldsymbol{\Delta(I-\Omega)^{-1}\Delta}) \]

Where

1. \(\boldsymbol{\Delta}\) is a diagonal scaling matrix that controls the variances
2. \(\boldsymbol{\Omega}\) is a square symmetrical matrix with \(0\)s on the diagonal and partial correlation coefficients on the off diagonal.

psychonetrics: Partial correlation matrix estimation

Sigma |> round(3)

      [,1]  [,2]  [,3]
[1,]  1.00 -0.26  0.31
[2,] -0.26  1.00 -0.08
[3,]  0.31 -0.08  1.00

R |> round(3)

       [,1]   [,2]  [,3]
[1,]  1.000 -0.248 0.300
[2,] -0.248  1.000 0.001
[3,]  0.300  0.001 1.000

library(psychonetrics)
fit = ggm(covs = Sigma, nobs = 50) |> runmodel()
Omega <- fit |> getmatrix("omega") 
Omega |> round(3)# estimated Omega

       [,1]   [,2]  [,3]
[1,]  0.000 -0.248 0.300
[2,] -0.248  0.000 0.001
[3,]  0.300  0.001 0.000

Delta <- fit |> getmatrix(matrix = "delta") 
Delta |> round(3)

      [,1]  [,2]  [,3]
[1,] 0.921 0.000 0.000
[2,] 0.000 0.966 0.000
[3,] 0.000 0.000 0.951

S = Delta %*% solve(diag(1, 3) - Omega) %*% Delta
S |> round(3)

      [,1]  [,2]  [,3]
[1,]  1.00 -0.26  0.31
[2,] -0.26  1.00 -0.08
[3,]  0.31 -0.08  1.00

BGGM: Bayesian approach

library(BGGM)
set.seed(1234)
dat <- mvtnorm::rmvnorm(500, mean = rep(0, 3), sigma = Sigma)
fit_bggm <- BGGM::estimate(dat, type = "continuous", iter = 1000, analytic = FALSE)
fit_bggm$pcor_mat |> round(3)

       [,1]   [,2]  [,3]
[1,]  0.000 -0.258 0.189
[2,] -0.258  0.000 0.040
[3,]  0.189  0.040 0.000

summary(fit_bggm)

BGGM: Bayesian Gaussian Graphical Models 
--- 
Type: continuous 
Analytic: FALSE 
Formula:  
Posterior Samples: 1000 
Observations (n):
Nodes (p): 3 
Relations: 3 
--- 
Call: 
BGGM::estimate(Y = dat, type = "continuous", analytic = FALSE, 
    iter = 1000)
--- 
Estimates:
 Relation Post.mean Post.sd Cred.lb Cred.ub
     1--2    -0.258   0.042  -0.342  -0.173
     1--3     0.189   0.043   0.105   0.274
     2--3     0.040   0.046  -0.055   0.129
--- 

Edge Selection: Regularization

Multiple procedure and software can be used to perform edge selection:

1. prune function in psychonetrics package uses stepdown model search by pruning non-significant parameters

   • a edge with significance level lower than \(\alpha\) will be removed and re-fit the model until no nonsignificant edge existed
   • \(p\) values of edges needed to be adjusted

2. EBICglasso in qgraph and glasso package uses Extended Bayesian Information Criterion (EBIC) to select best model

   \[ \text{EBIC}=-2\text{L}+E(\log(N))+4\gamma E(log(P)) \]

3. select function in BGGM package uses Bayesian Hypothesis Testing — Bayes Factor (BF) to select model

   • \(\mathcal{H}_0: \rho_{ij}=0\)
   • \(\mathcal{H}_1: \rho_{ij}\in(-1, 1)\)
   • \[ BF = \frac{p(\boldsymbol{X}|\mathcal{H}_0)}{p(\boldsymbol{X}|\mathcal{H}_1)} \]
   • By default, edges with BF < 3 will be included

Network Description

1. Network-level metrics:
   • Network stability: The assessment of estimation precision and robustness to sampling error of psychometric networks. Assess whether edge weights and node centrality changes with case dropping subset bootstrap.
   • Network sensitivity: The sensitivity analysis of the network by adding covariates (age, gender, hukou, education, marital status, and self-rated health) to the model to control their confounding effects. Report whether some central nodes are no longer central after adding some variables.
2. Node-level metrics:
   • Total number of node
   • Node centrality: the position of individual nodes within the network. A generic term that subsumes a family of measures that aim to assess how central a node is in a network topology, such as node strength, betweenness and closeness.
   • Node bridge strength: the degree to which one node connects two nodes from different facets. The bridge nodes (nodes with high bridge strength) that connect different communities of nodes (e.g., Neurotic factors is bridge nodes between personality traits and depressive symptoms Li and Zhang (2024)).
   • Node centrality differences between groups: node A is central in group 1’s network but not so central in group 2’s network.
3. Edge-level metrics:
   • Total Number of edges: proportions of non-zero edges
   • Edge weight: edge weights typically are parameter estimates that represent the strength of the conditional association between nodes. Average edge weight can be used to assess the overall strength of network connections.

Example: Big Five Personality Scale

Data Information

25 self-reported personality items representing 5 factors.

70.6% edges are nonzero using EBICglasso, while only 63.6% edges are nonzero using BF method and 62.0% edges are kept using \(\alpha =.01\) significance testing

library(psych)
library(qgraph)
data(bfi)
big5groups <- list(
  Agreeableness = 1:5,
  Conscientiousness = 6:10,
  Extraversion = 11:15,
  Neuroticism = 16:20,
  Openness = 21:25
)
CorMat <- cor_auto(bfi[,1:25])

EBICgraph <- EBICglasso(CorMat, nrow(bfi), 0.5, threshold = TRUE)

## density
density_nonzero_edge <- function(pcor_matrix){
  N_nonzero_edge = (sum(pcor_matrix == 0) - ncol(pcor_matrix)) /2
  N_all_edge = ncol(pcor_matrix)*(ncol(pcor_matrix)-1)/2
  N_nonzero_edge/N_all_edge
}
density_nonzero_edge(EBICgraph)

[1] 0.7066667

PruneFit <- ggm(bfi[,1:25]) |> prune(alpha = .01)
density_nonzero_edge(getmatrix(PruneFit, "omega"))

[1] 0.62

BGGMfit <- BGGM::explore(bfi[,1:25], type = "continuous", iter = 1000, analytic = FALSE) |> 
  select()
density_nonzero_edge(BGGMfit$pcor_mat_zero)

[1] 0.62

Network Structure

EBICglasso

Sig. Test

BF

Centrality - Strength

Strength centrality measures suggest that C4 and E4 or N1 have highest centrality indicating they play most imporatant roles in the networks.

Method 1: EBICglasso

Method 2: Sig. Test

Method 3: Bayes Factor

Centrality - Bridge

E4 and E5 has highest bridge strength, indicating they serve as bridges linking communities of personality. They are important elements connecting varied types of personality

Method 1: EBICglasso

Method 2: Sig. Test

Method 3: Bayes Factor

Wrapping up

1. Network analysis is an alternative way of modeling dependency among variables.
2. Gaussian graphical model is used for multivariate continuous data.
3. The goal is to estimate network structure, node importance, and stability.

Other Materials:

1. Jihong’s post: how to choose network analysis estimation

Reference

Kan, Kees-Jan, Han L. J. van der Maas, and Stephen Z. Levine. 2019. “Extending Psychometric Network Analysis: Empirical Evidence Against g in Favor of Mutualism?” Intelligence 73 (March): 52–62. https://doi.org/10.1016/j.intell.2018.12.004.

Li, Jia, and Jihong Zhang. 2024. “Personality Traits and Depressive Symptoms Among Chinese Older People: A Network Approach.” Journal of Affective Disorders 351 (April): 74–81. https://doi.org/10.1016/j.jad.2024.01.215.