Generalized Measurement Models: Modeling Observed Polytomous Data
Jihong Zhang
Educational Statistics and Research Methods
Previous Class
Dive deep into factor scoring
Show how different initial values affect Bayesian model estimation
Show how parameterization differs for standardized latent variables vs. marker item scale identification
Today’s Lecture Objectives
Show how to estimate unidimensional latent variable models with polytomous data
Also know as Polytomous Item response theory (IRT) or Item factor analysis (IFA)
Distributions appropriate for polytomous (discrete; data with lower/upper limits)
Example Data: Conspiracy Theories
Today’s example is from a bootstrap resample of 177 undergraduate students at a large state university in the Midwest.
The survey was a measure of 10 questions about their beliefs in various conspiracy theories that were being passed around the internet in the early 2010s
All item responses were on a 5-point Likert scale with:
Strong Disagree \(\rightarrow\) 0
Disagree \(\rightarrow\) 0
Neither Agree nor Disagree \(\rightarrow\) 0
Agree \(\rightarrow\) 1
Strongly Agree \(\rightarrow\) 1
The purpose of this survey was to study individual beliefs regarding conspiracies.
Our purpose in using this instrument is to provide a context that we all may find relevant as many of these conspiracies are still prevalent.
From Previous Lectures: CFA (Normal Outcomes)
For comparisons today, we will be using the model where we assumed each outcome was (conditionally) normally distributed:
Recall that this assumption wasn’t good one as the type of data (discrete, bounded, some multimodality) did not match the normal distribution assumption.
Polytomous Data Characteristics
As we have done with each observed variable, we must decide which distribution to use
To do this, we need to map the characteristics of our data on to distributions that share those characteristics
Our observed data:
Discrete responses
Small set of known categories: 1,2,3,4,5
Some observed item responses may be multimodal
Discrete Data Distributions
Stan has a list of distributions for bounded discrete data
Binomial distribution
Pro: Easy to use / code
Con: Unimodal distribution
Beta-binomial distribution
Not often used in psychometrics (but could be)
Generalizes binomial distribution to have different probability for each trial
Hypergeometric distribution
Not often used in psychometrics
Categorical distribution (sometimes called multinomial)
Most frequently used
Base distribution for graded response, partial credit, and nominal response models
Discrete range distribution (sometimes called uniform)
Not useful–doesn’t have much information about latent variables
Binomial Distribution Models
Binomial Distribution Models
The binomial distribution is one of the easiest to use for polytomous items
However, it assumes the distribution of responses are unimodal
n - “number of trials” (range: \(n \in \{0, 1, \dots\}\))
y - “number of successes” out of \(n\) “trials” (range: \(y\in\{0,1,\dots,n\}\))
p - “probability of success” (range: [0, 1])
Mean: \(np\)
Variance: \(np(1-p)\)
Probability Mass Function
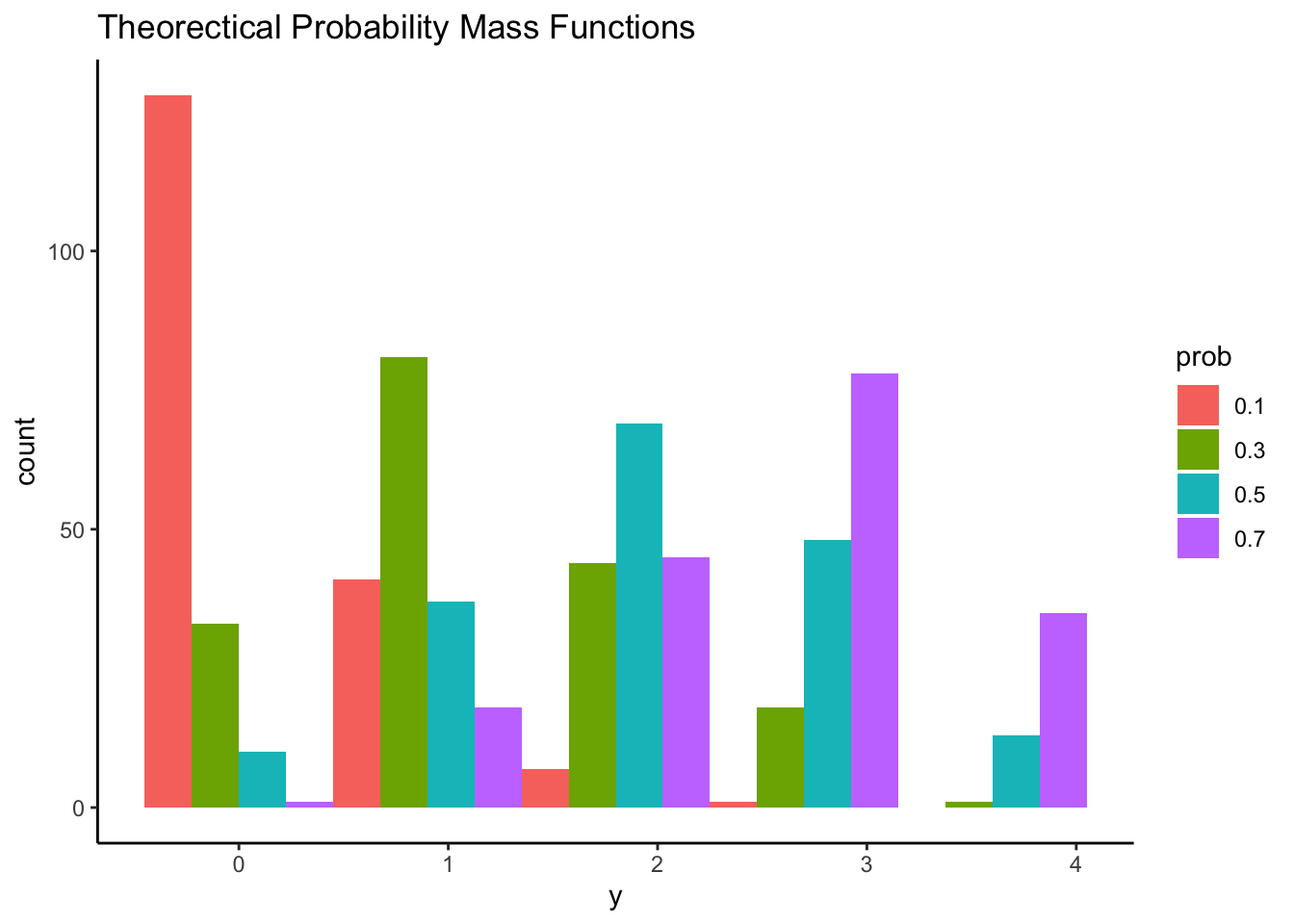
Fixing n = 4 and probability of “brief in conspiracy theory” for each item p = {.1, .3, .5, .7} , we can know probability mass function across each item response from 0 to 4.
Question: which shape of distribution matches our data’s empirical distribution most?
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.0.4
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Attaching package: 'kableExtra'
The following object is masked from 'package:dplyr':
group_rows
here() starts at /Users/jihong/Documents/Projects/website-jihong
Loading required package: Rcpp
This is blavaan 0.5-8
On multicore systems, we suggest use of future::plan("multicore") or
future::plan("multisession") for faster post-MCMC computations.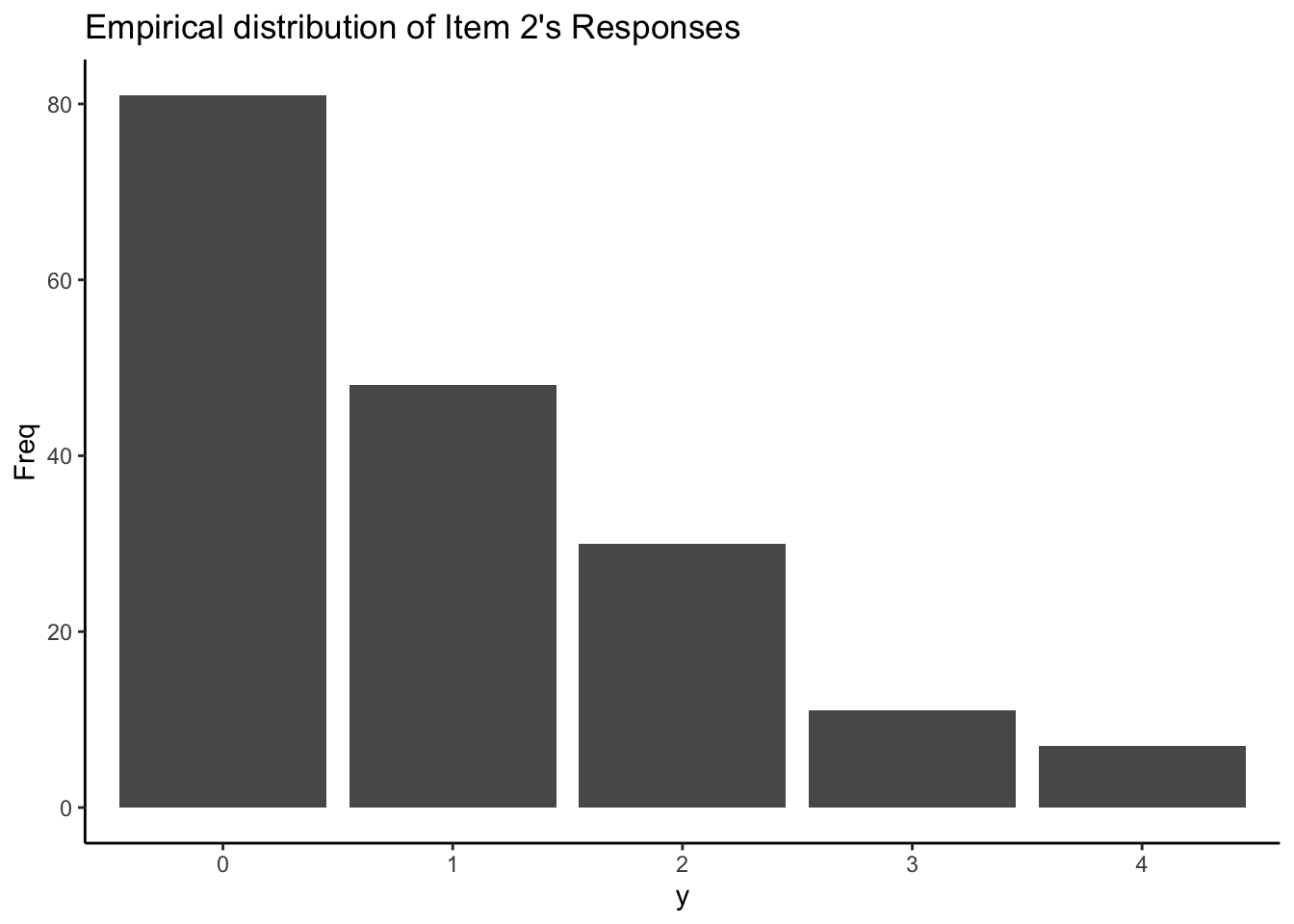
Adapting the Binomial for Item Response Models
Although it doesn’t seem like our items fit with a binomial, we can actually use this distribution
Item response: number of successes \(y_i\)
Needed: recode data so that lowest category is 0 (subtract one from each item)
Highest (recoded) item response: number of trials \(n\)
For all out items, once recoded, \(n_i = 4\)
Then, use a link function to model each item’s \(p_i\) as a function of the latent trait:
Further, we can use the same priors as before on each of our item parameters
\(\mu_i\): Normal Prior \(N(0, 100)\)
\(\lambda_i\): Normal prior \(N(0, 100)\)
Likewise, we can identify the scale of the latent variable as before, too:
\(\theta_p \sim N(0,1)\)
model{} for the Binomial Model in Stan
model { lambda ~ multi_normal(meanLambda, covLambda); // Prior for item discrimination/factor loadings mu ~ multi_normal(meanMu, covMu); // Prior for item intercepts theta ~ normal(0, 1); // Prior for latent variable (with mean/sd specified)for (item in1:nItems){ Y[item] ~ binomial(maxItem[item], inv_logit(mu[item] + lambda[item]*theta)); }}
Here, the binomial item response function has two arguments:
The first part: (maxItem[Item]) is the number of “trials” \(n_i\) (here, our maximum score minus one – 4)
The second part: (inv_logit(mu[item] + lambda[item]*theta)) is the probability from our model (\(p_i\))
The data Y[item] must be:
Type: integer
Range: 0 through maxItem[item]
parameters{} for the Binomial Model in Stan
parameters{vector[nObs] theta; // the latent variables (one for each person)vector[nItems] mu; // the item intercepts (one for each item)vector[nItems] lambda; // the factor loadings/item discriminations (one for each item)}
No changes from any of our previous slope/intercept models
data{} for the Binomial Model in Stan
data {int<lower=0> nObs; // number of observationsint<lower=0> nItems; // number of itemsarray[nItems] int<lower=0> maxItem; // maximum value of Item (should be 4 for 5-point Likert)array[nItems, nObs] int<lower=0> Y; // item responses in an arrayvector[nItems] meanMu; // prior mean vector for intercept parametersmatrix[nItems, nItems] covMu; // prior covariance matrix for intercept parametersvector[nItems] meanLambda; // prior mean vector for discrimination parametersmatrix[nItems, nItems] covLambda; // prior covariance matrix for discrimination parameters}
Note:
Need to supply maxItem (maximum score minus one for each item)
The data are the same (integer) as in the binary/dichotomous item syntax
Preparing Data for Stan
# note: data must start at zeroconspiracyItemsBinomial = conspiracyItemsfor (item in1:ncol(conspiracyItemsBinomial)){ conspiracyItemsBinomial[, item] = conspiracyItemsBinomial[, item] -1}# check first itemtable(conspiracyItemsBinomial[,1])
0 1 2 3 4
49 51 47 23 7
# determine maximum value for each itemmaxItem =apply(X = conspiracyItemsBinomial,MARGIN =2, FUN = max)maxItem
model { lambda ~ multi_normal(meanLambda, covLambda); // Prior for item discrimination/factor loadings theta ~ normal(0, 1); // Prior for latent variable (with mean/sd specified)for (item in1:nItems){ thr[item] ~ multi_normal(meanThr[item], covThr[item]); // Prior for item intercepts Y[item] ~ ordered_logistic(lambda[item]*theta, thr[item]); }}
ordered_logistic is the built-in Stan function for ordered categorical outcomes
Two arguments neeeded for the function
lambda[item]*theta is the muliplications
thr[item] is the thresholds for the item, which is negative values of item intercept
The function expects the response of Y starts from 1
parameters{} for GRM in Stan
parameters {vector[nObs] theta; // the latent variables (one for each person)array[nItems] ordered[maxCategory-1] thr; // the item thresholds (one for each item category minus one)vector[nItems] lambda; // the factor loadings/item discriminations (one for each item)}
Note that we need to declare threshould as: ordered[maxCategory-1] so that
data {int<lower=0> nObs; // number of observationsint<lower=0> nItems; // number of itemsint<lower=0> maxCategory; array[nItems, nObs] int<lower=1, upper=5> Y; // item responses in an arrayarray[nItems] vector[maxCategory-1] meanThr; // prior mean vector for intercept parametersarray[nItems] matrix[maxCategory-1, maxCategory-1] covThr; // prior covariance matrix for intercept parametersvector[nItems] meanLambda; // prior mean vector for discrimination parametersmatrix[nItems, nItems] covLambda; // prior covariance matrix for discrimination parameters}
Note that the input for the prior mean/covariance matrix for threshold parameters is now an array (one mean vector and covariance matrix per item)
Prepare Data for GRM
To match the array for input for the threshold hyperparameter matrices, a little data manipulation is needed
