Lecture 09: Path Analysis

Absolute Model fit and Model Interpretation

Jihong Zhang*, Ph.D

Educational Statistics and Research Methods (ESRM) Program*

University of Arkansas

2024-10-09

Today’s Class

Today's Class

  • Multivariate regression via path model
  • Model modification
  • Comparing and contrasting path analysis
    • Differences in model fit measures
  • How to interpret the results of path model
library(ESRM64503)
library(kableExtra)
library(tidyverse)
library(DescTools) # Desc() allows you to quick screen data
library(lavaan) # Desc() allows you to quick screen data
# options(digits = 3)
head(dataMath)
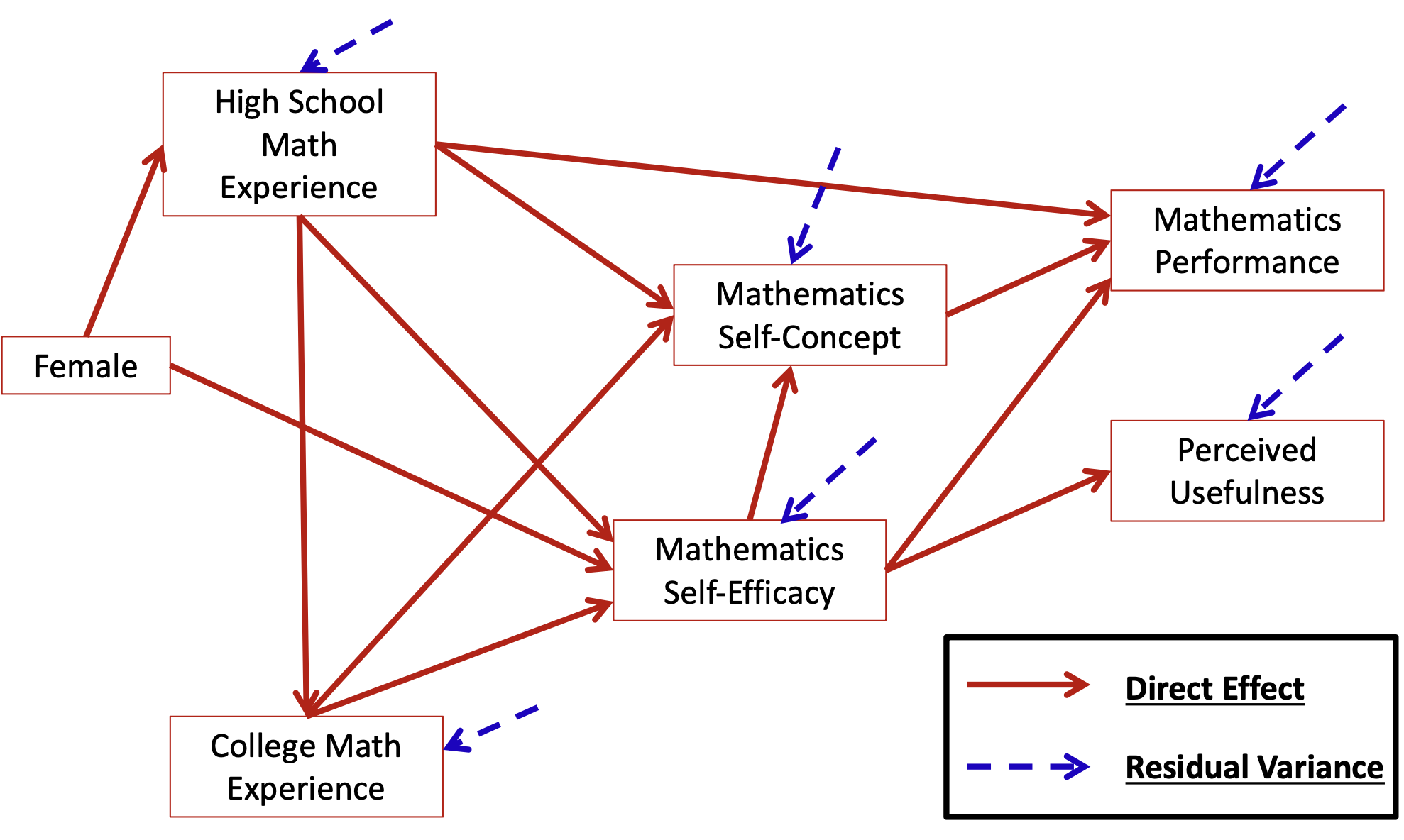
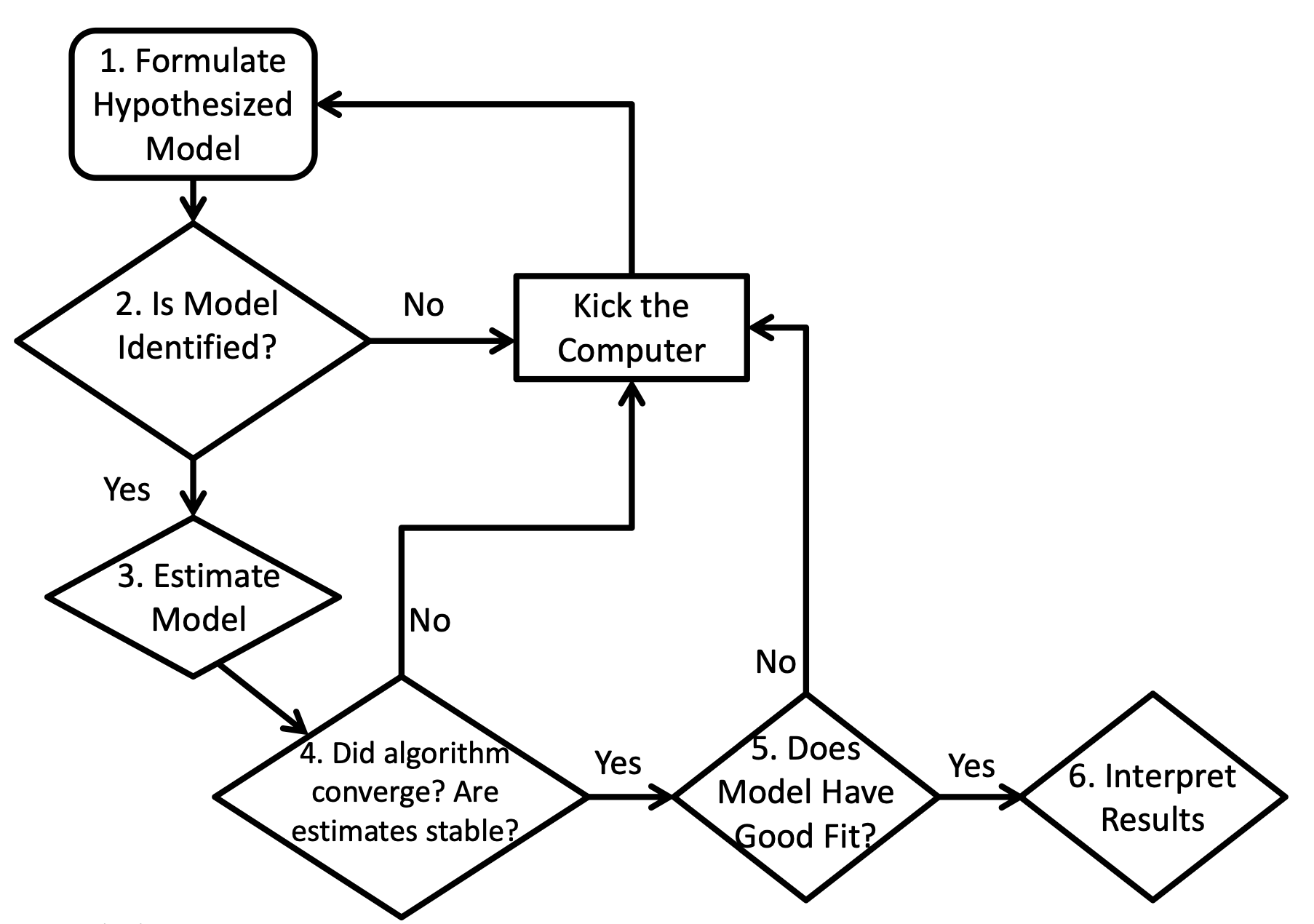
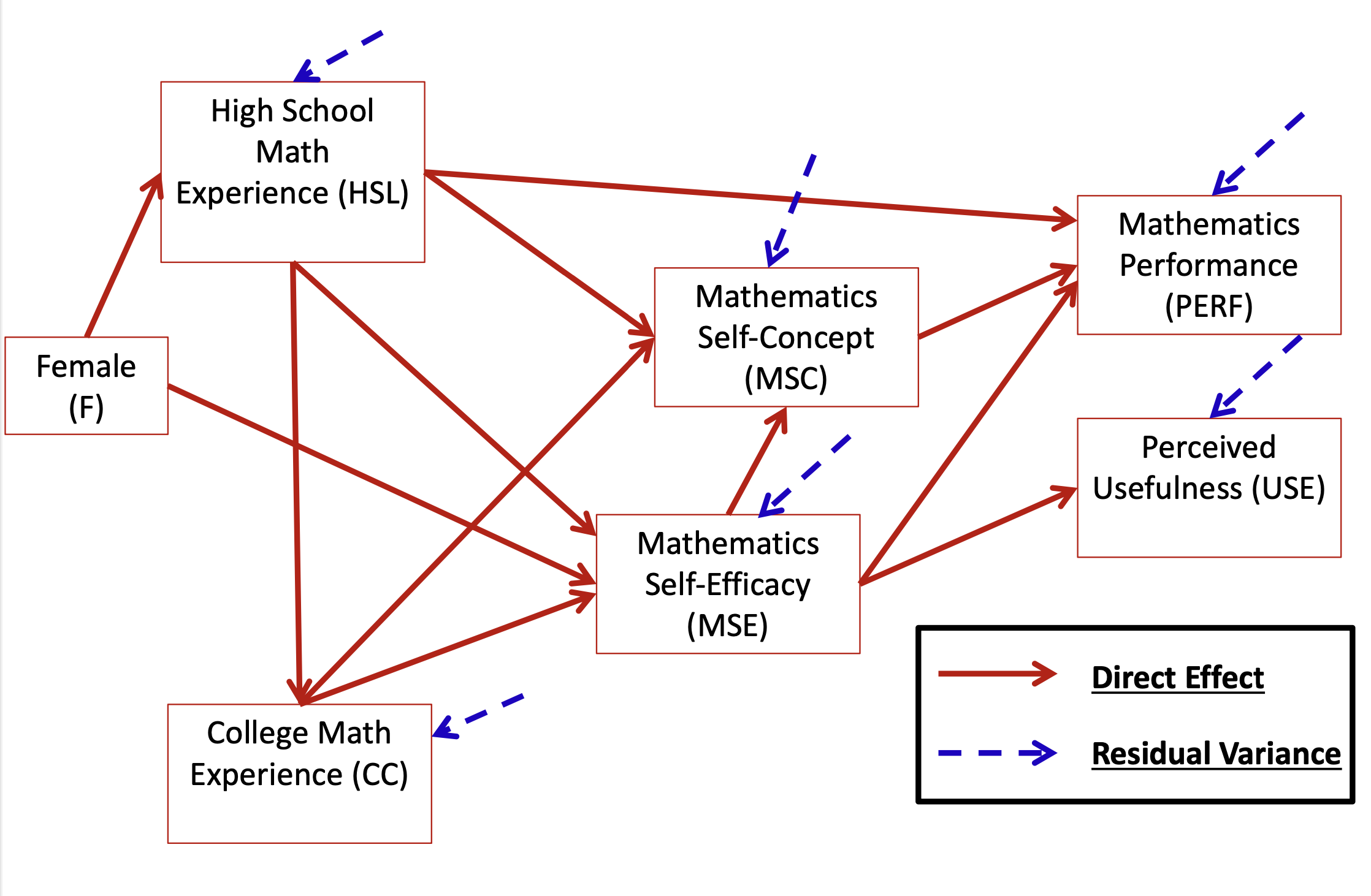
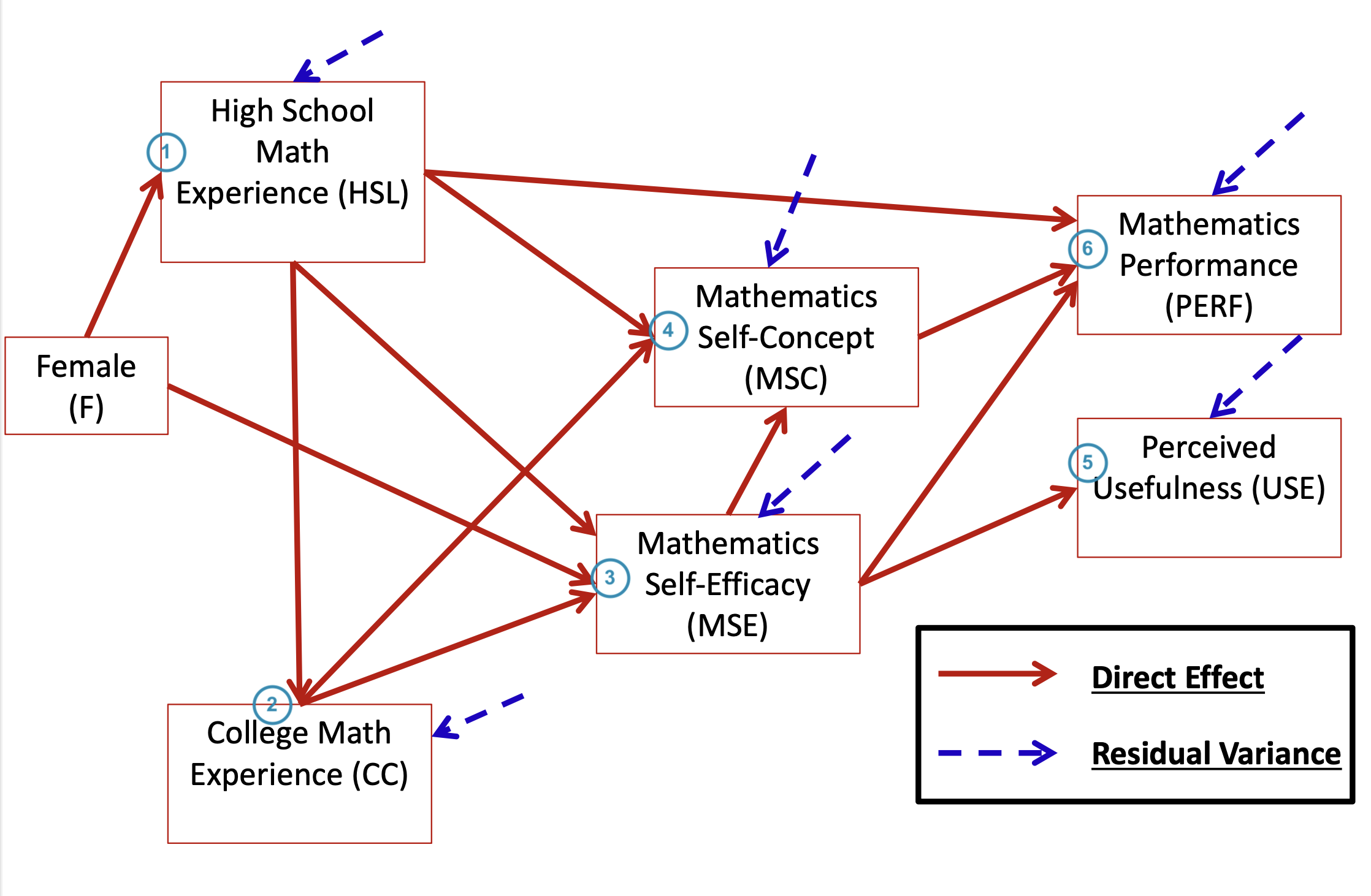
  id hsl cc use msc mas mse perf female
1  1  NA  9  44  55  39  NA   14      1
2  2   3  2  77  70  42  71   12      0
3  3  NA 12  64  52  31  NA   NA      1
4  4   6 20  71  65  39  84   19      0
5  5   2 15  48  19   2  60   12      0
6  6  NA 15  61  62  42  87   18      0
dim(dataMath)
[1] 350   9

Path Analysis

  • Previous models considered simple pairwise correlations among observed variables (perf and use). These models may be limited in answering more complex research questions, such as whether variable A mediates the relationship between variable B and variable C

  • Path analysis is used to analyze multivariate linear models where outcomes can be also predictors

  • Path analysis details:

    • Model identification

    • Modeling workflow

  • Example Analyses

  • Procedure:

    • Model building

    • Model fitting

    • Model summary

Today’s Example Data

  • Data are simulated based on the results reported in:

  • Sample of 350 undergraduates (229 women, 121 men)

    • In simulation, 10% of data points were missing (using missing completely at random mechanism).

Dictionary

  1. Prior Experience at High School Level (HSL)
  2. Prior Experience at College Level (CC)
  3. Perceived Usefulness of Mathematics (USE)
  4. Math Self-Concept (MSC)
  5. Math Anxiety (MAS)
  6. Math Self-Efficacy (MSE)
  7. Math Performance (PERF)
  8. Female (sex variable: 0 = male; 1 = female)

Multivariate Linear Regression Path Diagram

  • This path diagram illustrates a multivariate regression model examining relationships among six constructs related to mathematics education
  • Red solid arrows represent hypothesized direct effects (regression paths) between variables
  • Blue dashed arrows indicate residual variances for endogenous variables
  • The model shows:
    • Female as the sole exogenous variable (predictor with no antecedents)
    • Five endogenous variables: High School Math Experience, College Math Experience, Mathematics Self-Efficacy, Mathematics Self-Concept, Mathematics Performance, and Perceived Usefulness
    • Multiple direct and indirect pathways through which gender and prior experiences influence mathematics outcomes
    • A complex network of relationships suggesting mediation effects through self-beliefs (self-efficacy and self-concept)

The Big Picture

  1. Path analysis is a multivariate statistical method that, when using an identity link, assumes the variables in an analysis are multivariate normally distributed

    • Mean vectors
    • Covariance matrices

  2. By specifying simultaneous regression equations (the core of path models), a very specific covariance matrix is implied

    • This is where things deviate from our familiar R matrix

  3. Like multivariate models, the key to path analysis is finding an approximation to the unstructured (saturated) covariance matrix

    • With fewer parameters, if possible

  4. The art to path analysis is in specifying models that blend theory and statistical evidence to produce valid, generalizable results

Types of Variables in Path Model

  • Endogenous variable(s): variables whose variability is explained by one or more variables in a model
    • In linear regression, the dependent variable is the only endogenous variable in an analysis
      • Mathematics Performance (PERF) and Mathematics Usefulness (USE)
  • Exogenous variable(s): variables whose variability is not explained by any variables in a model
    • In linear regression, the independent variable(s) are the exogenous variables in the analysis
      • Female (F)

Procedure of Path Analysis Steps

Identification of Path Models

  • Model identification is necessary for statistical models to have “meaningful” results

  • For path models, identification can be very difficult

  • Because of their unique structure, path models must have identification in two ways:

    • “Globally” – so that the total number of parameters does not exceed the total number of means, variances, and covariances of the endogenous and exogenous variables

    • “Locally” – so that each individual equation is identified

  • Model identification is guaranteed if a model is both “globally” and “locally” identified

Global Identification: “T-rule”

  • A necessary but not sufficient condition for a path models is that of having equal to or fewer model parameters than there are “distributional parameters”

  • Distributional parameters: As the path models we discuss assume the multivariate normal distribution, we have two matrices of parameters

    • The mean vector
    • The covariance matrix

  • For the MVN, the so-called T-rule states that a model must have equal to or fewer parameters than the unique elements of the covariance matrix of all endogenous and exogenous variables (the sum of all variables in the analysis)

    • Let s=p+q, the total of all endogenous (p) and exogenous (q) variables
    • Then the total unique elements are s(s+1)2

More on the “T-rule”

  • The classical definition of the “T-rule” counts the following entities as model parameters:
    1. Direct effects (regression slopes)
    2. Residual variances
    3. Residual covariances
    4. Exogenous variances
    5. Exogenous covariances
  • Missing from this list are:
    1. The set of exogenous variable means
    2. The set of intercepts for endogenous variables
  • Each of the missing entities are part of the likelihood function, but are considered “saturated” so no additional parameters can be added (all parameters are estimated)
    • These do not enter into the equation for the covariance matrix of the endogenous and exogenous variables

T-rule Identification Status

  • Just-identified: number of observed covariances = number of model parameters
    • Necessary for identification, but no model fit indices available
  • Over-identified: number of observed covariances > number of model parameters
    • Necessary for identification; model fit indices available
  • Under-identified: number of observed covariances < number of model parameters
    • Model is NOT IDENTIFIED: No results available

Our Destination: Overall Path Model

  • Based on the theory described in the introduction to Pajares and Miller (1994), the following model was hypothesized – use this diagram to build your knowledge of path models

Overall Path Model: How to Inspect

Path Model Setup - Questions for the Analysis

  • How many variables are in our model? s=7

    • Gender, HSL, CC, MSC, MSE, PERF, and USE

  • How many variables are endogenous? p=6

    • HSL, CC, MSC, MSE, PERF and USE

  • How many variables are exogenous? q=1

    • Gender

  • Is the model recursive or non-recursive?

    • Recursive – no feedback loops present

Path Model Setup – Questions for the Analysis

  • Is the model identified?

    • Check the t-rule first

    • How many covariance terms are there in the all-variable matrix?

      • 7∗(7+1)2=28

    • How many model parameters are to be estimated?

      • 12 direct paths

      • 6 residual variances (only endogenous variables have resid. var.)

      • 1 variance of the exogenous variable

      • 6 endogenous variance intercepts

        • Not relevant for T-rule identification, but counted in R matrix

  • 28 (total variances/covariances) > (12 + 6 + 1) parameters, thus this model is over-identified

    • We can use R to run analysis

Overall Hypothesized Path Model: Equation Form

  • The path model from can be re-expressed in the following 6 endogenous variable regression equations:

HSLi=β0,HSL+βF,HSLFi+ei,HSL

CCi=β0,CC+βHSL,CCHSLi+ei,CC

MSEi=β0,MSE+βF,MSEFi+βHSL,MSEHSLi+βCC,MSECCi+ei,MSE

MSCi=β0,MSC+βHSL,MSCHSLi+βCC,MSCCCi+βMSE,MSCMSEi+ei,MSC

USEi=β0,USE+βMSE,USEMSEi+ei,USE

PERFi=β0,PERF+βHSL,PERFHSLi+βMSE,PERFMSEi+βMSC,PERFMSCi+ei,PERF

Data Analytic Plan

  1. Model building: Constructed our model

  2. Identification checking (new): Verified it was identified using the t-rule and that it is a recursive model

  3. Model fitting: Estimate the model with R

  4. Model evaluation (new): Check model fit

  5. Model summary: extract results of models

Path Model: lavaan syntax

#model 01-----------------------------------------------------------------------
model01.syntax = 
" 
#endogenous variable equations
perf ~ hsl + msc + mse
use  ~ mse
mse  ~ hsl + cc + female 
msc  ~ mse + cc + hsl
cc   ~ hsl
hsl  ~ female

#endogenous variable intercepts
perf ~ 1
use  ~ 1
mse  ~ 1
msc  ~ 1
cc   ~ 1
hsl  ~ 1

#endogenous variable residual variances
perf ~~ perf
use  ~~ use
mse  ~~ mse
msc  ~~ msc
cc   ~~ cc  
hsl  ~~ hsl

# endogenous variable residual covariances
# this is optional, because by default lavaan will assume their residuals are zero-correlated
# none specfied in the original model so these have zeros:
perf ~~ 0*use + 0*mse + 0*msc + 0*cc + 0*hsl
use  ~~ 0*mse + 0*msc + 0*cc + 0*hsl
mse  ~~ 0*msc + 0*cc + 0*hsl
msc  ~~ 0*cc + 0*hsl
cc   ~~ 0*hsl
"

Model Fit Evaluation

  • First, we check convergence:
    • lavaan’s ML algorithm converged!
#estimate model
model01.fit = sem(model01.syntax, data=dataMath, mimic = "MPLUS", estimator = "MLR")

#see if model converged
inspect(model01.fit, what="converged")
[1] TRUE

  • Second, we check for abnormally large standard errors:

    • None too large, relative to the size of the parameter

    • Indicates identified model

parameterestimates(model01.fit) |> filter(op != "~~")
      lhs op    rhs     est    se      z pvalue ci.lower ci.upper
1    perf  ~    hsl   0.172 0.107  1.600  0.110   -0.039    0.383
2    perf  ~    msc   0.036 0.009  3.981  0.000    0.018    0.054
3    perf  ~    mse   0.139 0.013 10.522  0.000    0.113    0.164
4     use  ~    mse   0.290 0.072  4.014  0.000    0.149    0.432
5     mse  ~    hsl   4.103 0.407 10.085  0.000    3.305    4.900
6     mse  ~     cc   0.393 0.105  3.729  0.000    0.186    0.599
7     mse  ~ female   4.285 1.159  3.697  0.000    2.013    6.557
8     msc  ~    mse   0.721 0.068 10.557  0.000    0.587    0.855
9     msc  ~     cc   0.557 0.132  4.211  0.000    0.298    0.817
10    msc  ~    hsl   2.929 0.659  4.446  0.000    1.638    4.220
11     cc  ~    hsl   0.681 0.246  2.771  0.006    0.199    1.163
12    hsl  ~ female   0.201 0.154  1.307  0.191   -0.101    0.504
13   perf ~1          1.009 0.788  1.281  0.200   -0.535    2.552
14    use ~1         31.118 5.357  5.809  0.000   20.619   41.618
15    mse ~1         47.885 2.246 21.319  0.000   43.482   52.287
16    msc ~1        -23.322 4.542 -5.135  0.000  -32.224  -14.419
17     cc ~1          6.979 1.263  5.524  0.000    4.503    9.455
18    hsl ~1          4.844 0.091 53.434  0.000    4.666    5.021
19 female ~1          0.346 0.000     NA     NA    0.346    0.346
  • Third, we look at the model fit statistics.

Model Fit Statistics

  • Before we interpret the estimation result, we need to assess the fit of a multivariate linear model to the data, in an absolute sense

  • If a model does not fit the data:

    • Parameter estimates may be biased
    • Standard errors of estimates may be biased
    • Inferences made from the model may be wrong
    • If the saturated model fit is wrong, then the LRTs will be inaccurate

  • Not all “good-fitting” models are useful…

    • …model fit just allows you to talk about your model…there may be nothing of significance (statistically or practically) in your results, though

Global measures of Model fit

  1. Root Mean Square Error of Approximation (RMSEA)
  2. Likelihood ratio test
    • User model versus the saturated model: Testing if your model fits as well as the saturated model
    • The saturated model versue the baseline model: Testing whether any variables have non-zero covariances (significant correlations)
  3. User model versus baseline model
    • CFI (the comparative fit index)
    • TLI (the Tucker–Lewis index)
  4. Log-likelihood and Information Criteria
  5. Standardized Root Mean Square Residual (SRMR)
    • How far off a model’s correlations are from the saturated model correlations

Model Fit Statistics: Example

summary(model01.fit, fit.measures = TRUE)
1Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                58.896      58.913
  Degrees of freedom                                 9           9
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  1.000
    Yuan-Bentler correction (Mplus variant)                       

2Model Test Baseline Model:

  Test statistic                               619.926     629.882
  Degrees of freedom                                21          21
  P-value                                        0.000       0.000
  Scaling correction factor                                  0.984

3Root Mean Square Error of Approximation:

  RMSEA                                          0.126       0.126
  90 Percent confidence interval - lower         0.096       0.096
  90 Percent confidence interval - upper         0.157       0.157
  P-value H_0: RMSEA <= 0.050                    0.000       0.000
  P-value H_0: RMSEA >= 0.080                    0.994       0.994  
  
4User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.917       0.918
  Tucker-Lewis Index (TLI)                       0.806       0.809
                                                                  
  Robust Comparative Fit Index (CFI)                         0.918
  Robust Tucker-Lewis Index (TLI)                            0.809

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -5889.496   -5889.496
  Scaling correction factor                                  0.965
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -5860.048   -5860.048
  Scaling correction factor                                  0.975
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                               11826.992   11826.992
  Bayesian (BIC)                             11919.583   11919.583
  Sample-size adjusted Bayesian (SABIC)      11843.446   11843.446
1
This is a likelihood ratio (deviance) test comparing our model (H0) with the saturated model – the saturated model fits much better (χ2(Δdf=9)=58.896, p < .001)
2
This is a likelihood ratio (deviance) test comparing the baseline model with the saturated model
3
The RMSEA estimate is 0.126. Good fit is considered 0.05 or less.
4
The CFI estimate is .917 and the TLI is .806. Good fit is considered 0.95 or higher.
  • Based on the model fit statistics, we conclude that our model does not adequately approximate the covariance matrix. Therefore, inferences from these results may be unreliable due to potentially biased standard errors and parameter estimates

Model Modification Method 1: Check Residual Covariance

  • Having concluded that our model fit is inadequate, we must modify the model to improve fit

    • These modifications are data-driven rather than theory-driven, which raises concerns about their generalizability beyond this sample

  • Ideally, model modifications should be guided by substantive theory

    • However, we can inspect the normalized residual covariance matrix (analogous to z-scores) to identify areas of greatest misfit
    • Several normalized residual covariance exceeds the absolute value of 1.96: MSC with USE and CC with Female
    resid(model01.fit, type = "normalized")$cov
             perf    use    mse    msc     cc    hsl female
perf   -0.076                                          
use    -0.159  0.041                                   
mse    -0.071 -0.110 -0.086                            
msc     0.059  5.051 -0.039  0.043                     
cc     -0.028  0.720 -0.377 -0.161  0.046              
hsl     0.006  0.559  0.085  0.105 -0.034  0.039       
female -1.523 -0.027 -0.425 -1.452 -2.577  0.091  0.000

  • use - msc (5.051) and female - cc (-2.577) have large residuals

sampleCov <- inspect(model01.fit, "sampstat")$cov # covariance matrix from data
modelImpliedCov <- inspect(model01.fit, "cov.ov") # model implied covariance matrix
sampleCov - modelImpliedCov
         perf    use    mse    msc     cc    hsl female
perf   -0.056                                          
use    -0.438  0.792                                   
mse    -0.167 -1.171 -0.908                            
msc     0.202 73.578 -0.517  0.996                     
cc     -0.028  3.894 -1.540 -0.987  0.115              
hsl     0.001  0.622  0.080  0.159 -0.015  0.005       
female -0.120 -0.011 -0.128 -0.666 -0.393  0.003  0.000

Our Destination: Overall Path Model

  • The largest normalized covariances suggest relationships that may be present that are not being modeled:

    • Add a direct effect between Female and CC
    • Add a direct effect (residual covariance) between MSC and USE

Model Modification Method 2: More Help for Fit

  • As we used Maximum Likelihood to estimate our model, another useful feature is that of the modification indices

    • Modification indices (also called Score or LaGrangian Multiplier tests) that attempt to suggest the change in the log-likelihood for adding a given model parameter (larger values indicate a better fit for adding the parameter)
#calculate modification indices
model01.mi = modificationindices(model01.fit, sort. = T)

#display values of indices
head(model01.mi, 10)
      lhs op    rhs     mi    epc sepc.lv sepc.all sepc.nox
54    msc  ~    use 41.517  0.299   0.299    0.275    0.275
31    use ~~    msc 41.517 70.912  70.912    0.386    0.386
46    use  ~    msc 40.032  0.451   0.451    0.490    0.490
63    hsl  ~    mse  6.486  1.139   1.139   10.265   10.265
65    hsl  ~     cc  6.477  0.447   0.447    1.992    1.992
39     cc ~~    hsl  6.477 15.131  15.131    1.974    1.974
59     cc  ~    msc  6.477 -0.568  -0.568   -1.654   -1.654
60     cc  ~ female  6.477 -1.756  -1.756   -0.142   -0.298
70 female  ~     cc  6.477 -0.012  -0.012   -0.145   -0.145
68 female  ~    mse  6.477 -0.030  -0.030   -0.748   -0.748
  • The modification indices have three large values:
    • A direct effect predicting MSC from USE
    • A direct effect predicting USE from MSC
    • A residual covariance between USE and MSC
  • Note: the MI value is -2 times the change in the log-likelihood and the EPC is the expected parameter value
    • The MI is like a 1 DF Chi-Square Deviance test
      • Values greater than 3.84 are likely to be significant changes in the log-likelihood
  • All three modifications involve the same variables; therefore, we can only select one
    • Substantive theory would ideally guide this decision
  • As we do not know theory, we will choose to add a residual covariance between USE and MSC ( the “~~” symbol)
    • This acknowledges that their covariance remains unexplained by the specified model structure—not an ideal theoretical solution, but one that may enable valid inference if adequate model fit is achieved
    • MI = 41.517
    • EPC = 70.912

Model 2: New Model by adding MSE with USE

Model 2: lavaan syntax

#model 02: Add residual covariance between USE and MSC-------------------------------------
model02.syntax = 
" 
#endogenous variable equations
perf ~ hsl + msc + mse
use  ~ mse
mse  ~ hsl + cc + female 
msc  ~ mse + cc + hsl
cc   ~ hsl
hsl  ~ female

#endogenous variable intercepts
perf ~ 1
use  ~ 1
mse  ~ 1
msc  ~ 1
cc   ~ 1
hsl  ~ 1

#endogenous variable residual variances
perf ~~ perf
use  ~~ use
mse  ~~ mse
msc  ~~ msc
cc   ~~ cc  
hsl  ~~ hsl

#endogenous variable residual covariances
#none specfied in the original model so these have zeros:
perf ~~ 0*use + 0*mse + 0*msc + 0*cc + 0*hsl
use  ~~ 0*mse + msc + 0*cc + 0*hsl      #<- the changed part of syntax here (no 0* in front of msc)
mse  ~~ 0*msc + 0*cc + 0*hsl
msc  ~~ 0*cc + 0*hsl
cc   ~~ 0*hsl
"

Assessing Model fit of the Modified Model

#estimate model
model02.fit = sem(model02.syntax, data=dataMath, mimic = "MPLUS", estimator = "MLR")

#see if model converged
inspect(model02.fit, what="converged")
[1] TRUE
#show summary of model fit statistics and parameters
summary(model02.fit, standardized=TRUE, fit.measures=TRUE)
lavaan 0.6-20 ended normally after 80 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        25

  Number of observations                           350
  Number of missing patterns                        26

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                                14.827      14.393
  Degrees of freedom                                 8           8
  P-value (Chi-square)                           0.063       0.072
  Scaling correction factor                                  1.030
    Yuan-Bentler correction (Mplus variant)                       

Model Test Baseline Model:

  Test statistic                               619.926     629.882
  Degrees of freedom                                21          21
  P-value                                        0.000       0.000
  Scaling correction factor                                  0.984

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.989       0.990
  Tucker-Lewis Index (TLI)                       0.970       0.972
                                                                  
  Robust Comparative Fit Index (CFI)                         0.990
  Robust Tucker-Lewis Index (TLI)                            0.973

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -5867.461   -5867.461
  Scaling correction factor                                  0.957
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -5860.048   -5860.048
  Scaling correction factor                                  0.975
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                               11784.923   11784.923
  Bayesian (BIC)                             11881.371   11881.371
  Sample-size adjusted Bayesian (SABIC)      11802.062   11802.062

Root Mean Square Error of Approximation:

  RMSEA                                          0.049       0.048
  90 Percent confidence interval - lower         0.000       0.000
  90 Percent confidence interval - upper         0.088       0.086
  P-value H_0: RMSEA <= 0.050                    0.457       0.484
  P-value H_0: RMSEA >= 0.080                    0.104       0.089
                                                                  
  Robust RMSEA                                               0.053
  90 Percent confidence interval - lower                     0.000
  90 Percent confidence interval - upper                     0.096
  P-value H_0: Robust RMSEA <= 0.050                         0.405
  P-value H_0: Robust RMSEA >= 0.080                         0.170

Standardized Root Mean Square Residual:

  SRMR                                           0.035       0.035

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  perf ~                                                                
    hsl               0.153    0.107    1.432    0.152    0.153    0.068
    msc               0.037    0.009    4.147    0.000    0.037    0.215
    mse               0.139    0.013   10.700    0.000    0.139    0.557
  use ~                                                                 
    mse               0.277    0.073    3.803    0.000    0.277    0.209
  mse ~                                                                 
    hsl               4.138    0.406   10.203    0.000    4.138    0.459
    cc                0.393    0.105    3.723    0.000    0.393    0.194
    female            4.168    1.160    3.593    0.000    4.168    0.166
  msc ~                                                                 
    mse               0.736    0.066   11.119    0.000    0.736    0.512
    cc                0.519    0.117    4.434    0.000    0.519    0.179
    hsl               2.824    0.593    4.764    0.000    2.824    0.218
  cc ~                                                                  
    hsl               0.662    0.247    2.686    0.007    0.662    0.149
  hsl ~                                                                 
    female            0.208    0.154    1.348    0.178    0.208    0.075

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
 .perf ~~                                                               
   .use               0.000                               0.000    0.000
   .mse               0.000                               0.000    0.000
   .msc               0.000                               0.000    0.000
   .cc                0.000                               0.000    0.000
   .hsl               0.000                               0.000    0.000
 .use ~~                                                                
   .mse               0.000                               0.000    0.000
   .msc              70.249   10.358    6.782    0.000   70.249    0.380
   .cc                0.000                               0.000    0.000
   .hsl               0.000                               0.000    0.000
 .mse ~~                                                                
   .msc               0.000                               0.000    0.000
   .cc                0.000                               0.000    0.000
   .hsl               0.000                               0.000    0.000
 .msc ~~                                                                
   .cc                0.000                               0.000    0.000
   .hsl               0.000                               0.000    0.000
 .cc ~~                                                                 
   .hsl               0.000                               0.000    0.000

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .perf              1.023    0.782    1.309    0.191    1.023    0.344
   .use              32.162    5.393    5.964    0.000   32.162    2.035
   .mse              47.738    2.237   21.339    0.000   47.738    4.006
   .msc             -23.369    4.484   -5.211    0.000  -23.369   -1.364
   .cc                7.072    1.268    5.576    0.000    7.072    1.201
   .hsl               4.843    0.091   53.390    0.000    4.843    3.663

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .perf              3.763    0.309   12.173    0.000    3.763    0.427
   .use             238.854   19.097   12.507    0.000  238.854    0.956
   .mse              97.294    7.758   12.541    0.000   97.294    0.685
   .msc             142.912   10.793   13.241    0.000  142.912    0.487
   .cc               33.923    2.456   13.813    0.000   33.923    0.978
   .hsl               1.738    0.126   13.813    0.000    1.738    0.994
needed_fitIndex <- c("rmsea", "srmr","cfi", "tli", "chisq", "df", "pvalue") 
fitmeasures(model02.fit)[needed_fitIndex]
      rmsea        srmr         cfi         tli       chisq          df 
 0.04937683  0.03459811  0.98860192  0.97008004 14.82660076  8.00000000 
     pvalue 
 0.06260610
  • Now we must start over with our path model decision tree
    • The model is identified (now 20 parameters < 28 covariances)
    • Estimation converged; Standard errors look acceptable
  • Model fit indices:
    • The comparison with the saturated model suggests our model fits statistically
    • The RMSEA is 0.049, which indicates good fit
    • The CFI and TLI both indicate good fit (CFI/TLI > .90)
    • The SRMR also indicates good fit
  • Therefore, we conclude the model adequately approximates the covariance matrix, allowing us to proceed with parameter interpretation. However, we first examine the residual covariances and modification indices

Normalized Residual Covariances

resid(model02.fit, type = "normalized")$cov
         perf    use    mse    msc     cc    hsl female
perf   -0.062                                          
use    -0.990  0.020                                   
mse    -0.113  0.064 -0.103                            
msc    -0.003  0.337 -0.104  0.054                     
cc      0.018  0.771 -0.355  0.050  0.034              
hsl     0.062  0.638  0.020  0.154  0.037  0.017       
female -1.500  0.026 -0.362 -1.456 -2.577  0.051  0.000
  • the normalized residual covariance of CC with Female exceeds the absolute value of 1.96
    • Given the number of covariances in the model, this is likely acceptable

Modification Indices for Model 2

model02.mi = modificationindices(model02.fit, sort. = T)
head(model02.mi, 10)
      lhs op    rhs    mi    epc sepc.lv sepc.all sepc.nox
39     cc ~~    hsl 6.697 14.964  14.964    1.949    1.949
68 female  ~    mse 6.697 -0.030  -0.030   -0.761   -0.761
70 female  ~     cc 6.697 -0.012  -0.012   -0.148   -0.148
60     cc  ~ female 6.697 -1.788  -1.788   -0.144   -0.304
58     cc  ~    mse 6.697 -0.429  -0.429   -0.868   -0.868
65    hsl  ~     cc 6.697  0.441   0.441    1.965    1.965
63    hsl  ~    mse 6.696  1.124   1.124   10.128   10.128
66 female  ~   perf 5.126 -0.032  -0.032   -0.199   -0.199
61    hsl  ~   perf 4.410  0.774   0.774    1.739    1.739
69 female  ~    msc 4.405 -0.004  -0.004   -0.162   -0.162

  • No modification indices are substantially large, although some exceed 3.84

    • These are not pursued given that our model demonstrates adequate fit, and adding these parameters may not be theoretically meaningful

More on Modification Indices

  • Recall from our original model that we received the following modification index values for the residual covariance between MSC and USE:
    • MI = 41.529
    • EPC = 70.912
model01.mi[2, ]
   lhs op rhs     mi    epc sepc.lv sepc.all sepc.nox
31 use ~~ msc 41.517 70.912  70.912    0.386    0.386
  • The estimated residual covariance between MSC and USE in the modified model is: 70.249
parameterestimates(model02.fit) |> filter(lhs == "use"& op == "~~"& rhs == "msc")
  lhs op rhs    est     se     z pvalue ci.lower ci.upper
1 use ~~ msc 70.249 10.358 6.782      0   49.947   90.551
  • The difference in log-likelihoods is:
    • -2*(change) = 58.279
anova(model01.fit, model02.fit)

Scaled Chi-Squared Difference Test (method = "satorra.bentler.2001")

lavaan->lavTestLRT():  
   lavaan NOTE: The "Chisq" column contains standard test statistics, not the 
   robust test that should be reported per model. A robust difference test is 
   a function of two standard (not robust) statistics.

            Df   AIC   BIC  Chisq Chisq diff Df diff Pr(>Chisq)    
model02.fit  8 11785 11881 14.827                                  
model01.fit  9 11827 11920 58.896     58.279       1  2.275e-14 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • The values given by the MI and EPC are approximations

Model Parameter Investigation

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  perf ~                                                                
    hsl               0.153    0.107    1.432    0.152    0.153    0.068
    msc               0.037    0.009    4.147    0.000    0.037    0.215
    mse               0.139    0.013   10.700    0.000    0.139    0.557
  use ~                                                                 
    mse               0.277    0.073    3.803    0.000    0.277    0.209
  mse ~                                                                 
    hsl               4.138    0.406   10.203    0.000    4.138    0.459
    cc                0.393    0.105    3.723    0.000    0.393    0.194
    female            4.168    1.160    3.593    0.000    4.168    0.166
  msc ~                                                                 
    mse               0.736    0.066   11.119    0.000    0.736    0.512
    cc                0.519    0.117    4.434    0.000    0.519    0.179
    hsl               2.824    0.593    4.764    0.000    2.824    0.218
  cc ~                                                                  
    hsl               0.662    0.247    2.686    0.007    0.662    0.149
  hsl ~                                                                 
    female            0.208    0.154    1.348    0.178    0.208    0.075

  • Two direct effects are not statistically significant:

    • βF,HSL=.208, p = .178
    • βHSL,PERF=.153, p = .152

  • Although we retain these effects in Model 2, the overall path model suggests they may not be necessary

    • Therefore, we will remove them and re-estimate the model

Model 3: Remove non-significant effects

Model 3: lavaan syntax

#model 03: removing HSL predicting PERF and Gender predicting HSL  ----------------
model03.syntax = 
" 
#endogenous variable equations
perf ~ msc + mse
use  ~ mse
mse  ~ hsl + cc + female 
msc  ~ mse + cc + hsl
cc   ~ hsl

#endogenous variable intercepts
perf ~ 1
use  ~ 1
mse  ~ 1
msc  ~ 1
cc   ~ 1

#endogenous variable residual variances
perf ~~ perf
use  ~~ use
mse  ~~ mse
msc  ~~ msc
cc   ~~ cc  

#endogenous variable residual covariances
#none specfied in the original model so these have zeros:
perf ~~ 0*use + 0*mse + 0*msc + 0*cc 
use  ~~ 0*mse + msc + 0*cc  
mse  ~~ 0*msc + 0*cc 
msc  ~~ 0*cc 
"

#estimate model
model03.fit = sem(model03.syntax, data=dataMath, mimic = "MPLUS", estimator = "MLR")
summary(model03.fit, fit.measures = TRUE)

Model 3: Model fit results

  • We have: an identified model, a converged algorithm, and stable standard errors, so model fit should be inspected
    • Next – inspect model fit
    • Model fit seems to not be as good as we would think
#see if model converged
inspect(model03.fit, what="converged")
[1] TRUE
fitmeasures(model03.fit)[needed_fitIndex]
      rmsea        srmr         cfi         tli       chisq          df 
 0.05739989  0.03674047  0.98265706  0.96146014 18.31095521  9.00000000 
     pvalue 
 0.03173258
  • The largest normalized residual covariance remains that between Female and CC
residuals(model03.fit, type = "normalized")$cov
         perf    use    mse    msc     cc    hsl female
perf   -0.063                                          
use    -1.380  0.025                                   
mse    -0.140  0.129 -0.113                            
msc     0.024  0.303 -0.084  0.065                     
cc     -0.394  0.417 -0.282  0.006  0.017              
hsl     0.949  0.626 -0.055  0.138  0.010  0.000       
female -1.531  0.332 -0.329 -1.886 -2.241  0.000  0.000
  • The modification index for the direct effect of Female on CC is 5.090, indicating that adding this parameter may improve model fit
modificationindices(model03.fit, sort. = T)[1:3,]
    lhs op    rhs    mi    epc sepc.lv sepc.all sepc.nox
36 perf  ~    use 5.625 -0.021  -0.021   -0.111   -0.111
21 perf ~~    use 5.238 -4.264  -4.264   -0.139   -0.139
55   cc  ~ female 5.090 -1.653  -1.653   -0.133   -0.278
  • Accordingly, we will add a direct effect from Female to CC

Model 4: Adding Female on CC

Model 4: lavaan syntax

#model 04: Add gender predicting cc -------------------------------------------------------------
model04.syntax = " 
#endogenous variable equations
perf ~ msc + mse
use  ~ mse
mse  ~ hsl + cc + female 
msc  ~ mse + cc + hsl
cc   ~ hsl + female

#endogenous variable intercepts
perf ~ 1
use  ~ 1
mse  ~ 1
msc  ~ 1
cc   ~ 1

#endogenous variable residual variances
perf ~~ perf
use  ~~ use
mse  ~~ mse
msc  ~~ msc
cc   ~~ cc  

#endogenous variable residual covariances
#none specfied in the original model so these have zeros:
perf ~~ 0*use + 0*mse + 0*msc + 0*cc 
use  ~~ 0*mse + msc + 0*cc  
mse  ~~ 0*msc + 0*cc 
msc  ~~ 0*cc 
"
model04.fit = sem(model04.syntax, data=dataMath, mimic = "MPLUS", estimator = "MLR")

Model 4: Model Fit Index

inspect(model04.fit, what="converged")
[1] TRUE
fitmeasures(model04.fit)[needed_fitIndex]
      rmsea        srmr         cfi         tli       chisq          df 
 0.04531236  0.02405819  0.99039314  0.97598285 13.15766273  8.00000000 
     pvalue 
 0.10653884 
residuals(model04.fit, type = "standardized")$cov
         perf    use    mse    msc     cc    hsl female
perf   -0.065                                          
use    -2.020  0.143                                   
mse    -1.590  1.856 -0.871                            
msc     1.080  1.058  0.835  1.035                     
cc     -0.325  0.498  0.645  0.404 -0.441              
hsl     1.578  0.694 -1.321  0.581  0.286  0.000       
female -1.560  0.433  1.420 -1.500  0.853  0.000  0.000
model04.mi <- modificationindices(model04.fit, sort. = T)
head(model04.mi, 5)
    lhs op    rhs    mi    epc sepc.lv sepc.all sepc.nox
37 perf  ~    use 5.624 -0.021  -0.021   -0.111   -0.111
22 perf ~~    use 5.237 -4.262  -4.262   -0.139   -0.139
41  use  ~   perf 4.860 -1.074  -1.074   -0.201   -0.201
51  msc  ~ female 3.243 -2.626  -2.626   -0.075   -0.156
56  hsl  ~   perf 2.449  0.078   0.078    0.178    0.178

  • We have: an identified model, a converged algorithm, and stable standard errors, so model fit should be inspected

  • No normalized residual covariances exceed the absolute value of 1.96, indicating adequate model fit

  • We will leave this model as-is and interpret the results

Model 4: Parameter Interpretation

  • Interpret each of these parameters as you would in regression:

    • A one-unit increase in HSL brings about a .695 unit increase in CC, holding Female constant

    • std.all: We can also interpret the standardized parameter estimates for all variables except gender

    • A 1-SD increase in HSL means CC increases by 0.153 SD

parameterestimates(model04.fit, standardized = T, ci = F) |> filter(op == "~")
    lhs op    rhs    est    se      z pvalue std.lv std.all std.nox
1  perf  ~    msc  0.042 0.009  4.598  0.000  0.042   0.236   0.236
2  perf  ~    mse  0.151 0.013 11.353  0.000  0.151   0.586   0.586
3   use  ~    mse  0.279 0.079  3.513  0.000  0.279   0.203   0.203
4   mse  ~    hsl  4.050 0.410  9.869  0.000  4.050   0.456   0.347
5   mse  ~     cc  0.383 0.106  3.613  0.000  0.383   0.196   0.196
6   mse  ~ female  3.819 1.201  3.180  0.001  3.819   0.156   0.327
7   msc  ~    mse  0.692 0.070  9.872  0.000  0.692   0.481   0.481
8   msc  ~     cc  0.545 0.120  4.534  0.000  0.545   0.193   0.193
9   msc  ~    hsl  2.894 0.608  4.760  0.000  2.894   0.227   0.172
10   cc  ~    hsl  0.695 0.254  2.737  0.006  0.695   0.153   0.117
11   cc  ~ female -1.662 0.719 -2.312  0.021 -1.662  -0.133  -0.279

Model Interpretation: Explained Variability

sort(inspect(model04.fit, what = 'r2'))
        cc        use        mse        msc       perf 
0.03875216 0.04124687 0.29765620 0.48535191 0.57624994
  • The R2 for each endogenous variable:
    • CC – 0.039
    • USE – 0.041
    • MSE – 0.298
    • MSC – 0.485
    • PERF – 0.576
  • Note that College Experience and Perceived Usefulness both have relatively low proportions of variance explained by the model
    • The R² for Perceived Usefulness could have been increased by specifying a direct path from Math Self-Concept to Perceived Usefulness instead of their residual covariance

Overall Model Interpretation

  • High School Experience and Female are significant predictors of College Experience (βHSL,CC=.695,p=.006 and βF,CC=−1.662,p=.021)

    • Female students report lower College Experience than male students
    • Greater High School Experience is associated with increased College Experience

  • High School Experience, College Experience, and Gender are significant predictors of Math Self-Efficacy (βHSL,MSE=4.05,p<.001; βCC,MSE=.383,p<.001; βF,MSE=3.819,p=.001)

    • Greater High School and College Experience are associated with higher Math Self-Efficacy
    • Female students demonstrate higher Math Self-Efficacy than male students

  • High School Experience, College Experience, and Math Self-Efficacy are significant predictors of Math Self-Concept (βHSL,MSC=2.894,p<.001; βCC,MSC=.545,p<.001; βMSE,MSC=.692,p<.001)

    • Greater High School Experience, College Experience, and Math Self-Efficacy are associated with higher Math Self-Concept

  • Higher Math Self-Efficacy is significantly associated with increased Perceived Usefulness

  • Higher Math Self-Efficacy and Math Self-Concept are associated with improved Math Performance scores

  • Math Self-Concept and Perceived Usefulness exhibit a significant residual covariance

Wrapping Up

  • In this lecture we discussed the basics of path analysis
    • Model specification/identification
    • Model estimation
    • Model fit (necessary, but not sufficient)
    • Model modification and re-estimation
    • Final model parameter interpretation
  • There is a lot to the analysis – but what is important to remember is the over-arching principal of multivariate analyses: covariance between variables is important
    • Path models imply very specific covariance structures
    • The validity of the results hinge upon accurately finding an approximation to the covariance matrix

Next Class

  1. Indirect effect
  2. Causality
  3. Hypothesis tests
  4. Robust ML
Pajares, Frank, and M. David Miller. 1994. “Role of Self-Efficacy and Self-Concept Beliefs in Mathematical Problem Solving: A Path Analysis.” Journal of Educational Psychology 86 (2): 193–203. https://doi.org/10.1037/0022-0663.86.2.193.

ESRM 64503 - Lecture 09: Absolute Model fit and Path Analysis

1 / 43
Lecture 09: Path Analysis Absolute Model fit and Model Interpretation Jihong Zhang*, Ph.D Educational Statistics and Research Methods (ESRM) Program* University of Arkansas 2024-10-09

  1. Slides

  2. Tools

  3. Close
  • Lecture 09: Path Analysis
  • Today’s Class
  • Path Analysis
  • Today’s Example Data
  • Multivariate Linear Regression Path Diagram
  • The Big Picture
  • Types of Variables in Path Model
  • Procedure of Path Analysis Steps
  • Identification of Path Models
  • Global Identification: “T-rule”
  • More on the “T-rule”
  • T-rule Identification Status
  • Our Destination: Overall Path Model
  • Overall Path Model: How to Inspect
  • Path Model Setup - Questions for the Analysis
  • Path Model Setup – Questions for the Analysis
  • Overall Hypothesized Path Model: Equation Form
  • Data Analytic Plan
  • Path Model: lavaan syntax
  • Model Fit Evaluation
  • Model Fit Statistics
  • Global measures of Model fit
  • Model Fit Statistics: Example
  • Model Modification Method 1: Check Residual Covariance
  • Our Destination: Overall Path Model
  • Model Modification Method 2: More Help for Fit
  • Model 2: New Model by adding MSE with USE
  • Model 2: lavaan syntax
  • Assessing Model fit of the Modified Model
  • Normalized Residual Covariances
  • Modification Indices for Model 2
  • More on Modification Indices
  • Model Parameter Investigation
  • Model 3: Remove non-significant effects
  • Model 3: lavaan syntax
  • Model 3: Model fit results
  • Model 4: Adding Female on CC
  • Model 4: lavaan syntax
  • Model 4: Model Fit Index
  • Model 4: Parameter Interpretation
  • Model Interpretation: Explained Variability
  • Overall Model Interpretation
  • Wrapping Up
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • r Scroll View Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help