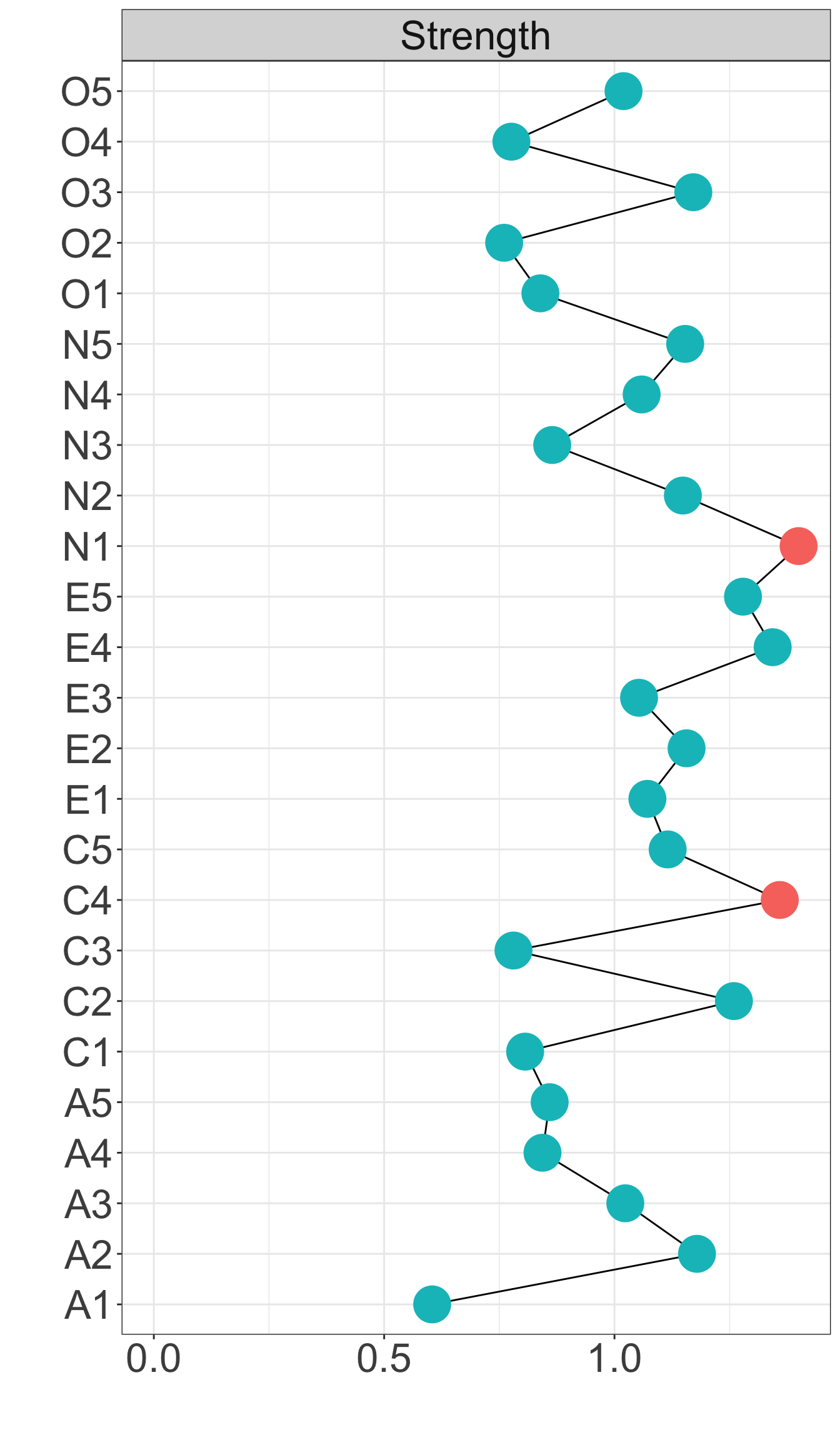
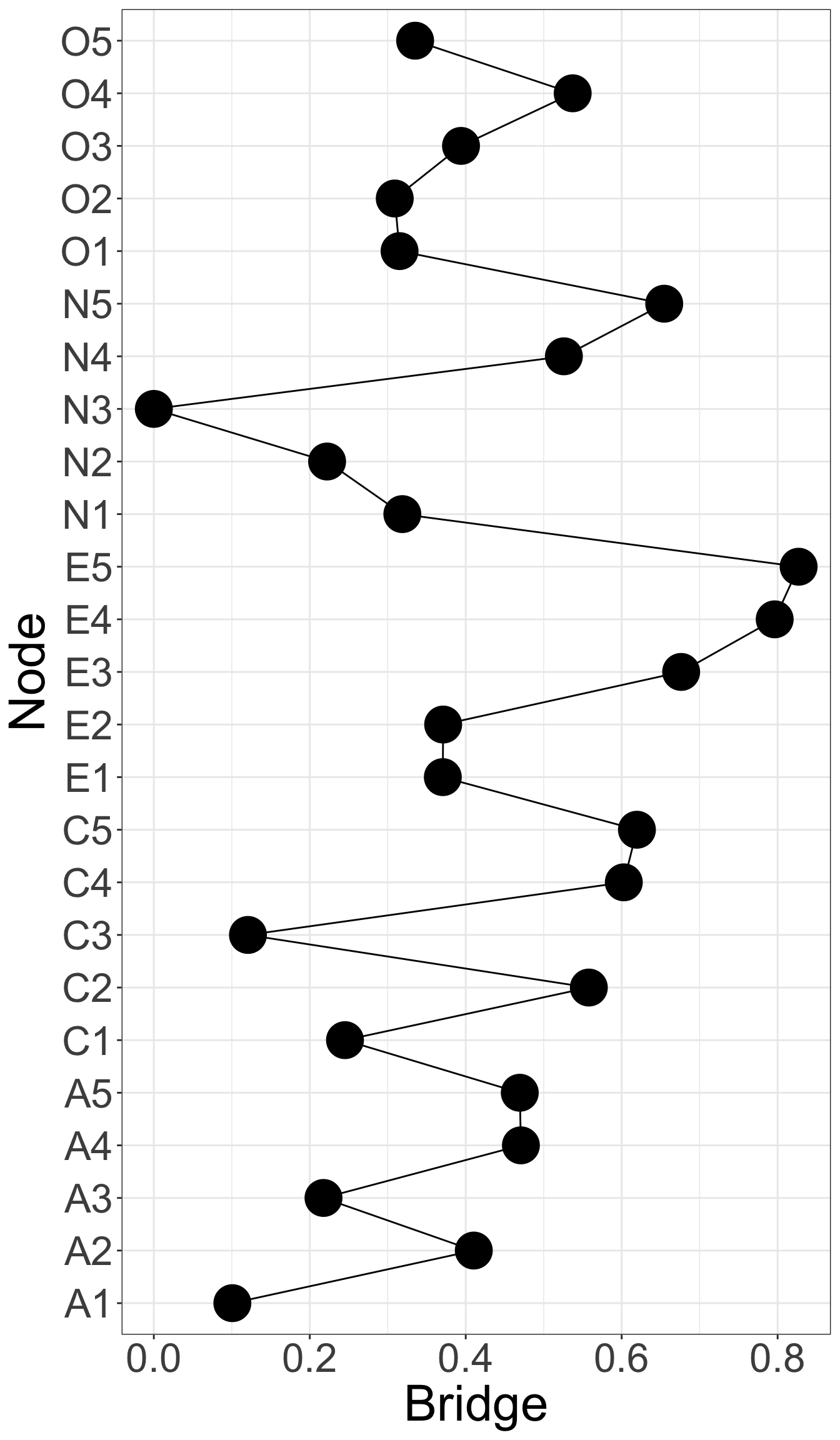
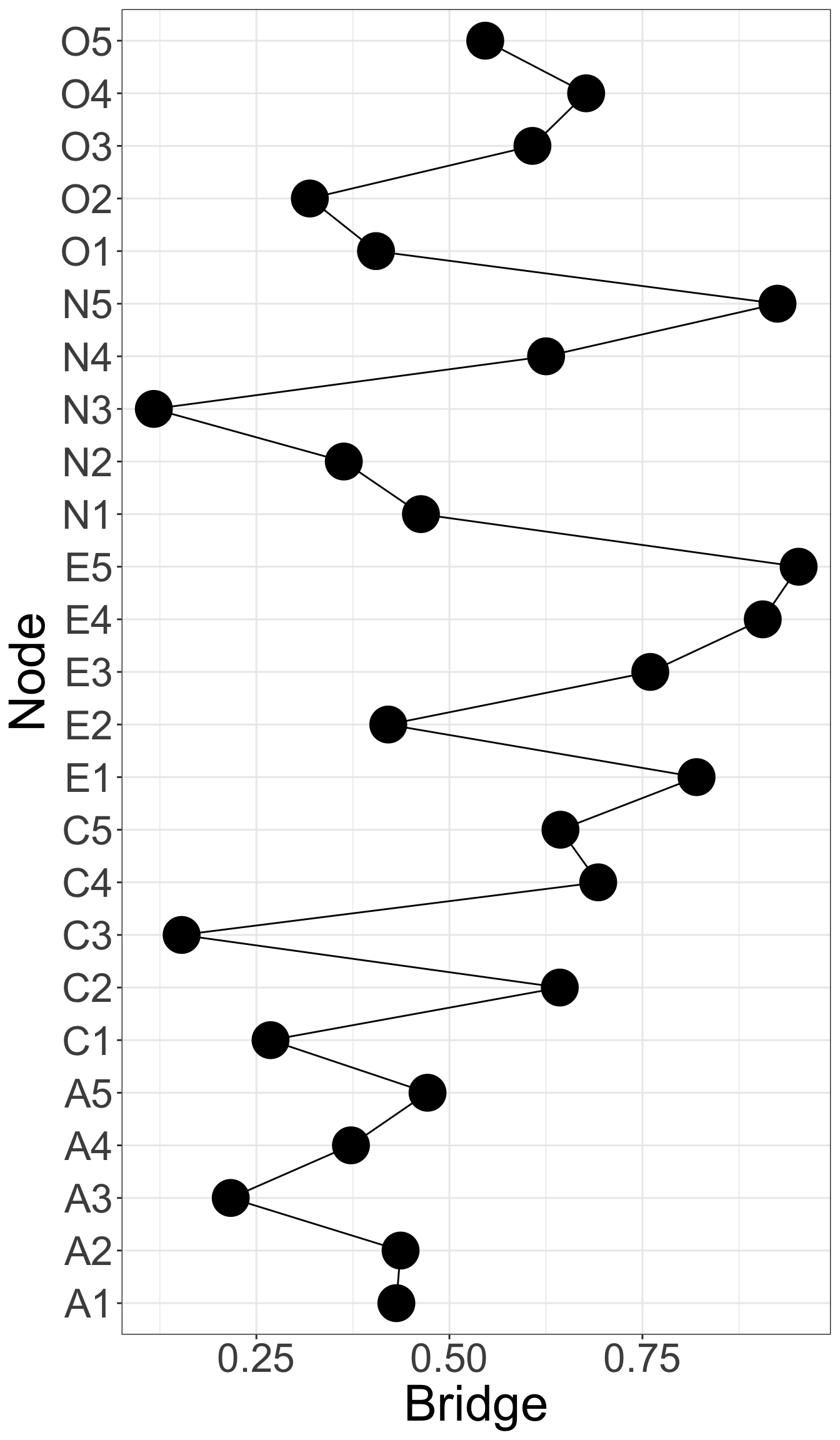
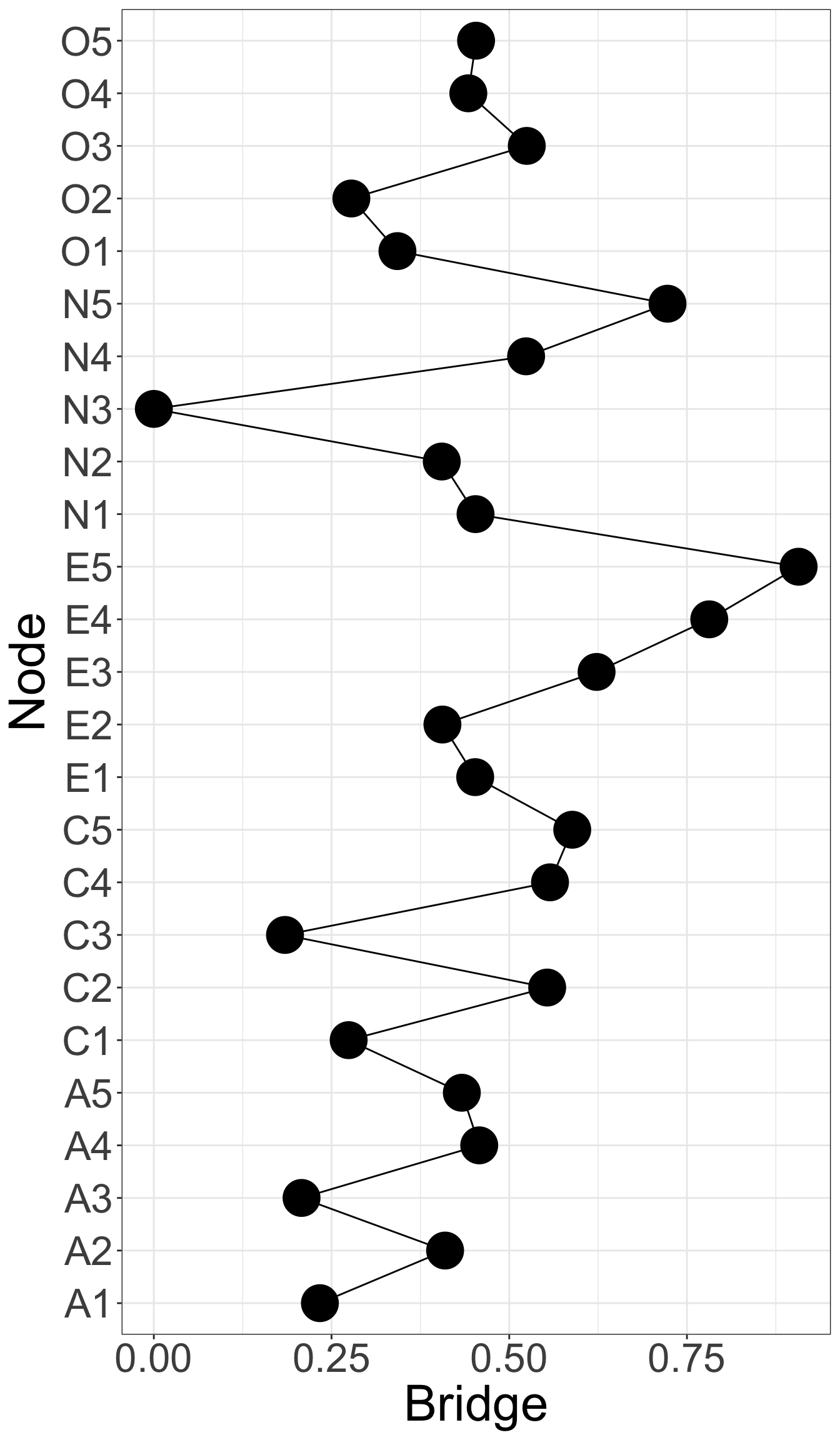
X1 X3 X5 X9 X10 X13 X14 X18 X21 X23
1 4 5 3 2 2 2 2 2 2 2
2 1 1 1 1 1 1 1 1 1 1
3 2 1 1 3 2 2 2 2 2 2# One-factor CFA Model
CFA_1factor.syntax = "
factor1 =~ X1 + X3 + X5 + X9 + X10 + X13 + X14 + X18 + X21 + X23
"
#for comparison with EFA we are using standardized factors (var = 1; mean = 0)
CFA_1factor.model = cfa(model = CFA_1factor.syntax, data = data02a, estimator = "MLR", std.lv = TRUE)
summary(CFA_1factor.model, fit.measures = TRUE, standardized = TRUE)lavaan 0.6-19 ended normally after 21 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 20
Used Total
Number of observations 1333 1336
Model Test User Model:
Standard Scaled
Test Statistic 161.846 104.001
Degrees of freedom 35 35
P-value (Chi-square) 0.000 0.000
Scaling correction factor 1.556
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 4148.081 2238.585
Degrees of freedom 45 45
P-value 0.000 0.000
Scaling correction factor 1.853
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.969 0.969
Tucker-Lewis Index (TLI) 0.960 0.960
Robust Comparative Fit Index (CFI) 0.974
Robust Tucker-Lewis Index (TLI) 0.966
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -16575.733 -16575.733
Scaling correction factor 3.031
for the MLR correction
Loglikelihood unrestricted model (H1) -16494.810 -16494.810
Scaling correction factor 2.092
for the MLR correction
Akaike (AIC) 33191.466 33191.466
Bayesian (BIC) 33295.370 33295.370
Sample-size adjusted Bayesian (SABIC) 33231.839 33231.839
Root Mean Square Error of Approximation:
RMSEA 0.052 0.038
90 Percent confidence interval - lower 0.044 0.032
90 Percent confidence interval - upper 0.060 0.045
P-value H_0: RMSEA <= 0.050 0.318 0.997
P-value H_0: RMSEA >= 0.080 0.000 0.000
Robust RMSEA 0.048
90 Percent confidence interval - lower 0.037
90 Percent confidence interval - upper 0.059
P-value H_0: Robust RMSEA <= 0.050 0.604
P-value H_0: Robust RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.028 0.028
Parameter Estimates:
Standard errors Sandwich
Information bread Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
factor1 =~
X1 0.581 0.039 15.002 0.000 0.581 0.569
X3 0.451 0.038 11.896 0.000 0.451 0.521
X5 0.647 0.041 15.684 0.000 0.647 0.670
X9 0.542 0.034 16.182 0.000 0.542 0.764
X10 0.598 0.034 17.355 0.000 0.598 0.688
X13 0.684 0.037 18.334 0.000 0.684 0.715
X14 0.562 0.038 14.601 0.000 0.562 0.378
X18 0.547 0.038 14.438 0.000 0.547 0.429
X21 0.564 0.036 15.774 0.000 0.564 0.680
X23 0.635 0.033 19.346 0.000 0.635 0.653
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.X1 0.706 0.063 11.130 0.000 0.706 0.677
.X3 0.546 0.043 12.732 0.000 0.546 0.728
.X5 0.513 0.047 10.888 0.000 0.513 0.550
.X9 0.210 0.016 12.932 0.000 0.210 0.417
.X10 0.399 0.043 9.297 0.000 0.399 0.527
.X13 0.447 0.047 9.541 0.000 0.447 0.488
.X14 1.894 0.078 24.226 0.000 1.894 0.857
.X18 1.326 0.096 13.842 0.000 1.326 0.816
.X21 0.370 0.036 10.303 0.000 0.370 0.538
.X23 0.542 0.047 11.570 0.000 0.542 0.573
factor1 1.000 1.000 1.000