Lecture 10: Two-way ANOVA II

Statistics in 2-way ANOVA

Jihong Zhang*, Ph.D

Educational Statistics and Research Methods (ESRM) Program*

University of Arkansas

2025-03-07

Overview of Lecture 09 & Lecture 10

  1. The rest of the semester
  2. Advantage of Factorial Design
  3. Two-way ANOVA:
    • Steps for conducting 2-way ANOVA
    • Hypothesis testing
    • Assumptions for 2-way ANOVA
    • Visualization
    • Difference between 1-way and 2-way ANOVA

Question: How about the research scenario when more than two independent variables?

1 Hypothesis testing for two-way ANOVA

Hypothesis testing for two-way ANOVA (I)

  • For two-way ANOVA, there are three distinct hypothesis tests :
    • Main effect of Factor A
    • Main effect of Factor B
    • Interaction of A and B

Definition

F-test

Three separate F-tests are conducted for each!

Main effect

Occurs when there is a difference between levels for one factor

Interaction

Occurs when the effect of one factor on the DV depends on the particular level of the other factor

Said another way, when the difference in one factor is moderated by the other

Said a third way, if the difference between levels of one factor is different, depending on the other factor

Hypothesis testing for two-way ANOVA (II)

  1. Hypothesis test for the main effect with more than 2 levels

    • Mean differences among levels of one factor:

      1. Differences are tested for statistical significance
      2. Each factor is evaluated independently of the other factor(s) in the study

    • Factor A’s Main effect: “Controlling Factor B, are there differences in the DV across Factor A?”

      \(H_0\): \(\mu_{A_1}=\mu_{A_2}=\cdots=\mu_{A_k}\)

      \(H_1\): At least one \(\mu_{A_i}\) is different from the control group in Factor A

    • Factor B’s Main effect : “Controlling Factor A, are there differences in the DV across Factor B?”

      \(H_0\): \(\mu_{B_1}=\mu_{B_2}=\cdots=\mu_{B_k}\)

      \(H_1\): At least one \(\mu_{B_i}\) is different from the control group in Factor A

    • Interaction effect between A and B:

      \(H_0:\mu_{A_1B_2}-\mu_{A_1B_1}=\mu_{A_2B_2}-\mu_{A_2B_1}\)

      or \(H_0: \mu_{A_1B_1}-\mu_{A_2B_1}=\mu_{A_1B_2}-\mu_{A_2B_2}\)

    The null hypothesis of interaction: B’s group differences do not change across different levels of A. OR A’s group differences do not change at different levels of B.

Hypothesis testing for two-way ANOVA (III)

Example

Background: A researcher is investigating how study method (Factor A: Lecture vs. Interactive) and test format (Factor B: Multiple-Choice vs. Open-Ended) affect student performance (dependent variable: test scores). The study involves randomly assigning students to one of the two study methods and then assessing their performance on one of the two test formats.

  • Main Effect of Study Method (Factor A):
    • H0: There is no difference in test scores between students who used the Lecture method and those who used the Interactive method.
    • H1: There is a significant difference in test scores between the two study methods.
  • Main Effect of Test Format (Factor B):
    • H0: There is no difference in test scores between students taking a Multiple-Choice test and those taking an Open-Ended test.
    • H1: There is a significant difference in test scores between the two test formats.
  • Interaction Effect (Study Method × Test Format):
    • H0: The effect of study method on test scores is the same regardless of test format.
    • H1: The effect of study method on test scores depends on the test format (i.e., there is an interaction).

Hypothesis testing for two-way ANOVA (IV)

Example: Tutoring Program and Types of Schools on Grades

  • IVs:
    1. Tutoring Programs: (1) No tutor; (2) Once a week; (3) Daily
    2. Types of schools: (1) Public (2) Private-secular (3) Private-religious
  • Research purpose: to examine the effect of tutoring program (no tutor, once a week, and daily) AND types of school (e.g., public, private-secular, and private-religious) on the students’ grades
  • Question: What are the null and alternative hypotheses for the main effects in the example?:

    • Factor A’s Main effect: “Controlling school types, are there differences in the students’ grade across three tutoring programs?”

      \(H_0\): \(\mu_{\mathrm{no\ tutor}}=\mu_{\mathrm{once\ a\ week}}=\mu_{\mathrm{daily}}\)

    • Factor B’s Main effect : “Controlling tutoring programs, are there differences in the students’ grades across three school types?”

      \(H_0\): \(\mu_{\mathrm{public}}=\mu_{\mathrm{private-religious}}=\mu_{\mathrm{private-secular}}\)

Model 1: Two-Way ANOVA without interaction

  • The main-effect only ANOVA with no interaction has a following statistical form:

\[ \mathrm{Grade} = \beta_0 + \beta_1 \mathrm{Toturing_{Once}} + \beta_2 \mathrm{Toturing_{Daily}} \\ + \beta_3 \mathrm{SchoolType_{PvtS}} + \beta_4 \mathrm{SchoolType_{PvtR}} \]

Data Generation 
library(tidyverse)
# Set seed for reproducibility
set.seed(123)

# Define sample size per group
n <- 30

# Define factor levels
tutoring <- rep(c("No Tutor", "Once a Week", "Daily"), each = 3 * n)
school <- rep(c("Public", "Private-Secular", "Private-Religious"), times = n * 3)

# Simulate student grades with assumed effects
grades <- c(
  rnorm(n, mean = 75, sd = 5),  # No tutor, Public
  rnorm(n, mean = 78, sd = 5),  # No tutor, Private-Secular
  rnorm(n, mean = 76, sd = 5),  # No tutor, Private-Religious
  rnorm(n, mean = 80, sd = 5),  # Once a week, Public
  rnorm(n, mean = 83, sd = 5),  # Once a week, Private-Secular
  rnorm(n, mean = 81, sd = 5),  # Once a week, Private-Religious
  rnorm(n, mean = 85, sd = 5),  # Daily, Public
  rnorm(n, mean = 88, sd = 5),  # Daily, Private-Secular
  rnorm(n, mean = 86, sd = 5)   # Daily, Private-Religious
)
# Create a dataframe
data <- data.frame(
  Tutoring = factor(tutoring, levels = c("No Tutor", "Once a Week", "Daily")),
  School = factor(school, levels = c("Public", "Private-Secular", "Private-Religious")),
  Grades = grades
)
  • Main effect of Tutoring Programs
    • Collapsing across School Type
    • Ignoring the difference levels of School Type
    • Averaging DV regarding Tutoring Programs across the levels of School Type
  • Main effect of School Type
    • Collapsing across Tutoring Program
    • Ignoring the difference levels of Tutoring Program
    • Averaging DV regarding School Type across the levels of Tutoring Programs

Ignoring the effect of school types, we can tell the main effect of tutor programs on students’ grades (Daily tutoring has the highest grade, followed by once a week).

Code 
# Compute mean and standard error for each tutoring group
tutoring_summary <- data |>
  group_by(Tutoring) |>
  summarise(
    Mean_Grade_byTutor = mean(Grades)
  )

school_summary <- data |>
  group_by(School) |>
  summarise(
    Mean_Grade_bySchool = mean(Grades)
  )

total_summary <- tutoring_summary |>
  cbind(school_summary)

# Plot main effect of tutoring
ggplot(total_summary, aes(x = School)) +
  geom_point(aes(y = Mean_Grade_byTutor, color = Tutoring), size = 5) +
  geom_hline(aes(yintercept = Mean_Grade_byTutor, color = Tutoring), linewidth = 1.3) +
  scale_y_continuous(limits = c(70, 90), breaks = seq(70, 90, 5)) +
  labs(title = "Main Effect of Tutoring on Student Grades",
       x = "School Types",
       y = "Mean Grade") +
  theme_minimal()

distinct(tutoring_summary[, c("Tutoring", "Mean_Grade_byTutor")])
# A tibble: 3 × 2
  Tutoring    Mean_Grade_byTutor
  <fct>                    <dbl>
1 No Tutor                  76.6
2 Once a Week               81.1
3 Daily                     86.3
  • The x-axis represents three school types.
  • The y-axis represents the mean student grades for the different tutoring programs: No Tutor, Once a Week, and Daily.
  • If the main effect of tutoring is significant, we expect to see noticeable differences in mean grades across tutoring conditions.

You turn: Visualize Main Effect of School Type

Combined Visualization for no-interaction model

  • There is the LARGE effect of Factor Tutoring and very small effect of School Type:
    • Effect of Factor Tutoring: the LARGE vertical distance
    • Effect of Factor School Type: the very small horizontal distance

Real-World Examples of Interaction Effects

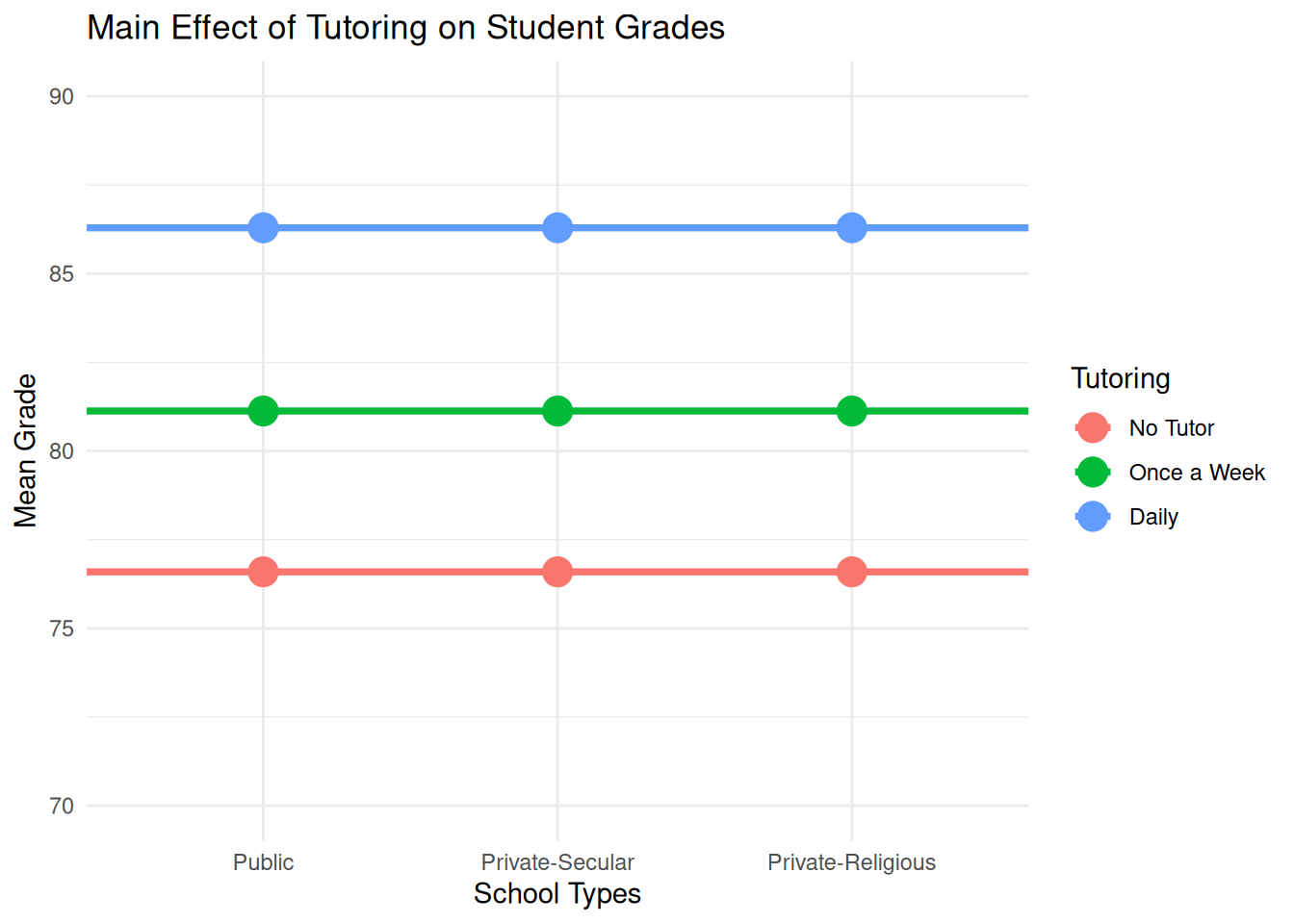
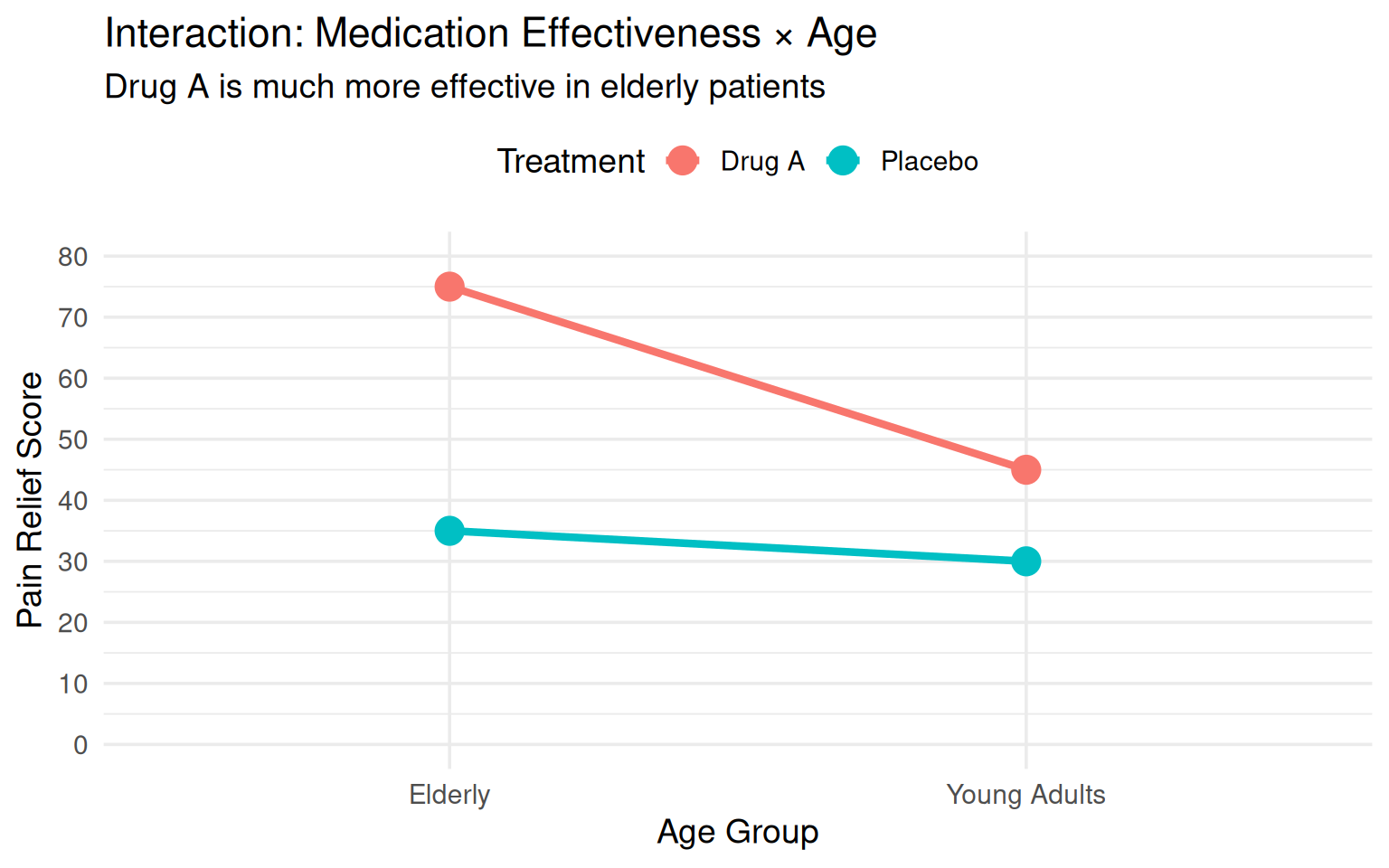
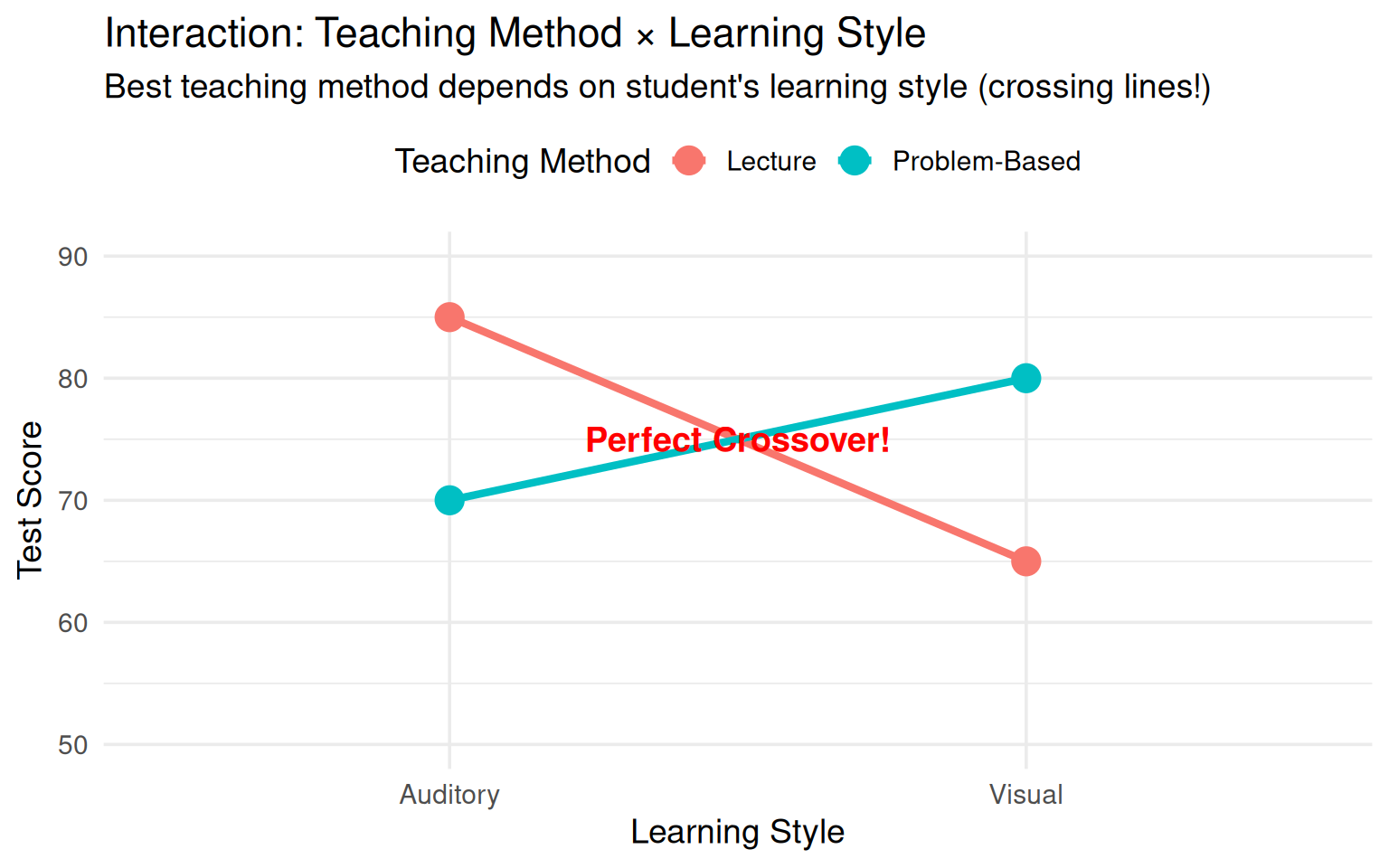
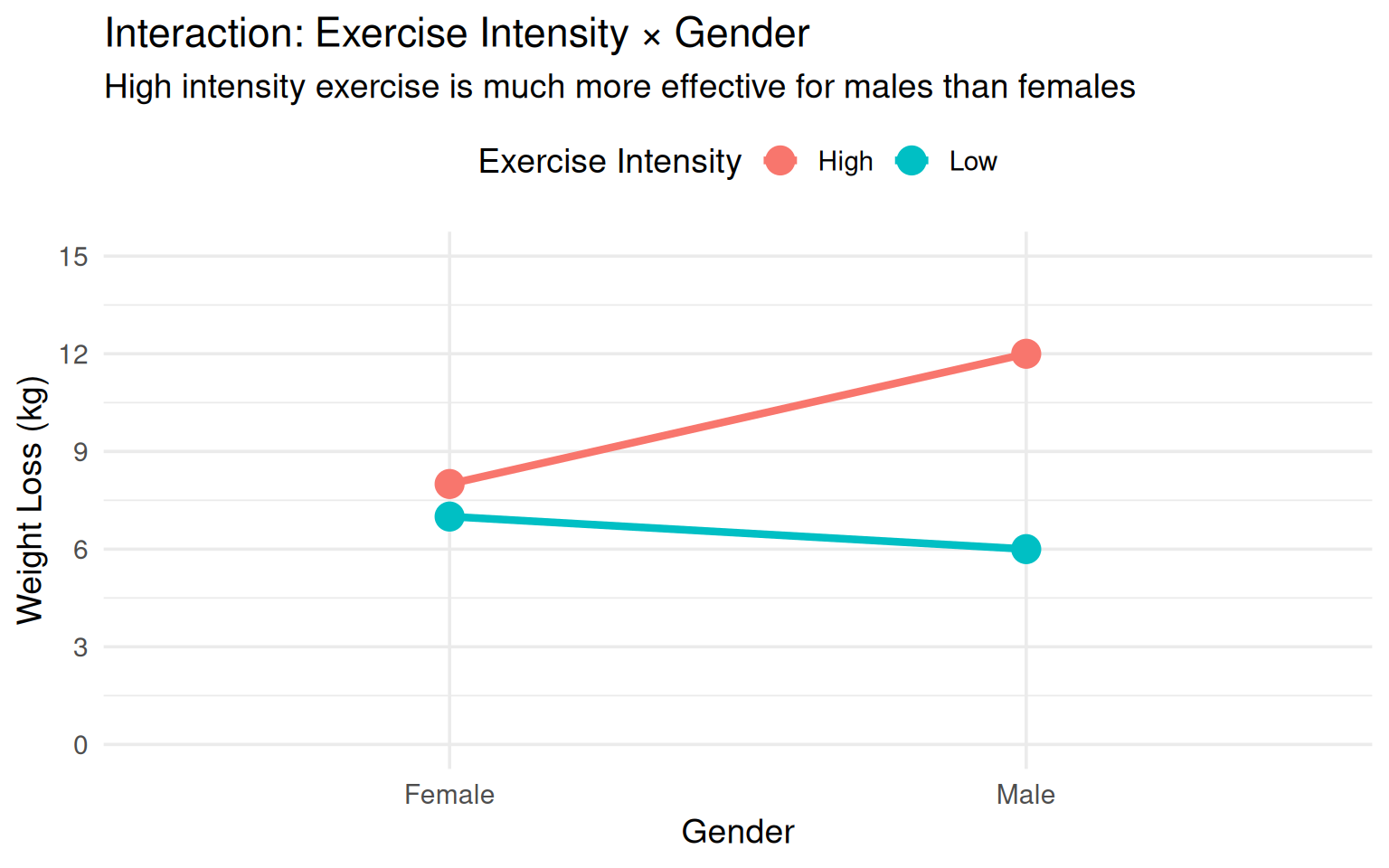
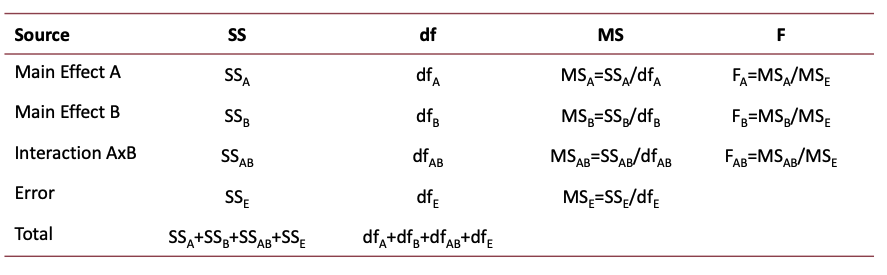
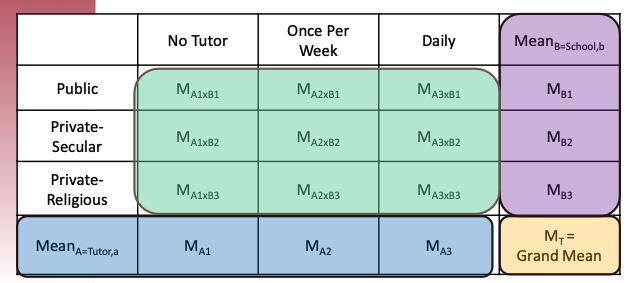
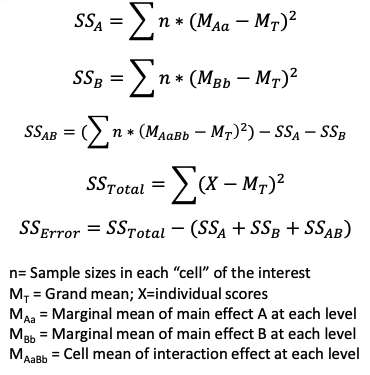
Research Question: Does the effectiveness of a new pain medication depend on patient age?

Factors:

  • Factor A: Medication Type (Drug A vs. Placebo)
  • Factor B: Age Group (Young Adults vs. Elderly)

Observed Pattern (Interaction Present):

  • Young Adults: Drug A shows moderate improvement over placebo (Δ = 15 points)
  • Elderly: Drug A shows LARGE improvement over placebo (Δ = 40 points)

Why the interaction?

  • Elderly patients may have different metabolism rates
  • Age-related changes in pain receptors may make them more responsive to the drug
  • Elderly may have more severe baseline pain, allowing more room for improvement

Implication: You cannot simply say “Drug A works” - you must specify “Drug A works especially well for elderly patients”

Visualization:

Research Question: Does the best teaching method depend on students’ learning style?

Factors:

  • Factor A: Teaching Method (Lecture-Based vs. Problem-Based Learning)
  • Factor B: Learning Style (Visual vs. Auditory Learners)

Observed Pattern (Interaction Present):

  • Visual Learners: Problem-Based Learning >> Lecture-Based (80 vs. 65)
  • Auditory Learners: Lecture-Based >> Problem-Based Learning (85 vs. 70)

Why the interaction?

  • Visual learners benefit from hands-on activities with diagrams and visual aids in PBL
  • Auditory learners benefit from verbal explanations and discussions in lectures
  • One-size-fits-all teaching ignores individual differences in cognitive processing

Implication: Educational policy should consider matching teaching methods to learning styles, not universally adopting one method.

Visualization:

Research Question: Does the effect of exercise intensity on weight loss depend on biological sex?

Factors:

  • Factor A: Exercise Intensity (Low vs. High Intensity)
  • Factor B: Gender (Male vs. Female)

Observed Pattern (Interaction Present):

  • Males: High intensity >> Low intensity (12 kg vs. 6 kg lost)
  • Females: High intensity ≈ Low intensity (8 kg vs. 7 kg lost)

Why the interaction?

  • Males typically have higher muscle mass and testosterone, enabling better response to high-intensity training
  • Females may have hormonal differences affecting metabolism response to exercise intensity
  • High-intensity exercise may increase cortisol more in females, potentially interfering with weight loss
  • Different fat distribution patterns between sexes respond differently to exercise intensity

Implication: Exercise prescriptions should be sex-specific, not generic.

Visualization:

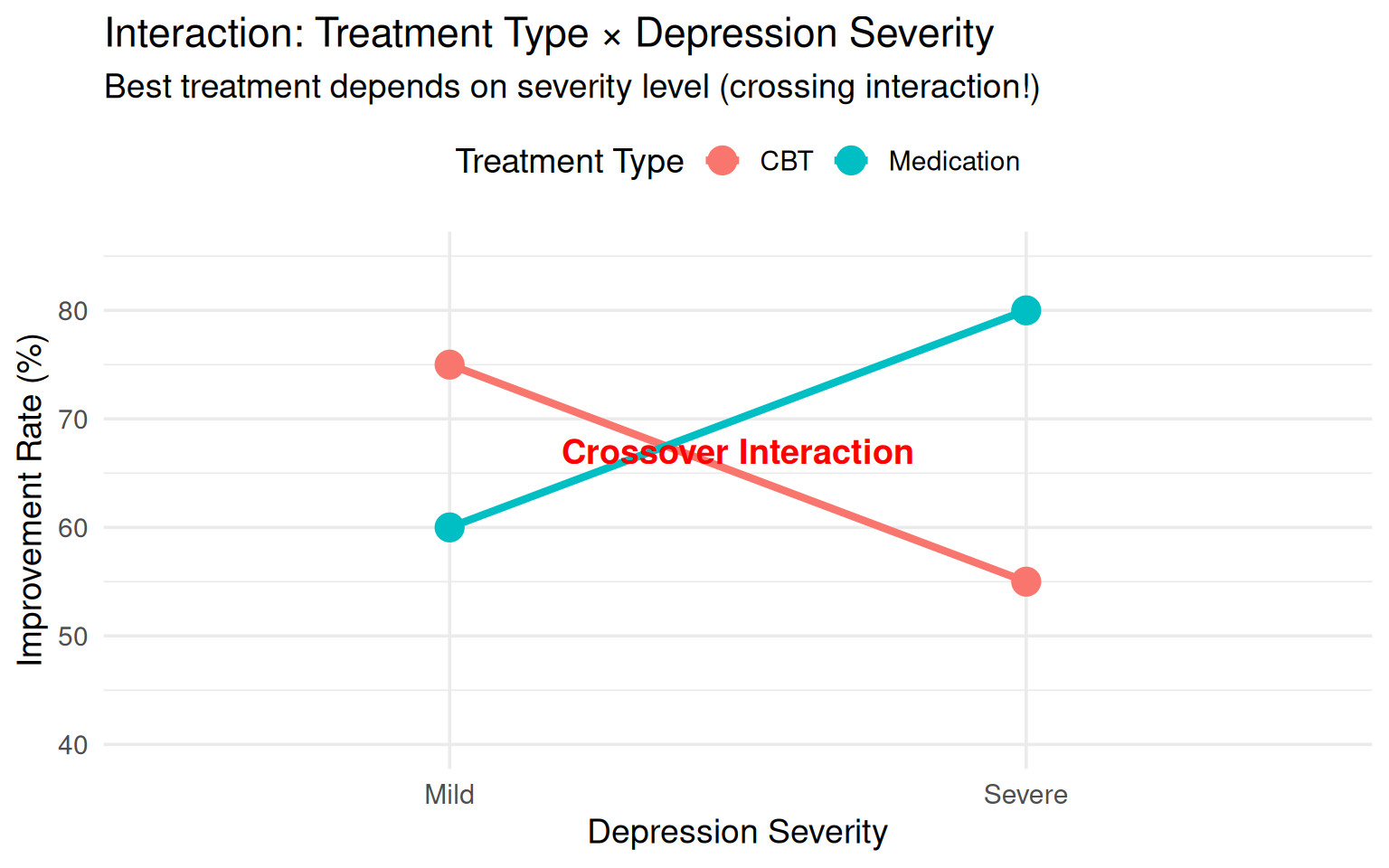
Research Question: Does the effectiveness of therapy type depend on depression severity?

Factors:

  • Factor A: Therapy Type (CBT vs. Medication)
  • Factor B: Depression Severity (Mild vs. Severe)

Observed Pattern (Interaction Present):

  • Mild Depression: CBT >> Medication (75% vs. 60% improvement)
  • Severe Depression: Medication >> CBT (80% vs. 55% improvement)

Why the interaction?

  • Mild depression patients can engage effectively with cognitive strategies in CBT
  • Severe depression patients may lack energy/motivation for CBT homework
  • Severe cases need biological intervention (medication) to restore neurochemical balance
  • CBT requires cognitive capacity that may be impaired in severe depression

Implication: Treatment selection should be severity-matched, not preference-based alone.

Visualization:

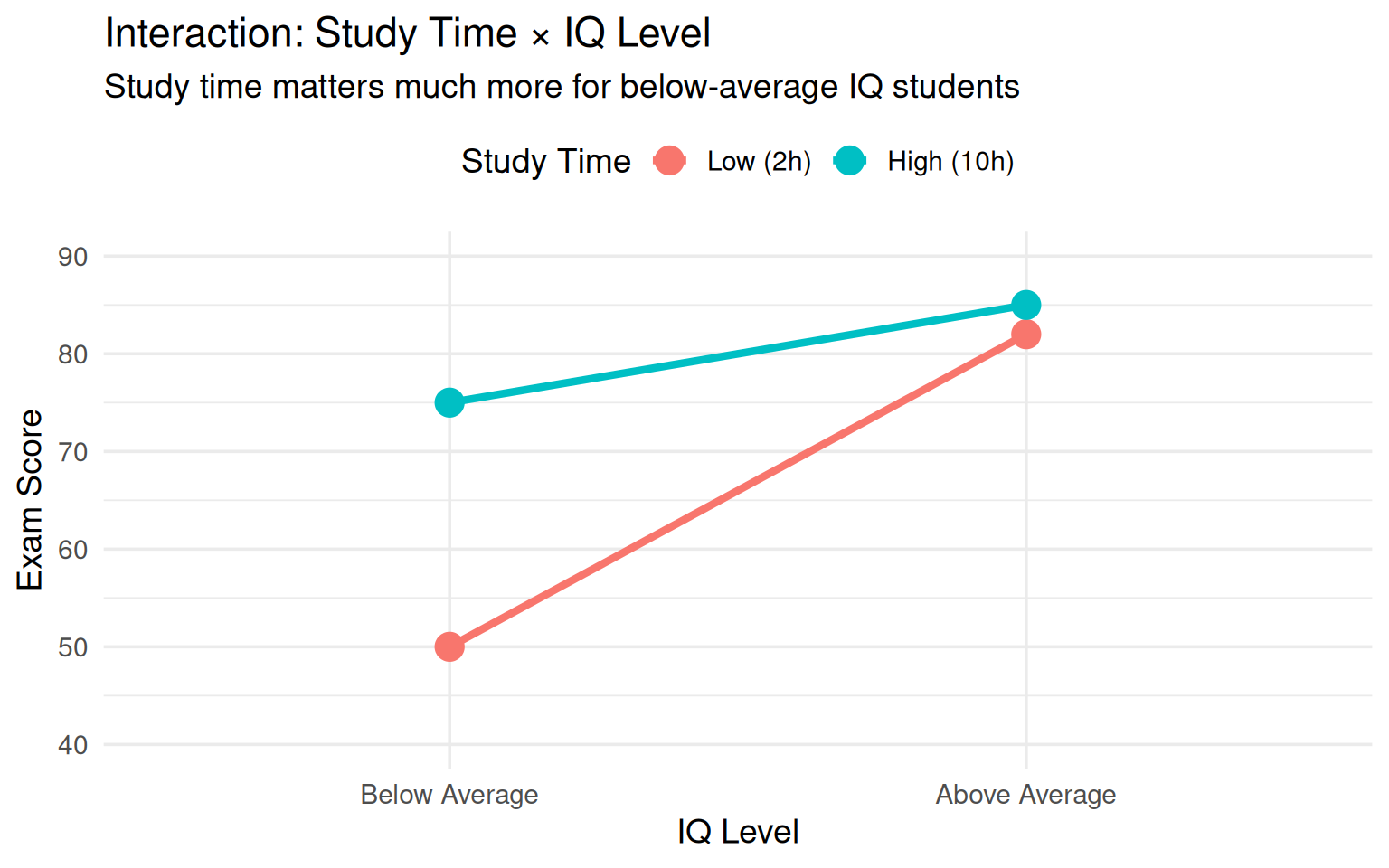
Research Question: Does the effect of study time on exam performance depend on intelligence level?

Factors:

  • Factor A: Study Time (Low: 2 hrs vs. High: 10 hrs)
  • Factor B: IQ Level (Below Average vs. Above Average)

Observed Pattern (Interaction Present):

  • Below Average IQ: High study time >> Low study time (75 vs. 50 points)
  • Above Average IQ: High study time ≈ Low study time (85 vs. 82 points)

Why the interaction?

  • High IQ students can learn material efficiently with less study time
  • Below average IQ students need more repetition and practice (more study time helps significantly)
  • High IQ students may reach a “ceiling effect” - already performing well with minimal study
  • Different cognitive abilities create different learning curves

Implication: Educational interventions (increasing study time) may be most beneficial for students who struggle, not top performers.

Visualization:

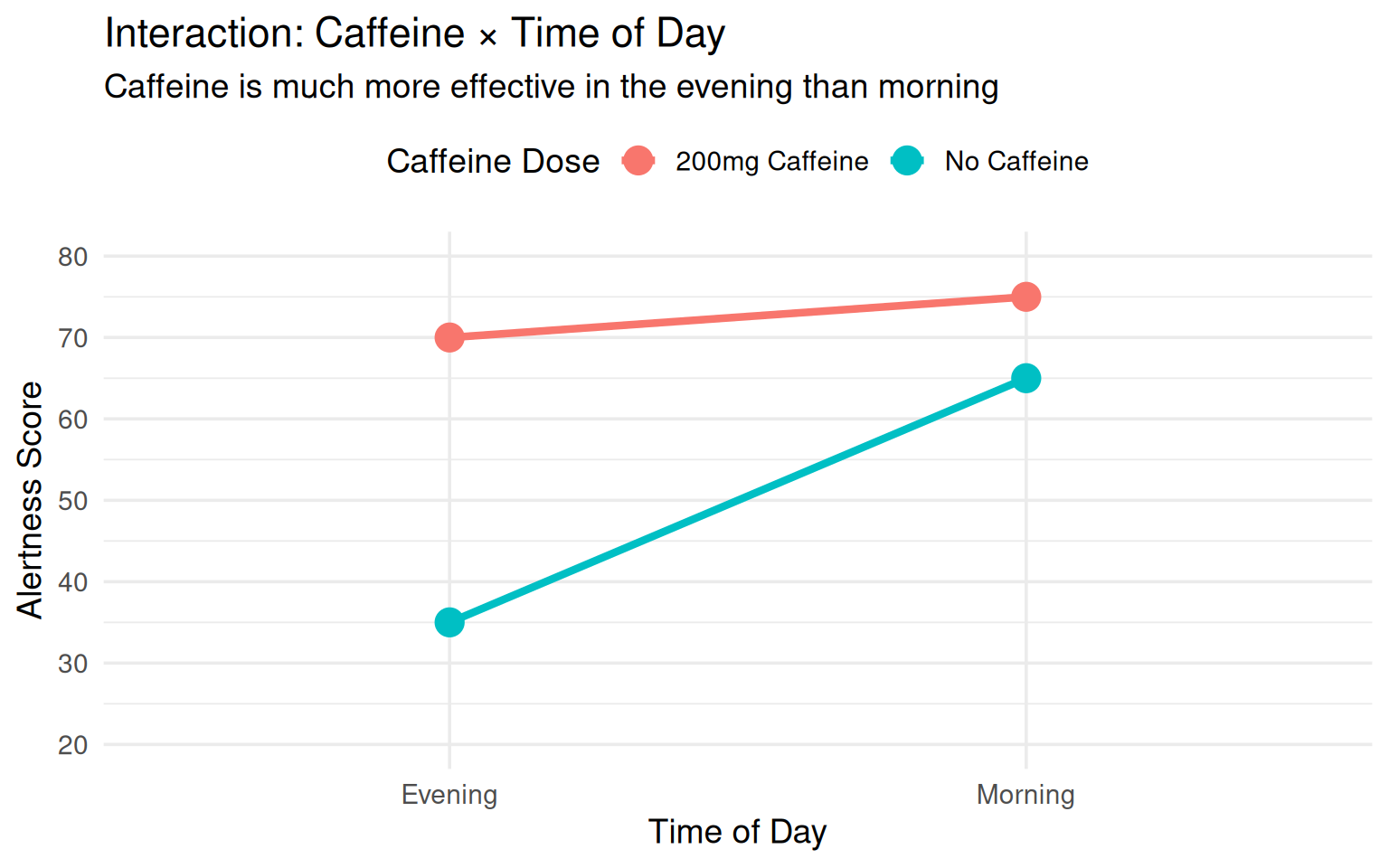
Research Question: Does caffeine’s effect on alertness depend on time of day?

Factors:

  • Factor A: Caffeine Dose (0 mg vs. 200 mg)
  • Factor B: Time of Day (Morning vs. Evening)

Observed Pattern (Interaction Present):

  • Morning: Small caffeine effect (alertness: 65 vs. 75)
  • Evening: Large caffeine effect (alertness: 35 vs. 70)

Why the interaction?

  • Morning: Natural cortisol levels are already high (circadian rhythm), so caffeine adds less
  • Evening: Cortisol levels drop naturally, so caffeine has a larger stimulating effect
  • Adenosine (sleepiness molecule) accumulates throughout the day - caffeine blocks adenosine receptors
  • Baseline alertness differs dramatically by time of day

Implication: Timing caffeine intake strategically (avoiding morning when cortisol is high) may be more effective.

Visualization:

Common Themes: Why Interactions Occur

Underlying Mechanisms for Interactions

  1. Biological Differences: Age, sex, genetics create different physiological responses
  2. Baseline/Ceiling Effects: Different starting points or maximum capacities across groups
  3. Mechanism Differences: Treatments work through different pathways in different populations
  4. Resource Allocation: Limited cognitive/physical resources are used differently across contexts
  5. Moderating Variables: Third variables (not measured) that correlate with factors
  6. Compensatory Strategies: Different groups adapt differently to interventions
  7. Dose-Response Variation: Sensitivity to “dosage” varies across groups

Critical Insight

Ignoring interactions leads to incorrect conclusions!

If you only report main effects in these examples, you would conclude:

  • “Drug A works” (missing that it works mainly for elderly)
  • “Problem-based learning is better” (missing that it depends on learning style)
  • “High intensity exercise is better” (missing that it mainly benefits males)

Always test and visualize interactions before interpreting main effects!

Model 2: Two-Way ANOVA with Interaction

\[ \mathrm{Grade} = U_1(\mathrm{Tutoring}) + U_2(\mathrm{School}) + U_3(\mathrm{TutoringxSchool}) \]

There variance components (random effects) included in a full two-way ANOVA with two Factors.

Model 2: Visualization of Two-Way ANOVA with Interaction

In the graph:

  • There is the LARGE effect of Factor A and very small effect of Factor B:
  • Effect of Factor A: the LARGE distance between two green stars
  • Effect of Factor B: the very small distance between two red stars

In the graph, there is an intersection between two lines → This is an interaction effect between two factors!

  • The level of Factor B depends upon the level of Factor A – B1 is higher than B2 for A1, but lower for A2 – B2 is lower than B1 for A1, but higher for A2

2 Statistical foundations of 2-way ANOVA

F-statistics for Two-Way ANOVA

F-statistics for Two-Way ANOVA: R code

Source df MS F
Main Effect of Tutoring 2 \(2120.1 = 4240 / 2\) 89.065***
Main Effect of School 2 \(10.8 = 22 / 2\) 0.636
Interaction Effect of School x Tutoring 4 \(46.5 = 186 / 4\) 0.102
Residual 261 \(23.8 = 6213 / 261\) —

F-statistics for Two-Way ANOVA: Degree of Freedom

  • IVs:
    1. Tutoring Programs: (1) No tutor; (2) Once a week; (3) Daily
    2. Types of schools: (1) Public (2) Private-secular (3) Private-religious
  • Degree of freedom (DF):
    • \(df_{tutoring}\) = (Number of levels of Tutoring) - 1 = 3 - 1 = 2
    • \(df_{school}\) = (Number of levels of School) - 1 = 3 - 1 = 2
    • \(df_{interaction}\) = \(df_{tutoring} \times df_{school}\) = \(2 \times 2\) = 4
    • \(df_{total}\) = 270 - 1 = 269
    • \(df_{residual}\) = \(df_{total}-df_{tutoring}-df_{school} - df_{interaction}\) = 269 - 2 - 2 - 4= 261

Calculation of p-values

Based on DF and observed F statistics, we can locate observed F-statistic onto the F-distribution can calculate the p-values.

F-statistics for Two-Way ANOVA: SS and DF

Why residual DF is calculated by subtracting the total DFs with effects’ DFs?

Because DF is linked to SS.

Source SS df
Main Effect of Tutoring 4240 2
Main Effect of School 22 2
Interaction Effect of School x Tutoring 186 4
Residual 6213 261
Total 4240 + 22 + 186 + 6213 2 + 2 + 4 + 261 
sum((data$Grades - mean(data$Grades))^2) # manually calculate total Sum of squares
nrow(data) - 1 # nrow() calculate the number of rows / observations
[1] 10660.77
[1] 269
4240 + 22 + 186 + 6213
2 + 2 + 4 + 261
[1] 10661
[1] 269

Difference between one-way and two-way ANOVA

One-way ANOVA

Total = Between + Within

Two-way ANOVA

Total = FactorA + FactorB + A*B + Residual

Within-factor effects (one-way ANOVA) and Residuals (two-way ANOVA) have same meaning, both of which are unexplained part of DV by the model.

  • In Factor ANOVA Design, the overall between-group variability is divided up into variance terms for each unique source of the factors.
Source 2 IVs 3 IVs 4 IVs
Main effect A, B A, B, C A, B, C, D
Interaction effect AB AB, BC, AC, ABC AB, AC, AD, BC, BD, CD, ABC, ABD, BCD, ACD, ABCD

Calculate the number of interaction effects \[ \mathrm{N_{interaction}} = \sum_{j=2}^J C_J^j \]

##Number of interaction for 4 IVs
choose(4, 2) + choose(4, 3) + choose(4, 4)
[1] 11

F-statistics for Two-way ANOVA: F values

  • F-observed values:

    • Main effect of factor A: \(F_A = \frac{SS_A/df_A}{SS_E/df_E} = \frac{MS_A}{MS_E}\)
      • \(F_{tutoring} = \frac{MS_{tutoring}}{MS_{residual}} = \frac{2120.1}{23.8} = 89.065\)
    • Main effect of factor B: \(F_B = \frac{MS_B}{MS_E}\)
      • \(F_{School} = \frac{MS_{School}}{MS_{residual}} = \frac{10.8}{23.8} = 0.453\)
    • Interaction effect of AxB: \(F_{AB} = \frac{MS_{AB}}{MS_E}\)
      • \(F_{SxT} = \frac{MS_{SxT}}{MS_{residual}} = \frac{46.5}{23.8} = 1.953\)

  • Degree of freedom:

    • \(df_{tutoring}\) = (Number of levels of Tutoring) - 1
    • \(df_{school}\) = (Number of levels of School) - 1
    • \(df_{interaction}\) = \(df_{tutoring} \times df_{school}\)
    • \(df_{total}\) = N - 1
    • \(df_{residual}\) = \(df_{total}-df_{tutoring}-df_{school} - df_{interaction}\)

Exercise

  • A new samples with N = 300
    • Tutoring still has three levels,
    • School types only have two levels: Public vs. Private.

Based on the SS provide below, calculate DF and F values for three effects.

F-statistics for Two-way ANOVA: Sum of squres

Note

In a old-fashion way, you can calculate Sum of Squares based on marginal means and sample size for each cell.

Interpretation

Source Df Sum Sq Mean Sq F value P
Tutoring 2 4240 2120.1 89.065 <2e-16 ***
School 2 22 10.8 0.453 0.636
Tutoring:School 4 186 46.5 1.953 0.102
Residuals 261 6213 23.8
  • Main Effect A: Ignoring type of school, are there differences in grades across type of tutoring?
    • Under alpha=.05 level, because F-observed (F_observed=89.065) exceeds the critical value (p < .001), we reject the null that all means are equal across tutoring type (ignoring the effect of school type).
    • There is a significant main effect of tutoring type on grade.
  • Main Effect B: Ignoring tutoring type, are there differences in grades across type of school?
    • Under alpha=.05 level, because F-observed (F_observed=95.40) exceeds the critical value (p = .453), we retain (or fail to reject) the null hypothesis that all means are equal across school type (ignoring the effect of tutoring type).
    • There is no evidence suggesting a significant main effect of school type on grade.
  • Interaction Effect: Does the effect of tutoring type on grades depend on the type of school?
    • Under alpha=.05 level, because F-observed (F_observed=2.21) does not exceed the critical value (p = 0.102), we fail to reject the null that the effect of Factor A depends on Factor B.
    • There is not a significant interaction between tutoring type and school type on grades.

Assumptions for conducting 2-way ANOVA

  • In order to compare our sample to the null distribution, we need to make sure we are meeting some assumptions for each CELL:
    1. Variance of DV in each cell is about equal. → Homogeneity of variance
    2. DV is normally distributed within each cell. → Normality
    3. Observations are independent. → Independence
  • Robustness of assumption violations:
    1. Violations of independence assumption: bad news! → Not robust to this!
    2. Having a large N and equal cell sizes protects you against violations of the normality assumption → Rough suggestion: have at least 15 participants per cell → If you don’t have large N or equal groups, check cell normality 2 ways: (1) skew/kurtosis values, (2) histograms
    3. Use Levene’s test to check homogeneity of cell variance assumption → If can’t assume equal variances, use Welch or Brown-Forsyth. → However, F is somewhat robust to violations of HOV as long as within-cell standard deviations are approximately equal.

Two-way ANOVA: Calculation based on Grand & Marginal & Cell Means

This research study is an adaptation of Gueguen (2012) described in Andy Field’s text. Specifically, the researchers hypothesized that people with tattoos and piercings were more likely to engage in riskier behavior than those without tattoos and piercings. In addition, the researcher wondered whether this difference varied, depending on whether a person was male or female.

Question: How many IVs? How many levels for each.

Answer: 2 IVs: (1) Whether or not having Tattos and Piercings (2) Male of Female. DV: Frequency of risk behaviors

Step 1: Data importing

Either you can import a CSV file, or manually import the data points (for small samples).

Imagine you have a data with N = 16.

tatto_piercing = rep(c(TRUE, FALSE), each = 8)
gender = rep(c("Male", "Female", "Male", "Female"), each = 4)
outcome = c(5.4, 6.7, 1.8, 6.1, 5.9, 4.6, 2.7, 3.8,
            2.6, 5.8, 1.5, 2.1, .6, .7, .7, 1.8)

dat <- data.frame(
  tatto_piercing = tatto_piercing,
  gender = gender,
  outcome = outcome
)
dat
   tatto_piercing gender outcome
1            TRUE   Male     5.4
2            TRUE   Male     6.7
3            TRUE   Male     1.8
4            TRUE   Male     6.1
5            TRUE Female     5.9
6            TRUE Female     4.6
7            TRUE Female     2.7
8            TRUE Female     3.8
9           FALSE   Male     2.6
10          FALSE   Male     5.8
11          FALSE   Male     1.5
12          FALSE   Male     2.1
13          FALSE Female     0.6
14          FALSE Female     0.7
15          FALSE Female     0.7
16          FALSE Female     1.8

Step 2: Sum of Squares of main effects

\[ SS_A = \sum n_a (M_{Aa} - M_T)^2 \]

  • \(M_{Aa}\) marginal mean of main effect A at each level
  • \(n_a\): sample size for factor A at each level
  • \(M_T\): grand mean of outcome

Obtain sum of square of tatto piercing

Manual way

M_A_table <-  dat |>
  group_by(tatto_piercing) |>
  summarise(
    N = n(),
    Mean = mean(outcome)
  )
M_T = mean(dat$outcome)
M_A_table
# A tibble: 2 × 3
  tatto_piercing     N  Mean
  <lgl>          <int> <dbl>
1 FALSE              8  1.98
2 TRUE               8  4.62
M_A_table$N[1] * (M_A_table$Mean[1] - M_T)^2 +
  M_A_table$N[2] * (M_A_table$Mean[2] - M_T)^2
[1] 28.09

or

sum(M_A_table$N * (M_A_table$Mean - M_T)^2)
[1] 28.09

Your turn: Obtain sum of squares of gender

dat object has already been loaded into R. Please, calculate the gender’s sum of squares:

Step 3: Sum of Squares of interaction effect

\[ SS_{AB} = (\sum n_{ab} (M_{AaBb} - M_T)^2) - SS_A - SS_B \]

cell_means <- dat |>
  group_by(tatto_piercing, gender) |>
  summarise(
    N = n(),
    Mean = mean(outcome)
  )
cell_means
# A tibble: 4 × 4
# Groups:   tatto_piercing [2]
  tatto_piercing gender     N  Mean
  <lgl>          <chr>  <int> <dbl>
1 FALSE          Female     4  0.95
2 FALSE          Male       4  3   
3 TRUE           Female     4  4.25
4 TRUE           Male       4  5

Your turn

The data frame — cell_means is already available to you.

Note: Sum of squares of interaction effects is the leftover of total sum of squares after removing SS of gender and SS of tutoring program.

\(SS_{total} = \Sigma (N_{ab} * (M_{ab} - M_T))\)

where \(N_{ab}\) is the cell sample size for a-level of factor A and b-level of factor B.

\(M_{ab}\) is the cell means of outcome; \(M_T\) is the grand mean of outcome.

Step 4: Calculate Degree of freedom and F-statistics

Interpretation

#                       Df Sum Sq Mean Sq F value Pr(>F)
# gender                 1   7.84   7.840   2.942  0.112
# tatto_piercing         1  28.09  28.090  10.540  0.007 **
# gender:tatto_piercing  1   1.69   1.690   0.634  0.441
# Residuals             12  31.98   2.665

  • Main Effect of Tattoo-Piercing: Reject the null → Ignoring the gender, there is a significant main effect of tattoo on risky behavior.

  • Main Effect of Gender: Retain the null → Ignoring the tattoo, there is NO significant main effect of gender on risky behavior.

  • Interaction: Retain the null → Under alpha=.05 level, because F-observed (F=0.63) does not exceed the critical value (F=4.75), we fail to reject the null that the effect of Factor A depends on Factor B. → “There is NO significant interaction between gender and tattoo on risky behavior.”

Final discussion

In this example,

  • The interaction effect shows several issues:

    • Violation of independency assumption
    • Violation of normality assumption in the condition of “Male” and “Tattoo=Yes”

  • We can guess/think about one possibility that it might be cause by several reasons. (e.g., too small sample sizes, not randomized assignments of the samples, not a significant interaction effect, etc.)

    • From the two-way ANOVA results, we found that the interaction effect is not significant.

  • Thus, in this case, it is more reasonable to conduct

    1. one-way ANOVA for “Group” variable, and
    2. one-way ANOVA for “Gender” variable, separately.
    • For each of one-way ANOVAs, we should check the assumptions, conduct one-way ANOVA, and post-hoc test separately as well.

Exercise: Two-Way ANOVA with Significant Interaction

A researcher is investigating the effect of learning environment (Online vs. In-Person) and feedback type (Immediate vs. Delayed) on student test scores. The researcher hypothesizes that:

  1. Students in in-person classes will perform better than online students
  2. Immediate feedback will lead to better performance than delayed feedback
  3. The benefit of immediate feedback will be stronger in online environments (interaction effect)

The study randomly assigned 20 students to one of four conditions:

  • Online + Immediate Feedback (n=5)
  • Online + Delayed Feedback (n=5)
  • In-Person + Immediate Feedback (n=5)
  • In-Person + Delayed Feedback (n=5)

Your Task: Calculate the sum of squares for both main effects and the interaction effect manually, then compute F-statistics.

Formula: \(SS_A = \sum n_a (M_{Aa} - M_T)^2\)

where: - \(M_{Aa}\) = marginal mean of Learning Environment at each level - \(n_a\) = sample size for each level of Learning Environment - \(M_T\) = grand mean

Formula: \(SS_B = \sum n_b (M_{Bb} - M_T)^2\)

Formula: \(SS_{AB} = (\sum n_{ab} (M_{AaBb} - M_T)^2) - SS_A - SS_B\)

Key Findings:

  1. Main Effect of Learning Environment: The effect depends on whether it’s significant (check your F-statistic and p-value)

  2. Main Effect of Feedback Type: The effect depends on whether it’s significant (check your F-statistic and p-value)

  3. Interaction Effect: This should be significant! The interaction plot shows that:

    • In Online environments, Immediate feedback leads to MUCH higher scores than Delayed feedback
    • In In-Person environments, the difference between Immediate and Delayed feedback is smaller (and reversed!)
    • This crossing pattern indicates a strong interaction: the effect of feedback type depends on the learning environment

Lecture Summary: Key Takeaways

1. Conceptual Understanding

Two-way ANOVA allows us to:

  • Examine the effects of two independent variables simultaneously
  • Test for three distinct effects: Main effect A, Main effect B, and Interaction A×B
  • Investigate whether the effect of one factor depends on the level of another factor (interaction)
  • Achieve greater statistical power and efficiency compared to multiple one-way ANOVAs

Main Effects vs. Interaction:

  • Main Effect: The average effect of one factor, ignoring (collapsing across) the other factor
  • Interaction Effect: When the effect of one factor changes depending on the level of the other factor
    • Look for non-parallel lines in interaction plots
    • Crossing lines indicate strong interactions
    • When interaction is significant, main effects may be misleading!

2. Statistical Calculations

Partitioning Variance in Two-Way ANOVA:

\[ SS_{Total} = SS_A + SS_B + SS_{AB} + SS_{Residual} \]

Key Formulas:

  • Main Effect A: \(SS_A = \sum n_a (M_{Aa} - M_T)^2\)
  • Main Effect B: \(SS_B = \sum n_b (M_{Bb} - M_T)^2\)
  • Interaction: \(SS_{AB} = (\sum n_{ab} (M_{AaBb} - M_T)^2) - SS_A - SS_B\)

F-statistics:

\[ F = \frac{MS_{effect}}{MS_{residual}} = \frac{SS_{effect}/df_{effect}}{SS_{residual}/df_{residual}} \]

Degrees of Freedom:

  • \(df_A = k_A - 1\) (number of levels of Factor A minus 1)
  • \(df_B = k_B - 1\) (number of levels of Factor B minus 1)
  • \(df_{AB} = df_A \times df_B\) (interaction df)
  • \(df_{residual} = N - 1 - df_A - df_B - df_{AB}\)

3. Practical Considerations

Assumptions for Two-Way ANOVA:

  1. Independence: Observations must be independent (most critical!)
  2. Normality: DV should be normally distributed within each cell
  3. Homogeneity of Variance: Equal variances across all cells (Levene’s test)

Robustness:

  • F-test is fairly robust to normality violations with large N and equal cell sizes
  • Recommend at least 15 participants per cell
  • Use Welch or Brown-Forsythe tests if variances are unequal
  • Never compromise on independence assumption

Type I, II, III Sum of Squares:

  • Type I: Sequential (order matters) - appropriate for nested/blocking designs
  • Type II: Each main effect adjusted for other main effects - good for model building
  • Type III: Each effect adjusted for all others - recommended for factorial designs with balanced data
  • With balanced designs (equal cell sizes), all three types give identical results!

4. Interpretation Guidelines

When Interaction is Significant:

  • Interpret interaction first before discussing main effects
  • Main effects may be misleading or uninterpretable when interaction is present
  • Focus on simple effects: the effect of one factor at each level of the other
  • Use interaction plots to visualize and explain the pattern

When Interaction is NOT Significant:

  • Proceed to interpret main effects
  • If main effect is significant with >2 levels, conduct post-hoc tests (e.g., Tukey HSD)
  • Report effect sizes (partial η²) alongside p-values

Reporting Results:

Include in your report:

  1. Descriptive statistics (means, SDs) for all cells
  2. ANOVA table with F-values, df, and p-values
  3. Effect sizes
  4. Interaction plot (even if not significant)
  5. Post-hoc tests if needed
  6. Assumption checks

5. Common Pitfalls to Avoid

  1. Don’t ignore significant interactions! Main effects alone don’t tell the whole story
  2. Don’t forget assumption checks - especially for small samples
  3. Don’t confuse interaction with correlation - they are different concepts
  4. Don’t over-interpret non-significant results - absence of evidence ≠ evidence of absence
  5. Don’t use multiple one-way ANOVAs instead of two-way - you’ll miss interactions and inflate Type I error
  6. Don’t forget to report effect sizes - statistical significance ≠ practical significance

6. Next Steps in Your Learning

Extending Two-Way ANOVA:

  • Three-way ANOVA: Adding a third factor (exponentially more complex!)
  • Mixed ANOVA: Combining between-subjects and within-subjects factors
  • ANCOVA: Adding continuous covariates to control for confounding variables
  • MANOVA: Multiple dependent variables simultaneously
  • Repeated Measures ANOVA: Same subjects measured multiple times

When to Use Two-Way ANOVA:

✓ Two categorical independent variables (factors) ✓ One continuous dependent variable ✓ Independent observations (between-subjects design) ✓ Interest in both main effects and interaction ✓ Adequate sample size (≥15 per cell recommended)

Alternatives to Consider:

  • Regression with interactions: More flexible, can handle continuous IVs
  • Mixed-effects models: Better for unbalanced designs or nested data
  • Non-parametric tests: When assumptions are severely violated (e.g., Aligned Rank Transform ANOVA)

Fin

Thank you for your attention!