Large Language Models

1 Model architecture

1.1 Transformer

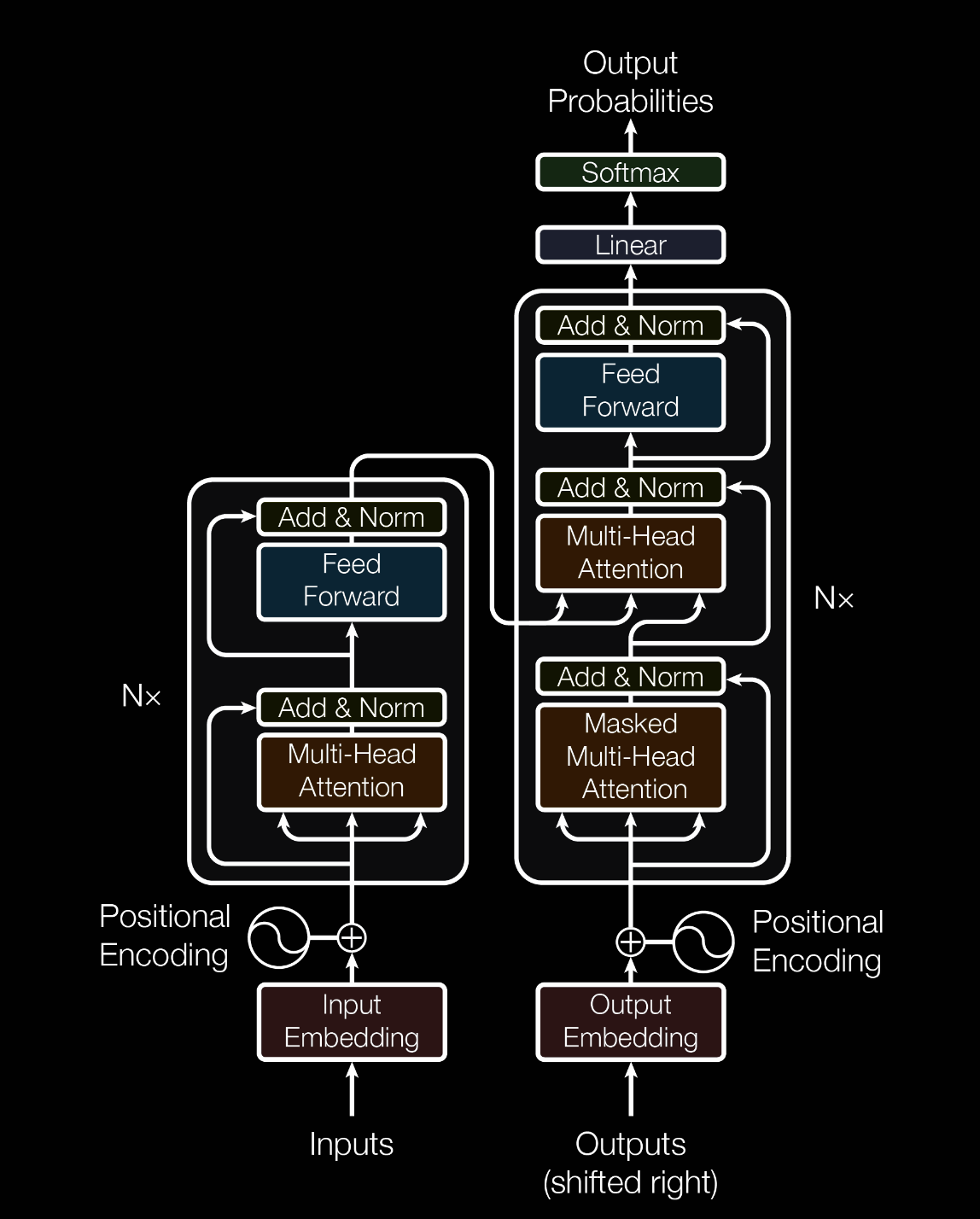
The original Transformer architecture was introduced in the paper Attention is All You Need by Vaswani et al. in 2017. The Transformer model has since become the foundation for many state-of-the-art natural language processing (NLP) models, including BERT, GPT-3, and T5.

1.1.1 Terminology

• Self-attention: an attention mechanism relating different positions of a single sequence to compute a representation of the sequence.

  • Q,K,V matrix: query, keys, values. The output is computed as a weighted sum of the values. All these three are key component of Attention function. The following formula is also known as Scaled dot-product attention.

    $$\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$$

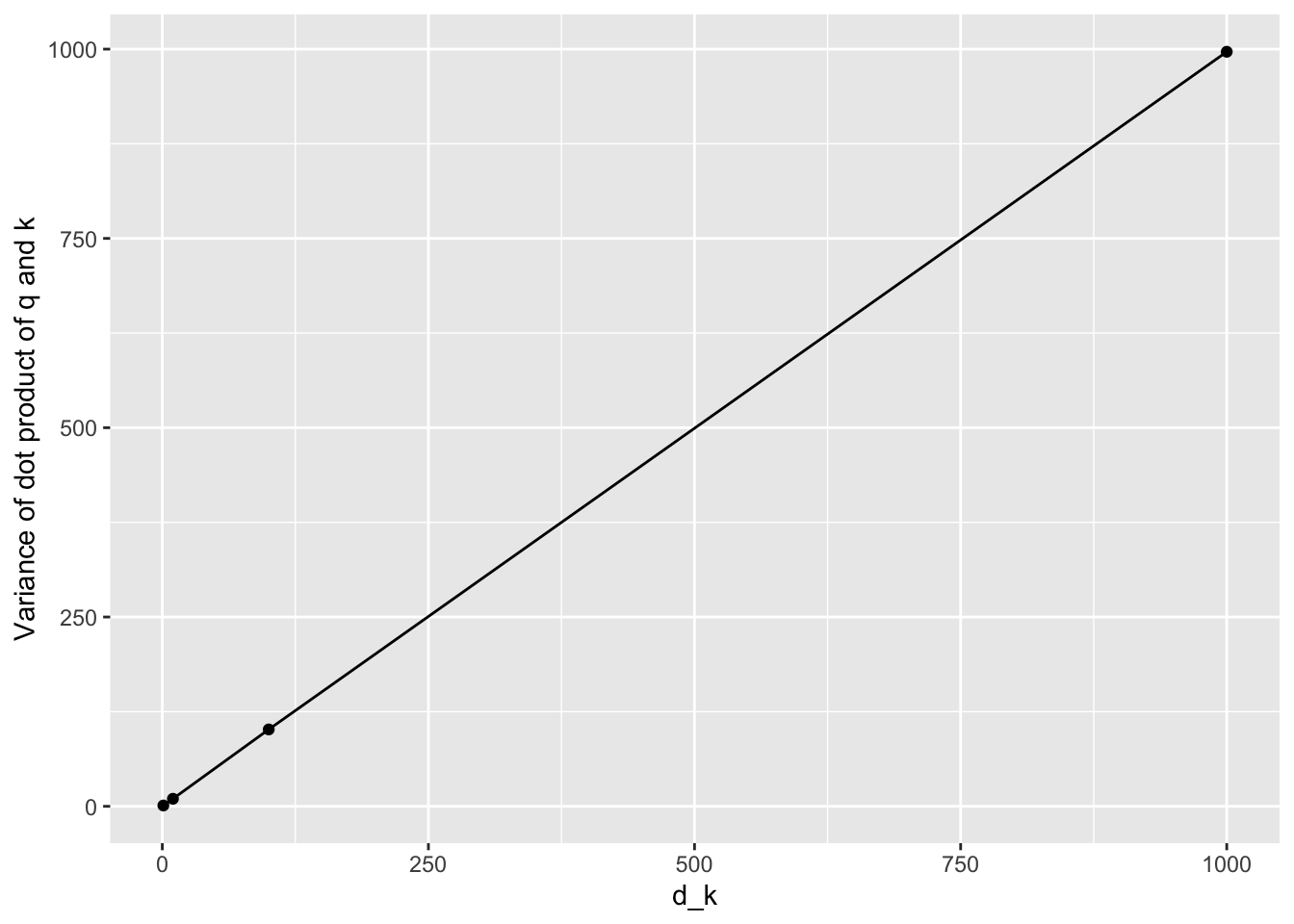
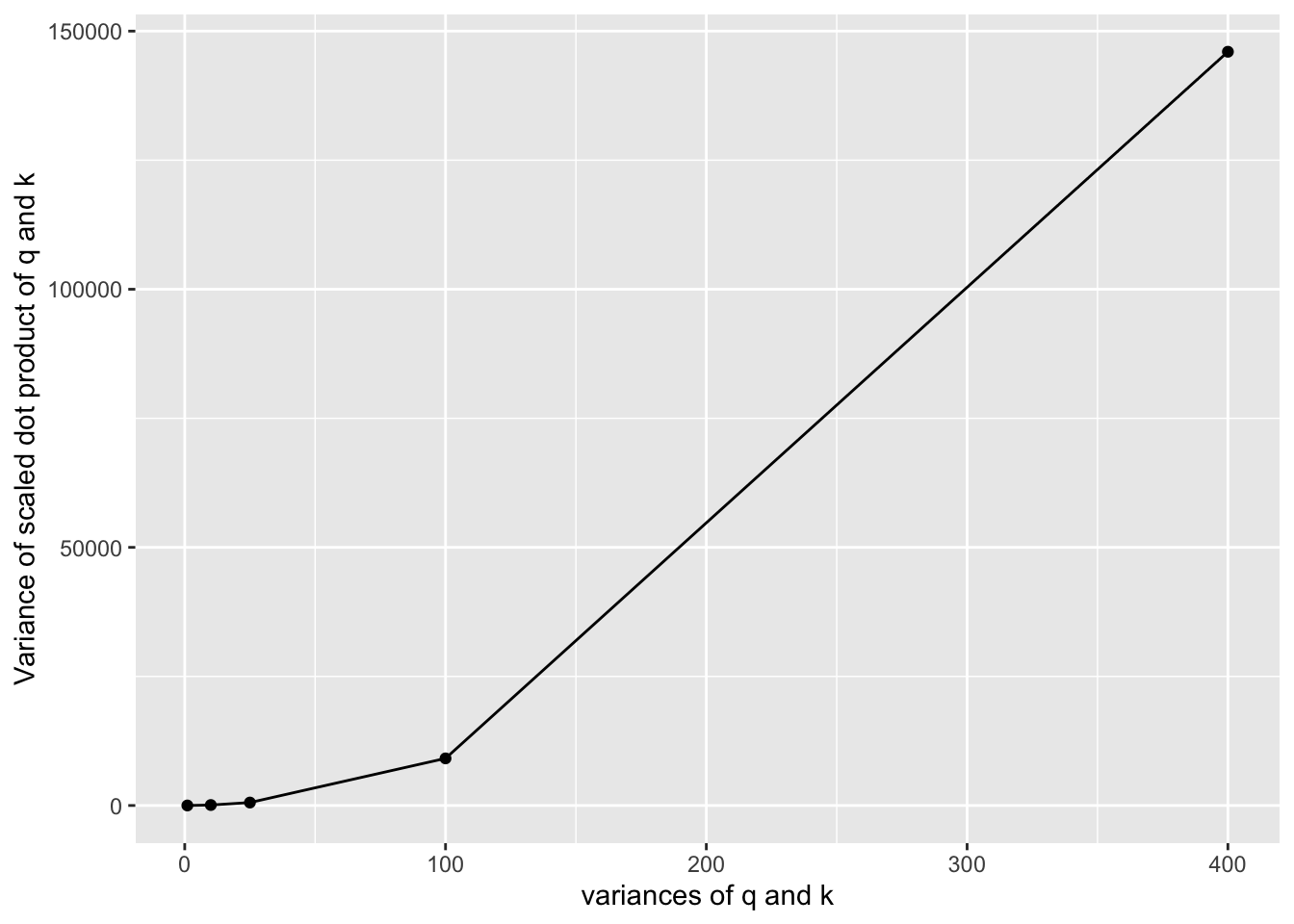
  • where queries and keys have the dimension $d_k$

the dot products get larger variances when the dimension of q and k increase. So they scale the dot product by $\frac{1}{\sqrt{d_k}}$ to make sure the dot product has close variance with q and k.

library(ggplot2)
N_rep = 1000
dot_product <- function(i, d_k, var_q = 1) {
  set.seed(i)
  q = rnorm(d_k, 0, sd = sqrt(var_q))
  k = rnorm(d_k, 0, sd = sqrt(var_q))
  crossprod(q, k)
}

var_dot_product <- function(N_rep, d_k, var_q = 1) {
  dot_product_values <- sapply(1:N_rep, \(x) dot_product(x, d_k = d_k, var_q))
  var(dot_product_values)
}

to_plot <- data.frame(
  d_k_values = c(1, 10, 100, 1000),
  var_dot_product_values = sapply(c(1, 10, 100, 1000), \(x) var_dot_product(N_rep = N_rep, 
                                                                   d_k = x))
)

ggplot(to_plot, aes(x = d_k_values, y = var_dot_product_values)) +
  geom_path() +
  geom_point() +
  labs(x = "d_k", y = "Variance of dot product of q and k")

var_q_values = c(1, 10, 25, 100, 400) # variances of q and k
d_k = 2 # dimension of k

# function to generate the variaance of scaled dot products
var_scaled_dot_product <- function(N_rep, d_k, var_q = 1) {
  scaled_dot_product_values <- sapply(1:N_rep,\(x){dot_product(x, d_k = d_k, var_q = var_q)/sqrt(d_k)} )
  var(scaled_dot_product_values)
}

var_scaled_dot_product_values <- sapply(var_q_values, 
                                        \(x) var_scaled_dot_product(N_rep = N_rep, 
                                                                    d_k = d_k, 
                                                                    var_q = x) )

data.frame(
  var_q_values = var_q_values,
  var_scaled_dot_product_values = var_scaled_dot_product_values
) |> 
ggplot(aes(x = var_q_values, y = var_scaled_dot_product_values)) +
  geom_path() +
  geom_point() +
  labs(x = "variances of q and k", y = "Variance of scaled dot product of q and k")

• Multi-Head Attention:

• Encoder-decoder structure: The basic structure of most neural sequence transduction models.

  • Encoder maps an input to a sequence of continuous representations.

  • Decoder generates an output sequence given the continuous representation of encoder

The Transformer - model architecture in the original paper

2 Evaluation metrics

2.1 Item Similarity

Various metrics can be used to evaluate the similarity between two sentences (e.g., math items) at the lexical level. They are typically called vector similarity measures.

2.1.1 BLEU

BLEU (Bilingual Evaluation Understudy) is a metric for evaluating the quality of text that has been machine-translated from one natural language to another (see geeksforgeeks). It compares a candidate translation to one or more reference translations and calculates a score based on the overlap of n-grams (contiguous sequences of n items) between the candidate and reference translations. Higher values indicate better quality translations.

The formula of BLEU score is:

$$\text{BLEU}(C, R) = BP \cdot \exp\left(\sum_{n=1}^{N} w_n \cdot \log p_n\right)$$

where:

• $C$ is the candidate translation,
• $R$ is the reference translation,
• $BP$ is the brevity penalty, which penalizes translations that are shorter than the reference translation,
• $p_n$ is the precision of n-grams in the candidate translation,
• $w_n$ is the weight assigned to the n-gram precision, typically set to $\frac{1}{N}$ for $n=1,2,\ldots,N$.

from nltk.translate.bleu_score import sentence_bleu, SmoothingFunction
def calculate_bleu(candidate, reference):
    # Tokenize the sentences
    candidate_tokens = candidate.split()
    reference_tokens = reference.split()
    
    # Calculate BLEU score
    smoothing_function = SmoothingFunction().method1
    bleu_score = sentence_bleu([reference_tokens], candidate_tokens, smoothing_function=smoothing_function)
    
    return bleu_score

candidate = "The cat sat on the mat."
reference = "The cat is sitting on the mat."

bleu_score = calculate_bleu(candidate, reference)
print(f"BLEU score: {bleu_score:.4f}")

BLEU score: 0.2151

2.1.2 Cosine Similarity

The cosine similarity is a measure of similarity between two non-zero vectors of an inner product space that measures the cosine of the angle between them. In NLP, it is often used to compare the similarity of two text documents or sentences by representing them as vectors in a high-dimensional space.

The formula of the cosine similarity is:

$$\text{cosine\_similarity}(A, B) = \frac{A \cdot B}{||A|| \cdot ||B||}$$

where $A$ and $B$ are the two vectors, $A \cdot B$ is the dot product of the vectors, and $||A||$ and $||B||$ are the magnitudes (or norms) of the vectors.

To convert words into vectors, we can use a simple method called word2vec. To be more specific, we can represent a word as a vector of character frequencies, where each character in the word is counted and represented as a dimension in the vector space.

Python

def word2vec(word):
    from collections import Counter
    from math import sqrt

    # count the characters in word
    cw = Counter(word)
    # precomputes a set of the different characters
    sw = set(cw)
    # precomputes the "length" of the word vector
    lw = sqrt(sum(c*c for c in cw.values()))

    # return a tuple
    return cw, sw, lw

def cosdis(v1, v2):
    # which characters are common to the two words?
    common = v1[1].intersection(v2[1])
    # by definition of cosine distance we have
    return sum(v1[0][ch]*v2[0][ch] for ch in common)/v1[2]/v2[2]
  
a = 'Problem: Ten people are sitting around a round  table. Three of them are chosen at random to give  a presentation. What is the probability that the  three chosen people were sitting in consecutive  seats?'
b = 'Problem: Ten people are sitting around a round table. Three of  them are chosen at random to give a presentation in a specific  order. What is the probability that the first and second presenter  were sitting in consecutive seats and at the same time the second  and third presenter were sitting in consecutive seats?'
c = 'Problem: Ten people are sitting around a round table. Four of them are chosen at random to give a presentation in a specific order. What is the probability that the first and second presenter were sitting in consecutive seats and at the same time the second and third presenter were sitting in consecutive seats?'

va = word2vec(a)
vb = word2vec(b)
vc = word2vec(c)

print(cosdis(va,vb))

0.9901018675724259

print(cosdis(vb,vc))

0.9990936880256146

print(cosdis(vc,va))

0.988220284030085

R

a = 'Problem: Ten people are sitting around a round  table. Three of them are chosen at random to give  a presentation. What is the probability that the  three chosen people were sitting in consecutive  seats?'
b = 'Problem: Ten people are sitting around a round table. Three of  them are chosen at random to give a presentation in a specific  order. What is the probability that the first and second presenter  were sitting in consecutive seats and at the same time the second  and third presenter were sitting in consecutive seats?'
c = 'Problem: Ten people are sitting around a round table. Four of them are chosen at random to give a presentation in a specific order. What is the probability that the first and second presenter were sitting in consecutive seats and at the same time the second and third presenter were sitting in consecutive seats?'

cosine_similarity <- function(a, b) {
  a <- strsplit(a, "")[[1]]
  b <- strsplit(b, "")[[1]]
  
  a_freq <- table(a)
  b_freq <- table(b)
  
  common_chars <- intersect(names(a_freq), names(b_freq))
  
  dot_product <- sum(a_freq[common_chars] * b_freq[common_chars])
  norm_a <- sqrt(sum(a_freq^2))
  norm_b <- sqrt(sum(b_freq^2))
  
  return(dot_product / (norm_a * norm_b))
}

cosine_similarity(a, b)

[1] 0.9901019

cosine_similarity(b, c)

[1] 0.9990937

cosine_similarity(a, c)

[1] 0.9882203

2.1.3 Edit Similarity

3 Fail Mode Analysis

Fail mode analysis (FMA) is a systematic approach to identify potential failure modes in a system, process, or product and assess their impact on performance, safety, and reliability. It is commonly used in engineering and quality management to improve designs and processes by proactively addressing potential issues. FMA of LLMs can help identify potential failure modes in the model’s architecture, training data, and inference process, leading to improved performance and reliability.

There are various failure modes that can occur in LLMs, including:

1. Potemkin Understanding: the illusion of understanding driven by answers irreconcilable with how any human would interpret a concept(Mancoridis et al., 2025).

2. Overfitting: The model may become too specialized to the training data, resulting in poor generalization to new or unseen data. This can lead to a lack of robustness and adaptability in real-world applications. Recent works focus on using benchmarks with perturbations to test the robustness of LLMs, such as Huang et al. (2025).

3. Context Window Limitation: large reasoning models may fail to reason consistently in complex task, such as Tower of Hanai as shown in Shojaee et al. (2025). This may be because Chain-of-Thoughts (CoT) technique used by LRMs needs more steps in reasoning steps which is limited by the length of output tokens.

Mancoridis, M., Weeks, B., Vafa, K., & Mullainathan, S. (2025, June). Potemkin understanding in large language models. https://openreview.net/forum?id=oetxkccLoq

Huang, K., Guo, J., Li, Z., Ji, X., Ge, J., Li, W., Guo, Y., Cai, T., Yuan, H., Wang, R., & al., et. (2025). MATH-perturb: Benchmarking LLMs’ math reasoning abilities against hard perturbations. https://doi.org/10.48550/arXiv.2502.06453

Shojaee, P., Mirzadeh, I., Alizadeh, K., Horton, M., Bengio, S., & Farajtabar, M. (2025). The illusion of thinking: Understanding the strengths and limitations of reasoning models via the lens of problem complexity.

3.1 Potemkin understanding

Regarding concept understanding ability of LLMs, traditional measures use accuracy (%) of human assessments (AP exams, AIME math competitions, and coding challenges) as the indicator.

Human benchmarks are only valid tests for LLMs if LLMs misunderstand concepts in the same way that humans do.

However, LLMs may have different ways of understanding concepts than humans, leading to a mismatch in evaluation—LLMs may achieve high accuracy on human benchmarks while still misunderstanding concepts.

3.1.1 Reason

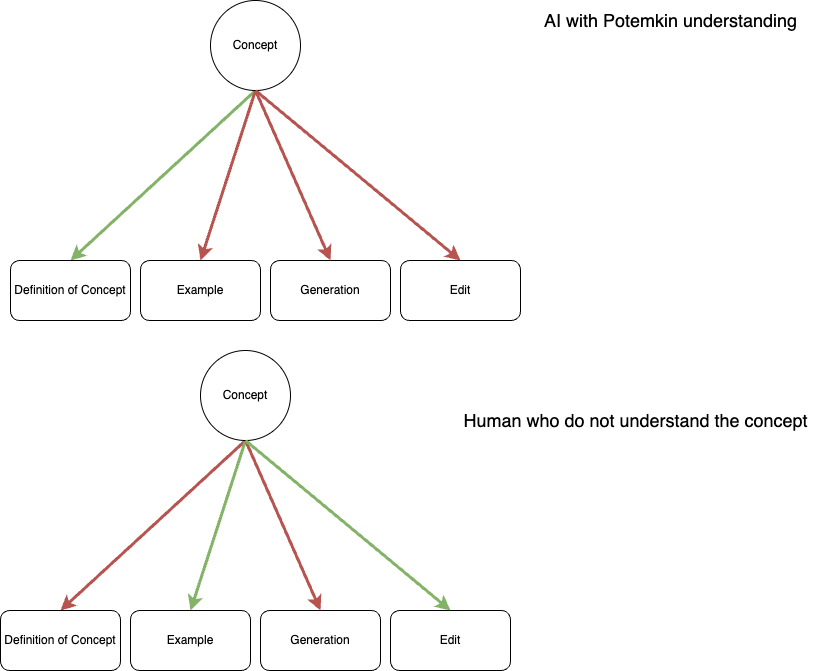
Potemkins arise when there is a misalignment between the way LLMs understand concepts and the way humans do. In the experiment of Mancoridis et al. (2025), they used the definition of the concept as keystone element. Then, the Potemkin refers to the incorrectly answering other types of instances (e.g., example, generation, and edit) while being able to correctly define the concept. They argued that human’s misconception is more structured, they may answers those instances correctly or incorrectly while they do not understand the underlying concept.

In the diagnostic classification models, human may also answer those questions incorrectly given his/her latent ability level. The chance of incorrectly answering the questions when they actually understanding the concepts is called slipping rate, denoted as $P(X = 0 | \alpha = 1)$. Based on the conception of Mancoridis et al. (2025), the slipping rate should be inconsistent across instance.

Keynote indicator for AI potemkins and Human misconceptions

Experiment: correct concept understanding

library(ellmer)
chat <- chat_openai()

user_prompt1 <- "
Fill in the blank so that the resultant poem uses the ABAB rhyming scheme:  
Wondrous winter calls out 
Shivering under the frost 
Lies a lonely cat, sitting ? 
Alone but hardly lost"
chat$chat(user_prompt1)

The rhyme scheme ABAB means that the second and fourth lines rhyme, and the 
first and third lines rhyme. In your poem, "out" (first line) needs to rhyme 
with the third line, and "frost" (second line) with the fourth line "lost". 
Since "sitting ?" (third line) should rhyme with "out", a suitable word would 
be "about."  

So the completed poem is:

Wondrous winter calls out  
Shivering under the frost  
Lies a lonely cat, sitting **about**  
Alone but hardly lost

user_prompt2 <- "What is an ABAB rhyming scheme?"
chat$chat(user_prompt2)

An **ABAB rhyming scheme** is a pattern used in poetry where the end words of 
certain lines rhyme in a specific order:

- The first and third lines rhyme with each other (A)
- The second and fourth lines rhyme with each other (B)

So, if you label each ending sound with a letter, the ABAB scheme looks like 
this:

```
Line 1 (A): Roses are red       ← (A)
Line 2 (B): Violets are blue   ← (B)
Line 3 (A): Sugar is sweet     ← (A)
Line 4 (B): And so are you     ← (B)
```

Here, "red" rhymes with "sweet" (in the example, it would need to be changed 
for an actual rhyme), and "blue" rhymes with "you." 

**Summary:**  
In an ABAB rhyme scheme, the first and third lines rhyme, and the second and 
fourth lines rhyme.

user_prompt3 <- "Does 'out' rhyme with 'soft'?"
chat$chat(user_prompt3)

No, **"out"** does not rhyme with **"soft."** 

- "Out" rhymes with words like "shout," "about," "doubt," etc.
- "Soft" rhymes with words like "loft," "cough" (British pronunciation), 
"croft," etc.

For two words to rhyme, their ending sounds need to match, especially from the 
vowel sound to the end of the word. "Out" ends with the "-out" sound, while 
"soft" ends with the "-oft" sound, so they do not rhyme.

Experiment: incorrect concept understanding

chat2 <- chat_openai(model = "gpt-3.5-turbo-1106")

#> Wondrous winter calls out 
#> Shivering under the frost 
#> Lies a lonely cat, sitting proud 
#> Alone but hardly lost

user_prompt2.3 <- "Does 'proud' rhyme with 'soft'?"

#> No, "proud" and "soft" do not rhyme with each other. Rhyme occurs when two or more words have similar sounds, especially at the end of the words. In the ABAB rhyming scheme, the second and fourth lines should rhyme with each other.