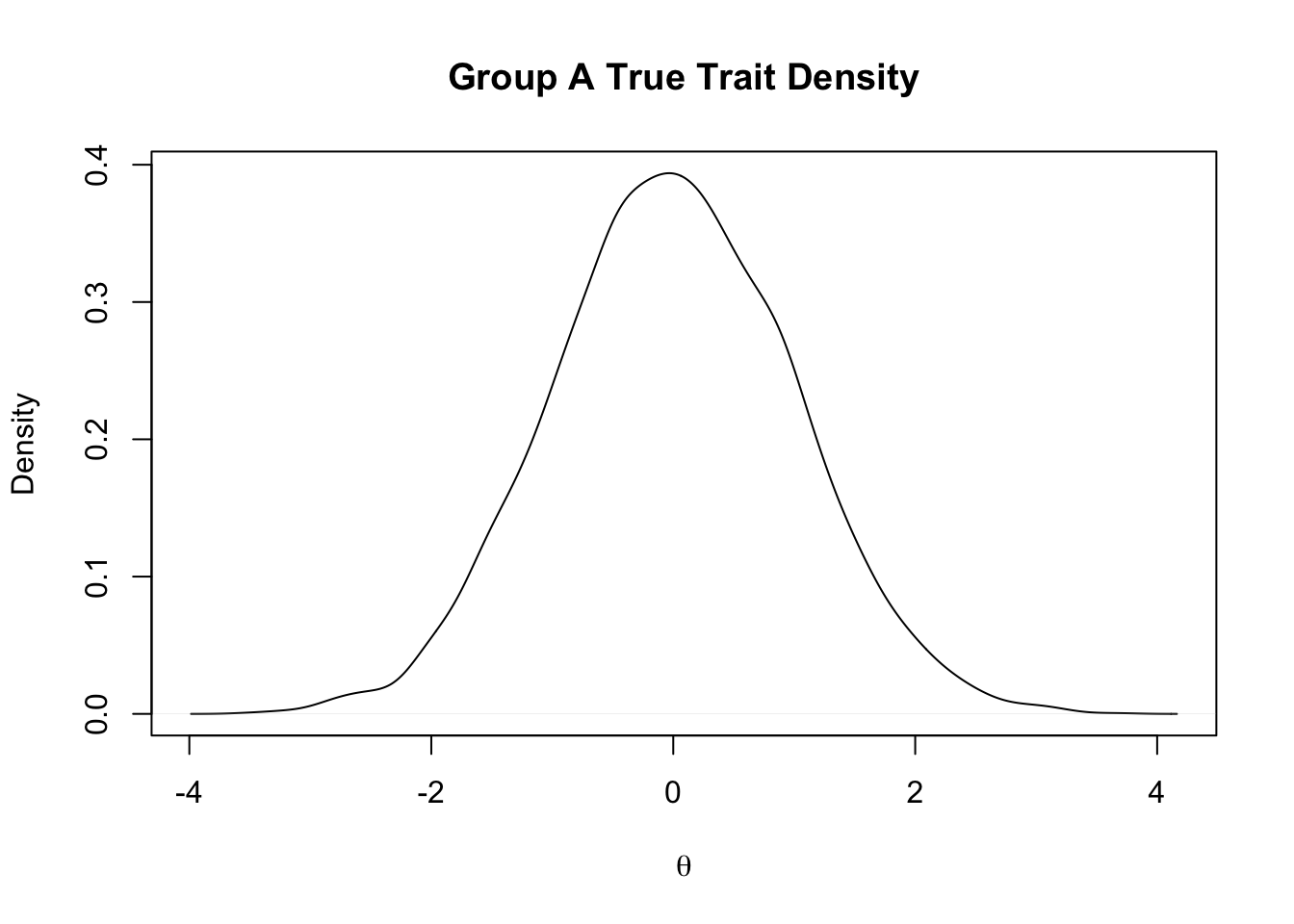
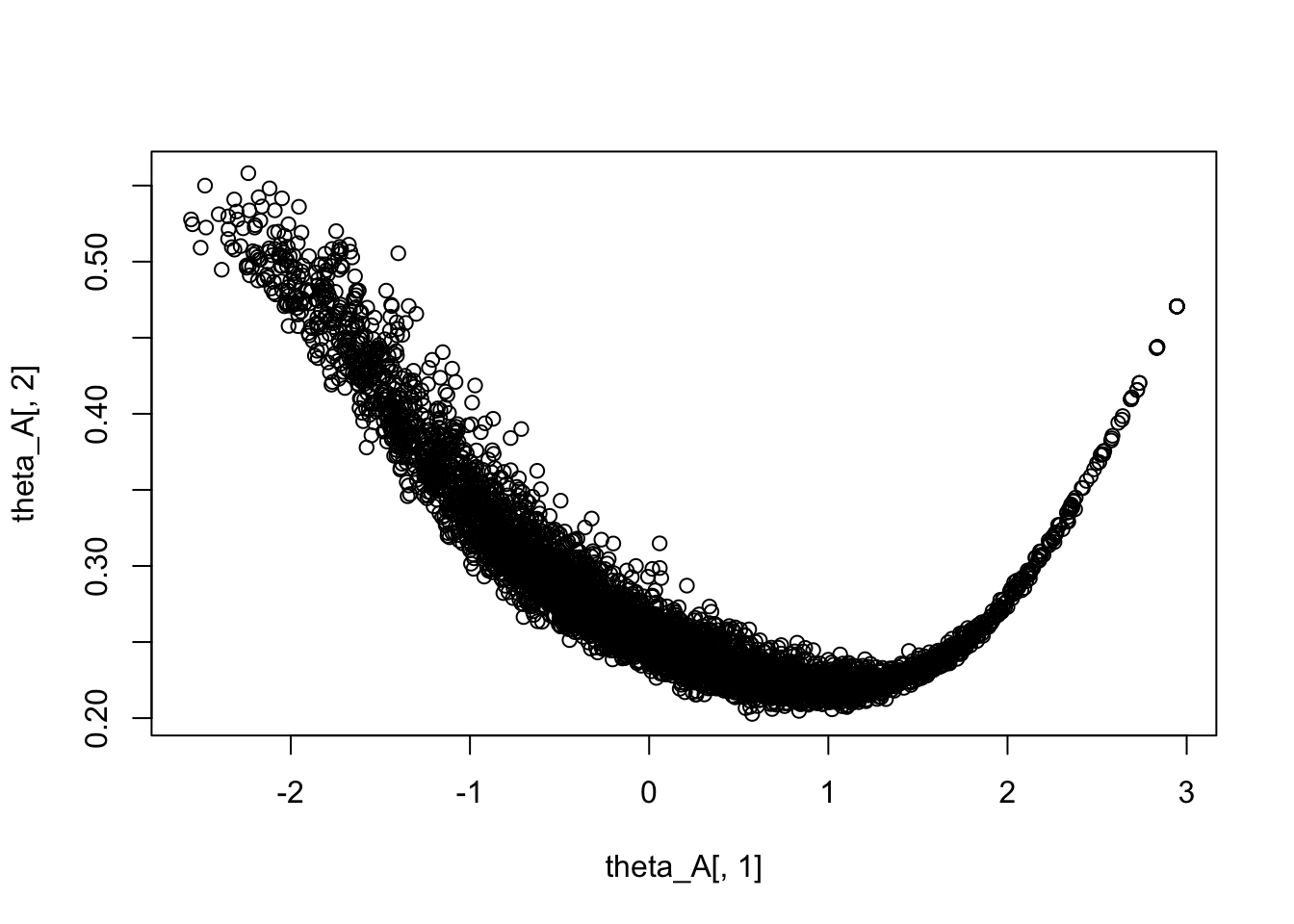
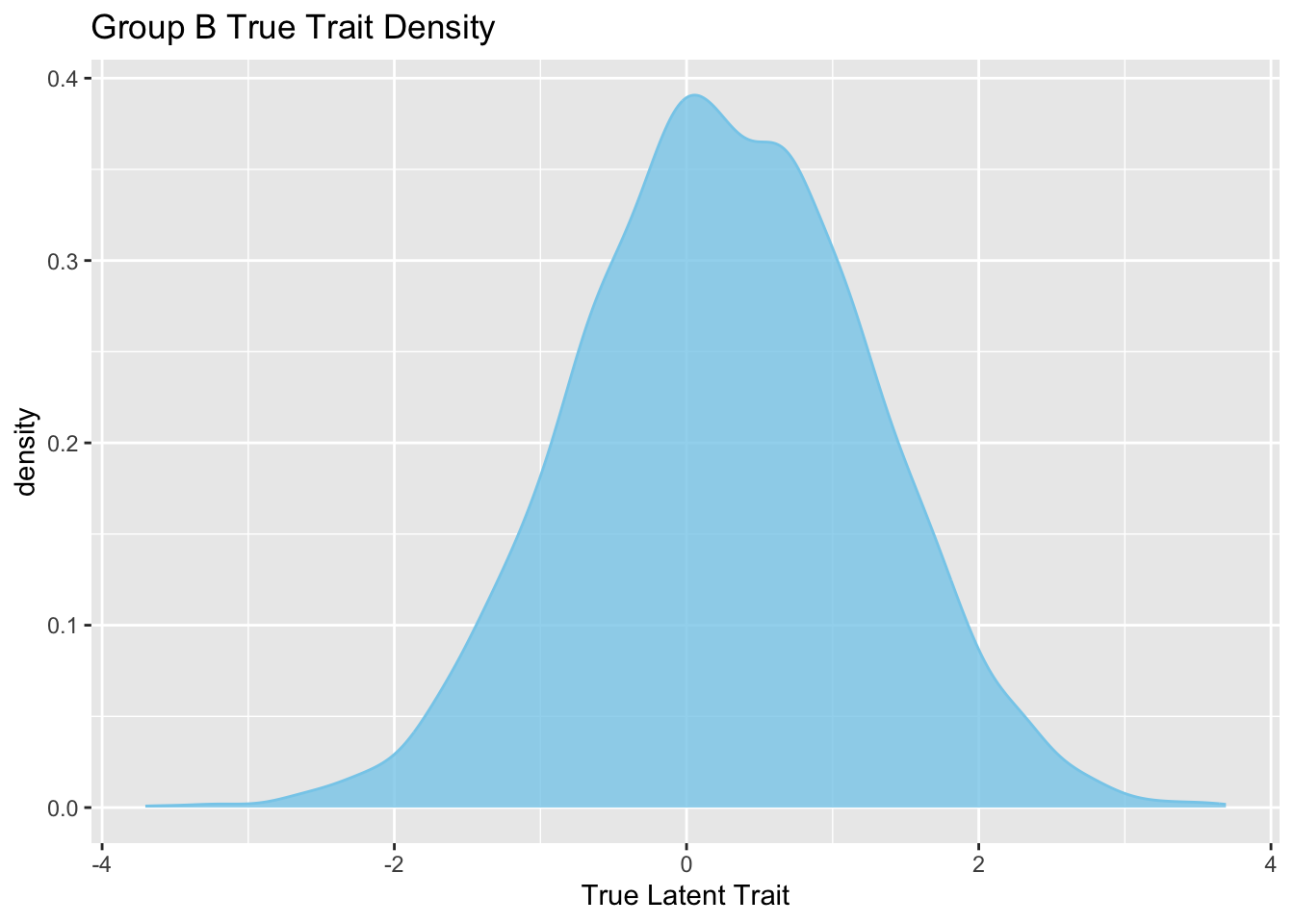
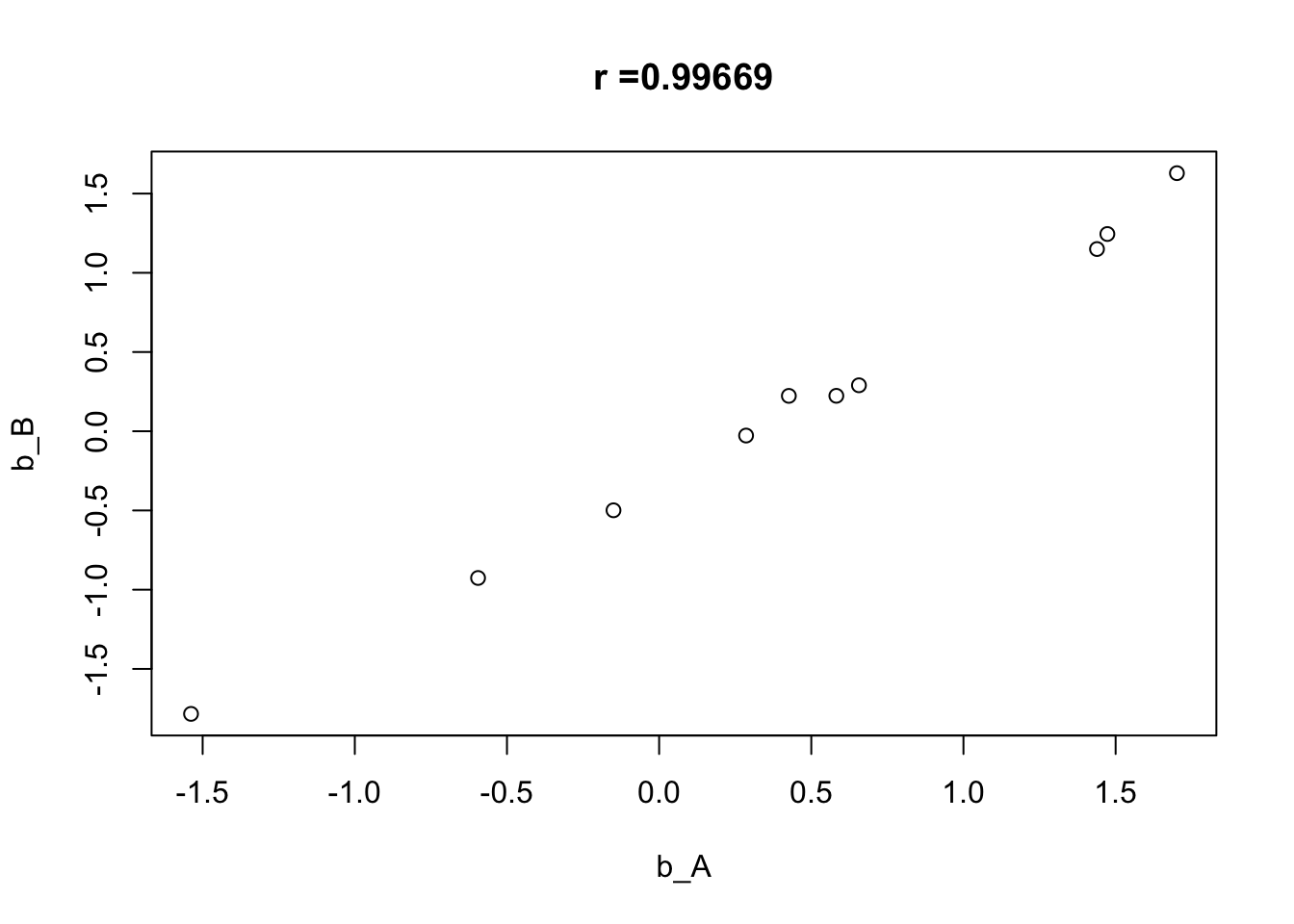
Rows: 5,000
Columns: 64
$ X <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19,…
$ V1 <dbl> -0.79498, -0.05589, 0.62650, -1.26832, 0.74921, 1.00922, -0.19147,…
$ V2 <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA…
$ V3 <int> 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, …
$ V4 <int> 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, …
$ V5 <int> 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, …
$ V6 <int> 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, …
$ V7 <int> 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, …
$ V8 <int> 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, …
$ V9 <int> 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, …
$ V10 <int> 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, …
$ V11 <int> 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, …
$ V12 <int> 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, …
$ V13 <int> 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, …
$ V14 <int> 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, …
$ V15 <int> 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, …
$ V16 <int> 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, …
$ V17 <int> 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ V18 <int> 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, …
$ V19 <int> 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, …
$ V20 <int> 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, …
$ V21 <int> 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ V22 <int> 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, …
$ V23 <int> 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, …
$ V24 <int> 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, …
$ V25 <int> 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
$ V26 <int> 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, …
$ V27 <int> 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, …
$ V28 <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, …
$ V29 <int> 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, …
$ V30 <int> 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, …
$ V31 <int> 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, …
$ V32 <int> 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, …
$ V33 <int> 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, …
$ V34 <int> 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, …
$ V35 <int> 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, …
$ V36 <int> 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, …
$ V37 <int> 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, …
$ V38 <int> 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, …
$ V39 <int> 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, …
$ V40 <int> 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, …
$ V41 <int> 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, …
$ V42 <int> 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, …
$ V43 <int> 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, …
$ V44 <int> 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, …
$ V45 <int> 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, …
$ V46 <int> 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, …
$ V47 <int> 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, …
$ V48 <int> 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, …
$ V49 <int> 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, …
$ V50 <int> 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, …
$ V51 <int> 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, …
$ V52 <int> 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, …
$ V53 <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA…
$ V54 <int> 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, …
$ V55 <int> 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, …
$ V56 <int> 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, …
$ V57 <int> 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, …
$ V58 <int> 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, …
$ V59 <int> 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, …
$ V60 <int> 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, …
$ V61 <int> 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, …
$ V62 <int> 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, …
$ V63 <int> 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, …