Lecture 11: Repeated Measure ANOVA

Overview of Lecture 11

1. Disadvantages and Advantages of Repeated Measure ANOVA
2. Repeated-measure ANOVA:
   • Random components (What to report)
   • Hypothesis testing
   • Assumptions for RM ANOVA

Question: How about the research scenario when more than two independent variables?

1.1 More independent variables

• When we want to add more independent variables to ANOVA-design,
  1. Blocking Design: 1 independent variable, 1 blocking variable
  2. Factorial Design: N-way ANOVA (e.g., 2-way ANOVA = 2 independent variables)
  3. Repeated Measures ANOVA: 1 independent variable measured only one time, and 1 independent variable measured repeated time points
  4. ANCOVA: 1 independent variable, and 1 covariate (continuous IV!)
  5. Mixed Design

Note. All ANOVA-related designs talked about in this class can handle only one dependent variable; if you want to deal with more than 2 dependent variable, we may consider other research designs…

1.2 Procedure of RM ANOVA

• To conduct the hypothesis test, we follow:

  1. Set the null hypothesis, and the alternative hypothesis
  2. Determine alpha level, and calculate dfs → critical value of test statistics
  3. Calculate the observed value of test statistics
  4. Make the statistical conclusion → (1) critical vs. observed, OR (2) 𝛼 vs. p
  5. Make the research conclusion → research question?

• Before conducting the hypothesis test, we check:

  1. Independence of observations → !!!ANOVA it NOT robust to violation of this!!!
  2. Normality → ANOVA tends to be relatively robust to non-normality.
  3. Homogeneity of variance → ANOVA can handle the violation of HOV when the group sizes are equal (i.e., balanced) and the group sizes are large enough. Or we can use Welch’s.

• Independence of the observations:

  1. Measurements from one case in the study are independent of other cases in the study.
  2. If we violate this assumption, we have to do something else!
  • → One of the remedies would be to use “Repeated Measures ANOVA (RM ANOVA)”

1.3 What Is RM ANOVA

• When multiple, repeat measurements are made on an experimental unit:
  • The observations can no longer be assumed to be independent.
    • → Result: Correlations in the residual errors among time periods!
    • → The correlations indicate the shared part among the individuals.
  • Not just over time, many other scenarios can result in repeated measures:
    • → Ex: Cross-over design where the treatments themselves are switched on the same experimental unit during the course of the experiment.
    • → In a cross-over design: each person goes through each treatment condition.
    • → Repeated measures are frequently encountered in clinical trials, development of growth models, and situations in which experimental units are difficult to acquire.

1.4 RM ANOVA Design

Source: https://explorable.com/repeated-measures-design

1.5 First Type of RM ANOVA: Repeated Measure Design

• Two types of repeated measures are common:
  1. Repeated measures in time: individuals receive a treatment, and then are followed with repeated measures on the response variable over several times.
     • Ex: The dataset might be:
       • For example, Sally is only in the “None” group. She never receives the “daily tutoring” condition.
       • Chi is only in the “daily tutoring” condition.
       • IV: “Tutoring type” can only explain the between-subject variance.

Tutoring Type	Time 1 (1st week out)	Time 2 (2nd week out)	Time 3 (3rd week out)
None	Sally Joe Montes	Sally Joe Montes	Sally Joe Montes
Once/week	Omar Fred Jenny	Omar Fred Jenny	Omar Fred Jenny
Daily	Chi Lena Caroline	Chi Lena Caroline	Chi Lena Caroline

1.6 Second Type of RM ANOVA: Cross-Over Design

• Two types of repeated measures are common:

  2. Cross-over Design: alternatively, experiments can involve administering all treatment levels (in a sequence) to each experimental unit.
  • Require a wash-out period between treatment applications to prevent (or minimize) carry-over effects.
    • Carry-over effects occur when the application of one treatment affects the response of the next treatment applied in the cross-over design.
  • The order of treatment administration in a crossover experiment is called a “sequence.”
    • The sequences should be determined a priori and the experimental units are randomized to sequences.
  • Time of a treatment administration is called a “period.”
    • Treatments are designated with capital letters, such as A, B, etc.
  • The most popular crossover design is the 2-sequence, 2-period, 2-treatment crossover design, with sequences AB and BA.
    • Often called the 2 × 2 crossover design.

1.7 Cross-Over Design: 2 x 2

2. Cross-over Design: alternatively, experiments can involve administering all treatment levels (in a sequence) to each experimental unit.

   • 2 × 2 crossover design:
     • Experimental units that are randomized to the AB sequence receive treatment A in the first period and treatment B in the second period.
     • Experimental units that are randomized to the BA sequence receive treatment B in the first period and treatment A in the second period.

   	Period 1	Period 2
   Sequence AB	A	B
   Sequence BA	B	A

Important

How many potential sequences are for J x J design?

$$\prod (J, J-1, \cdots,1)$$

1.8 Cross-Over Design: 3 x 3

• Two types of repeated measures are common:

  2. Cross-over Design: alternatively, experiments can involve administering all treatment levels (in a sequence) to each experimental unit.
  • ✔ 3 × 3 crossover design:
    • ✔ Consider a 3-treatment, 3-period design
      
    • ✔ A = no tutoring, B = once/week, C = daily

	Period 1	Period 2	Period 3
Sequence ABC	A	B	C
Sequence BCA	B	C	A
Sequence CAB	C	A	B
Sequence ACB	A	C	B
Sequence BAC	B	A	C
Sequence CBA	C	B	A

1.9 Carryover Effects Issues

Carryover effects:

• In a cross-over design, carryover effects refer to the residual effects of a treatment that persist and influence responses in subsequent treatment periods.

• Since each participant receives multiple treatments in sequence, the outcome measured in a later period may be affected not only by the current treatment but also by the lingering influence of prior treatments.

• ✔ Example:

  • One student was measured three math tests (Math A/B/C). Math A and B has overlapping items with similar difficulty.
  • Consider a 3×3 crossover design where a subject receives treatments A, B, and C across three periods.
    • If the subject receives treatment B in Period 1 and treatment A in Period 2, the effect observed in Period 2 may not reflect the pure effect of A—it may be contaminated by the residual effect of B, thus biasing the estimation of treatment A’s effectiveness.

• Discussion: Can you think about more carryover effect in your research area?

1.10 Problems of Carryover

• ✔ Main disadvantage: carryover effects may be confounded with treatment effects, because these effects cannot be estimated separately.
  • ✔ Think about Sequence BCA: You think you are estimating the effect of treatment A, but there is also a bias (or carryover) from the previous treatments to account for.
• ✔ Carryover effects can also bias the interpretation of data analysis, so an investigator should proceed cautiously when implementing a crossover design.
  • ✔ So, what do we do? Washout periods can diminish the impact of carryover effects
  • ➔ Washout period: time between treatment periods.
• ✔ These are especially helpful in clinical trials: Instead of immediately stopping and then starting the new treatment, a period of time where the drug is washed out of the patient’s system is used.
  • ✔ Ex: educational tests ➔ Subjects may be affected permanently by what they learned during the first period.

1.11 RM ANOVA Factors

• As with any ANOVA, repeated measures ANOVA tests the equality of means.
  • But, the statistical approach might differ.
• Statistical Terminology:
  • When a dependent variable is measured repeatedly for all sampled, this set of conditions is called a within-subjects factor.
    • ✔ Time (or trial) is typically used as our within-subject factor.
    • ✔ Emotion over time is typically used as our within-subject factor.
    • ✔ Self-reported Status is typically used as our within-subject factor.
  • When a dependent variable is measured on independent groups of sample members, where each group is exposed to a different condition, the set of conditions is called a between-subjects factor.
    • ✔ In the previous example, tutoring type would be the between-subject factor.
    • ✔ We think of these as the IVs from our “usual” ANOVAs.
  • When an analysis has both within-subjects factors and between-subjects factors, and considers their interaction effect, it is called a mixed design. (We will talk about it later!)

1.12 RM ANOVA Logic

• The logic behind a repeated measures ANOVA is very similar to that of a between-subjects ANOVA.
• Recall that in a between-subjects ANOVA (i.e., the “usual” ANOVA), we partition the total variability into:
  • Model (i.e., between-groups variability; SS_Model)
  • Error (i.e., within-groups variability; SS_Error)

1.13 RM ANOVA Logic II

• In RM ANOVA design, within-group variability (SS_w) is used as the error variability (SS_Error).

  • That said, “Why subjects differ within the same group” is unexplained!

• The F-statistic is calculated as the ratio of MS_Model to MS_Error:

  Independent ANOVA:
  $$F = \frac{MS_b}{MS_w} = \frac{MS_b}{MS_{error}}$$

1.14 RM ANOVA Logic III

Important

“Why subjects differ within the same group (e.g., treatment/control groups)” can be explained in RM ANOVA!

• The advantage of a repeated measures ANOVA:

  • ✔ Within-group variability (SS_w) is the error variability (SS_error) in an independent (between-subjects) ANOVA.
    
  • ✔ But, in a repeated measures ANOVA we further partition this error term, reducing its size, and increasing power!

• A repeated measures ANOVA calculates an F-statistic in a similar way:

  • Repeated Measures ANOVA: $F = \frac{MS_{conditions}}{MS_{error}}$

Generated by https://www.mermaidchart.com/app/projects

1.15 RM ANOVA Logic IV

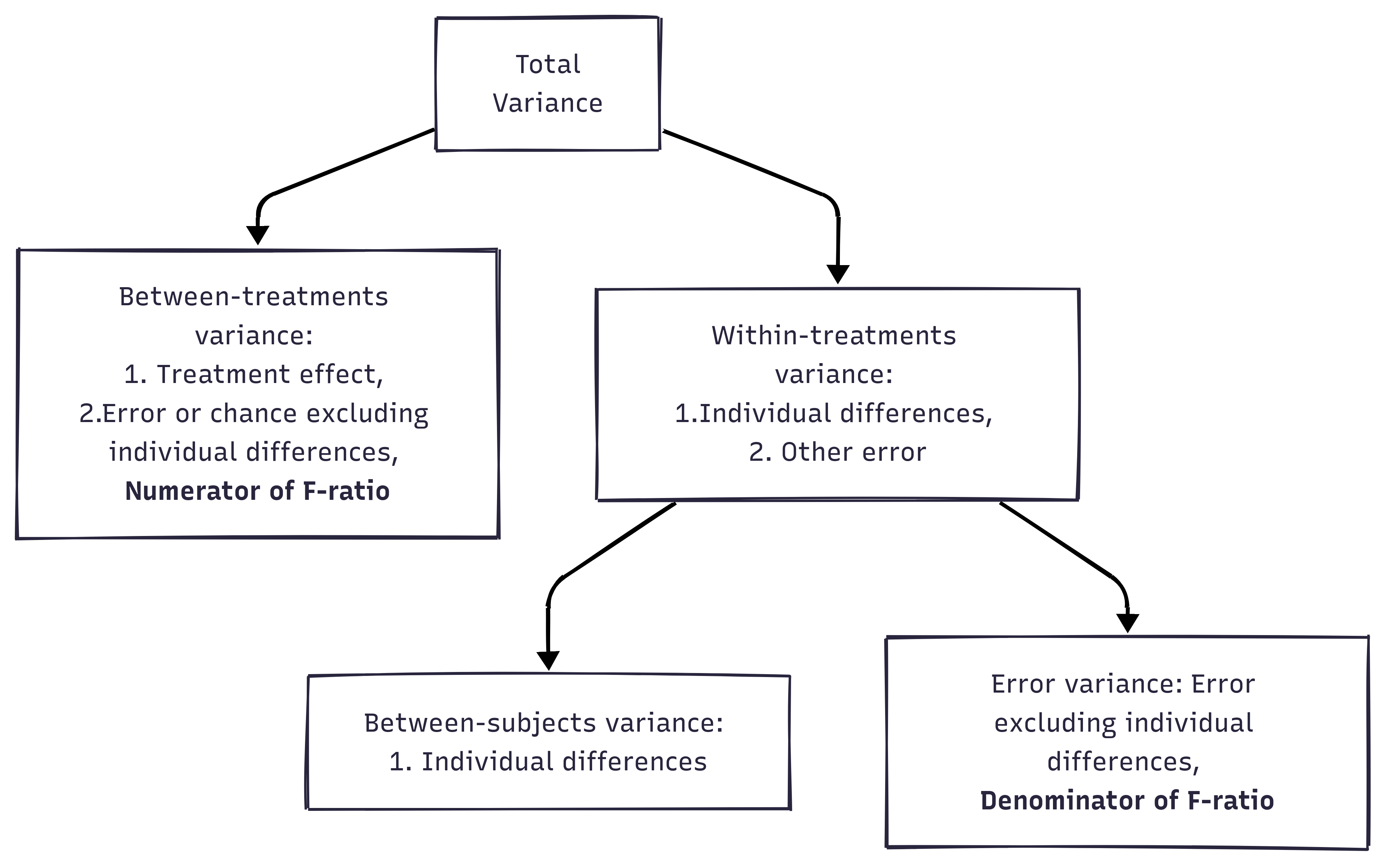
• Mathematically, we are partitioning the variability attributable to the differences between groups (SS_conditions) and variability within groups (SS_w) exactly as we do in a between-subjects (independent) ANOVA.

• With a repeated measures ANOVA, we are using the same subjects in each group, so we can remove the variability due to the individual differences between subjects, referred to as SS_subjects, from the within-groups variability (SS_w).

• We simply treat each subject as a “block.”

  • ✔ Each subject becomes a level of a factor, called subjects.
  • ✔ Then, we do not care about the interaction between within- and between-subjects.

• The ability to subtract SS_subjects will leave us with a smaller SS_error term:

  Independent ANOVA: $SS_{error} = SS_{w}$

  Repeated Measures ANOVA: $SS_{error} = SS_{w} - SS_{subjects}$

1.16 Example #1

• Researchers are interested in the effect of drug on blood concentration of histamine at 0, 1, 3, and 5 minutes after injection of the drug.
  • Subjects: dogs
  • ✔ DV: blood concentration of histamine
  • ✔ Within-subject factor: time (4 levels: 0, 1, 3, and 5 minutes)
• Six dogs, four time points

Dog ID	time1	time2	time3	time4	Dog mean
1	10	16	25	26	19.25
2	12	19	27	25	20.75
3	13	20	28	28	22.25
4	12	18	25	15	17.50
5	11	20	26	18	18.75
6	10	22	27	19	19.50
Time mean	11.33	19.17	26.33	21.83	Grand mean = 19.67

1.17 Table for RM ANOVA Report

🔴 ANOVA Table of Repeated Measures ANOVA

Source	Sub-Component	SS	df	MS	F
Between-time
Within-time (I)	Between-Subjects
Within-time (II)	Within-Subjects / Error

Note. Under the repeated measures ANOVA, we can decompose the total variability:

Total variability of DV = “between-time” variability + “within-time” variability

• ➔ “Within-Time” variability = “Between-subjects” variability + “Within-subjects” variability
  
• ➔ “Within-Subjects” variability is treated as “error”
  • We know outcome differ because of time (consistent time variability over people) or people (consistent people variability over time), what left is unexplained

Between-subjects are useful because we can use it to explain the treatment effects / gender effects (anything relevant to why people different from each other).

---

1.17.1 Think about “between-time” row in ANOVA table

Statistics

We calculate mean square for between-time as:

$$MS_{btime} = \frac{SS_{btime}}{df_{btime}}$$

Where:

$$SS_{btime} = \sum n_{subjects}(\bar{Y}_{time} - \bar{Y}_{grand})^2 = 6(11.33 - 19.67)^2 + \cdots + 6(21.83 - 19.67)^2 = 712.961$$

$$df_{btime} = \text{Number of time points} - 1 = 4 - 1 = 3$$

Thus,

$$MS_{btime} = \frac{712.96}{3} = 237.65$$

Results

Data

Dog ID	time1	time2	time3	time4	Dog mean
1	10	16	25	26	19.25
2	12	19	27	25	20.75
3	13	20	28	28	22.25
4	12	18	25	15	17.50
5	11	20	26	18	18.75
6	10	22	27	19	19.50
Time means	11.33	19.17	26.33	21.83	Grand Mean = 19.67

ANOVA Table (Partial)

Source	SS	df	MS	F
Between-time	712.96	3	237.65
Within-time
Between-Subjects
Error

---

1.17.2 Think about “between-subjects” row in ANOVA table

Statistics

We calculate mean square for between-subjects (between-dog) as:

$$MS_{bsubjects} = \frac{SS_{bsubjects}}{df_{bsubjects}}$$

Where:

$$SS_{bsubjects} = \sum n_{times}(\bar{Y}_i - \bar{Y}_{grand})^2 = 4*(19.25 - 19.67)^2 + \cdots + 4*(19.50 - 19.67)^2 = 54.33$$

dog_means <- c(19.25, 20.75, 22.25, 17.50, 18.75, 19.50 )
sum(4 * (dog_means - 19.67)^2)

[1] 54.3336

$$df_{bsubject} = N_{dogs} - 1 = 6 - 1 = 5$$

Thus,

$$MS_{bsubjects} = \frac{54.33}{5} = 10.866$$

Results

Data

Dog ID	time1	time2	time3	time4	Dog mean
1	10	16	25	26	19.25
2	12	19	27	25	20.75
3	13	20	28	28	22.25
4	12	18	25	15	17.50
5	11	20	26	18	18.75
6	10	22	27	19	19.50
Time means	11.33	19.17	26.33	21.83	Grand Mean = 19.67

ANOVA Table (Partial)

Source	SS	df	MS	F
Between-time	712.96	3	237.65
Within-time
Between-Subjects	54.33	5	10.87
Error

---

1.17.3 Think about “within-time” row in ANOVA table

Statistics

We calculate the mean square for within-time as:

$$MS_{wtime} = \frac{SS_{wtime}}{df_{wtime}}$$

Where:

$$SS_{wtime} = \sum_{i,time}(y_{i,time} - \bar{Y}_{time})^2 = (10 - 11.33)^2 + \cdots + (19 - 21.83)^2 = 170.33$$

$$df_{wtime} = (6 - 1) + (6 - 1) + (6 - 1) + (6 - 1) = 20$$

Thus,

$$MS_{wtime} = \frac{170.33}{20} = 8.5165$$

Results

Data

Dog ID	time1	time2	time3	time4	Dog mean
1	10	16	25	26	19.25
2	12	19	27	25	20.75
3	13	20	28	28	22.25
4	12	18	25	15	17.50
5	11	20	26	18	18.75
6	10	22	27	19	19.50
Time means	11.33	19.17	26.33	21.83	Grand Mean = 19.67

ANOVA Table (Partial)

Source	SS	df	MS	F
Between-time	712.96	3	237.65
Within-time	170.33	20	8.52
Between-Subjects	54.33	5	10.87
Error

---

1.17.4 Think about “Error” row in ANOVA table

Statistics

We calculate the mean square for error as:

$$MS_{error} = \frac{SS_{error}}{df_{error}}$$

Where:

$$SS_{error} = SS_{wtime} - SS_{bsubjects} = 170.33 - 54.33 = 116$$

$$df_{error} = df_{wtime} - df_{bsubjects} = 20 - 5 = 15$$

Thus:

$$MS_{error} = \frac{116}{15} = 7.333$$

Results

Data

Dog ID	time1	time2	time3	time4	Dog mean
1	10	16	25	26	19.25
2	12	19	27	25	20.75
3	13	20	28	28	22.25
4	12	18	25	15	17.50
5	11	20	26	18	18.75
6	10	22	27	19	19.50
Time means	11.33	19.17	26.33	21.83	Grand Mean = 19.67

ANOVA Table (Complete)

Source	SS	df	MS	F
Between-time	712.96	3	237.65
Within-time	170.33	20	8.52
Between-Subjects	54.33	5	10.87
Error	116.00	15	7.33

1.18 Hypothesis Test Procedure

1.18.1 ✅ Main Effect of Time:

Research Question:
Does histamine concentration change over time?
(That is, does mean histamine concentration differ across the four time points?)

(Histamine is a chemical your immune system releases.)

Null Hypothesis:
$$H_0: \mu_{time1} = \mu_{time2} = \mu_{time3} = \mu_{time4}$$

ANOVA Table

Source	SS	df	MS	F
Between-time	712.96	3	237.65	237.65 / 7.33 = 30.73
Within-time	170.33	20	8.52	8.52 / 7.33 = 1.16
Between-Subjects	54.33	5	10.87	10.87 / 7.33 = 1.48
Error	116.00	15	7.33

Conclusion

• Under $\alpha = 0.05$, the critical value for $df_{time} = 3$ and $df_{error} = 15$ from the F-table is:
  $F_{crit} = 3.29$

• Since the observed F-value for the time effect is 30.73, which exceeds the critical value of 3.29:

  • ✅ We reject the null hypothesis.
  • ✅ There is a significant main effect of time.

Conclusion:
There is a significant difference in histamine concentration across the four time points.

1.19 Repeated Measures ANOVA: Assumption I

🔍 Before conducting the hypothesis test, we check:

1. Independence of observations
   ➔ !!! ANOVA is NOT robust to violation of this !!!

2. Normality
   ➔ ANOVA tends to be relatively robust to non-normality.

3. Homogeneity of variance (HOV)
   ➔ ANOVA can handle HOV violations when:

   • Group sizes are equal (i.e., balanced)
   • Group sizes are large enough
     ➔ Otherwise, consider using Welch’s ANOVA

✅ Independence of the Observations:

• ✔ Measurements from one case in the study are independent of other cases in the study.
• ✔ If we violate this assumption, we have to do something else!
  ➔ One remedy would be to use repeated measures ANOVA.

❓ Then, which assumption should we check for repeated measures ANOVA?

1.20 Repeated Measures ANOVA: Assumption II

1.20.1 🔍 Before conducting the hypothesis test, we check:

1. Independency
   ➔ Do not need to check! (in repeated measures designs)

2. Normality
   ➔ The dependent variable (DV) at each level of the independent variable(s) should be approximately normally distributed.
   ➔ However, ANOVA tends to be relatively robust to non-normality.

3. Instead of HOV (Homogeneity of Variance)
   ➔ We should check “Sphericity”

1.20.2 🧠 Sphericity

• The concept of sphericity is the repeated measures equivalent of homogeneity of variances.
• Sphericity is the condition where the variances of the differences between all combinations of related groups (levels) are equal.
• Violation of sphericity occurs when the variances of the differences between all combinations of related groups are not equal.
• Testing for sphericity
  • is an option in PROC GLM using Mauchly’s Test for Sphericity.
  • In R, testing for sphericity in a repeated measures ANOVA is typically conducted using the anova_test() function from the rstatix package, which includes Mauchly’s Test of Sphericity.

1.21 Sphericity Illustration

Table

Dog ID	time1	time2	time3	t1 - t2	t1 - t3	t2 - t3
1	10	16	25	-6	-15	-9
2	12	19	27	-7	-15	-8
3	13	20	28	-7	-15	-8
4	12	18	25	-6	-13	-7
5	11	20	26	-9	-15	-6
6	10	22	27	-12	-17	-5
Variance				5.367	1.6	2.167

Figure

library(tidyverse)
library(plotly)
dat_wide <- tribble(
  ~ID, ~T1, ~T2, ~T3,
  1, 10, 16, 25,
  2, 12, 19, 27,
  3, 13, 20, 28,
  4, 12, 18, 25,
  5, 11, 20, 26,
  6, 10, 22, 27
)
dat_long <- dat_wide |> 
  pivot_longer(starts_with("T"), names_to = "Time", values_to = "Y") |> 
  mutate(Time = factor(Time, levels = paste0("T",1:3)),
         ID = factor(ID, levels = 1:6)) 
dat_long |> 
  plot_ly(x=~Time, y=~Y) |> 
  add_markers(color=~ID) |> 
  add_lines(color=~ID)

This table presents:

• The raw time-point measurements (time1, time2, time3)
• Pairwise difference scores (t1 - t2, t1 - t3, t2 - t3)
• Variance of each set of pairwise differences at the bottom (used to assess sphericity)

We are concerned with these variances for “sphericity”

1.22 ✅ Step-by-step: Testing Sphericity in R

1. Prepare your data

You need your data in long format: one row per subject per time point.

Example:

library(rstatix)
library(tidyverse)
# Sample wide-format data
head(dat_long)

# A tibble: 6 × 3
  ID    Time      Y
  <fct> <fct> <dbl>
1 1     T1       10
2 1     T2       16
3 1     T3       25
4 2     T1       12
5 2     T2       19
6 2     T3       27

2. Run repeated measures ANOVA with sphericity test

anova_results <- dat_long %>%
  anova_test(dv = Y, wid = ID, within = Time)

anova_results

ANOVA Table (type III tests)

$ANOVA
  Effect DFn DFd       F       p p<.05  ges
1   Time   2  10 221.861 5.2e-09     * 0.95

$`Mauchly's Test for Sphericity`
  Effect     W     p p<.05
1   Time 0.407 0.165      

$`Sphericity Corrections`
  Effect   GGe     DF[GG]   p[GG] p[GG]<.05   HFe     DF[HF]    p[HF] p[HF]<.05
1   Time 0.628 1.26, 6.28 2.8e-06         * 0.739 1.48, 7.39 4.28e-07         *

• This will output:

  1. ANOVA table
  2. Mauchly’s Test of Sphericity
  3. Greenhouse-Geisser and Huynh-Feldt corrections (if sphericity is violated)

3. View the sphericity test

anova_results$`Mauchly's Test for Sphericity`

  Effect     W     p p<.05
1   Time 0.407 0.165      

anova_results$`Sphericity Corrections`

  Effect   GGe     DF[GG]   p[GG] p[GG]<.05   HFe     DF[HF]    p[HF] p[HF]<.05
1   Time 0.628 1.26, 6.28 2.8e-06         * 0.739 1.48, 7.39 4.28e-07         *

📌 Interpreting the Output

Test	Interpretation
Mauchly’s Test (p > .05)	Sphericity holds – use standard F-statistic
Mauchly’s Test (p < .05)	Sphericity violated – use corrected F-statistics

If violated, refer to the corrected tests:

• Use Greenhouse-Geisser correction unless epsilon > 0.75
• Otherwise, Huynh-Feldt is often preferred

📝 Example Reporting

Mauchly’s test indicated that the assumption of sphericity had not been violated, W = 0.407, p = .165. We can use standard F-test.

1.23 📌 Report Between-Subject Variability (Random effects)

The anova_test() function in the rstatix package does not provide between-subject variability directly in its output. This is because anova_test() focuses on the within-subject effects (repeated measures factors) and treats subject as a blocking factor rather than estimating its variance as a separate effect.

In traditional repeated measures ANOVA, between-subject variability corresponds to:

The variance between the subjects’ overall means — captured by the SS_subjects term.

However, in the anova_test() framework: - The subject-level variability is partialed out (i.e., controlled for), not estimated explicitly. - It is absorbed into the model as the random effect (like a blocking factor in a randomized block design).

---

1.23.1 ✅ Workaround: Manually Compute Between-Subject SS

Formula again:

You can compute the between-subject sum of squares manually from the subject means using the formula:

$$SS_{\text{subjects}} = k \sum (\bar{Y}_i - \bar{Y}_{\text{grand}})^2$$

Where:

• $\bar{Y}_i$: subject means across time points
• $\bar{Y}_{\text{grand}}$: grand mean
• $k$: number of repeated measurements (e.g., 4 time points)

Example in R:

# Compute subject means and grand mean
subject_means <- dat_long %>%
  group_by(ID) %>%
  summarise(subject_mean = mean(Y))

grand_mean <- mean(subject_means$subject_mean)

# Number of repeated measures (e.g., 4 time points)
k <- n_distinct(dat_long$Time)

# Compute SS_subjects
SS_subjects <- subject_means %>%
  summarise(SS = k * sum((subject_mean - grand_mean)^2)) %>%
  pull(SS)

SS_subjects

[1] 20.27778

This gives the between-subjects sum of squares.

📌 Summary

Component	Available from anova_test()	How to Obtain
Within-subjects	✅ Effect == "Residuals"	filter(Effect == "Residuals")
Between-subjects	❌ Not provided	✅ Compute manually using subject means

Fin