---
title: "Lecture 10: Two-way ANOVA II"
subtitle: "Statistics in 2-way ANOVA"
date: "2025-03-07"
date-modified: "`{r} Sys.Date()`"
execute:
eval: true
echo: true
warning: false
message: false
webr:
editor-font-scale: 1.2
format:
html:
toc-expand: 3
code-tools: true
code-line-numbers: false
code-fold: false
code-summary: "Click to see R code"
number-offset: 1
fig.width: 10
fig-align: center
message: false
grid:
sidebar-width: 350px
uark-revealjs:
chalkboard: true
embed-resources: false
code-fold: false
number-sections: true
number-depth: 1
footer: "ESRM 64503"
slide-number: c/t
tbl-colwidths: auto
scrollable: true
output-file: slides-index.html
mermaid:
theme: forest
---
::: objectives
## Overview of Lecture 09 & Lecture 10 {.unnumbered}
1. The rest of the semester
2. Advantage of Factorial Design
3. Two-way ANOVA:
- Steps for conducting 2-way ANOVA
- Hypothesis testing
- Assumptions for 2-way ANOVA
- Visualization
- Difference between 1-way and 2-way ANOVA
**Question**: How about the research scenario when more than two independent variables?
:::
# Hypothesis testing for two-way ANOVA
## Hypothesis testing for two-way ANOVA (I)
- For two-way ANOVA, there are three distinct hypothesis tests :
- Main effect of Factor A
- Main effect of Factor B
- Interaction of A and B
::: callout-note
### Definition
F-test
: Three separate F-tests are conducted for each!
Main effect
: Occurs when there is a difference between levels for one factor
Interaction
: Occurs when the effect of one factor on the DV depends on the particular level of the other factor
: Said another way, when the difference in one factor is moderated by the other
: Said a third way, if the difference between levels of one factor is different, depending on the other factor
:::
## Hypothesis testing for two-way ANOVA (II)
1. Hypothesis test for the main effect with more than 2 levels
- Mean differences among levels of one factor:
i) Differences are tested for statistical significance
ii) Each factor is evaluated independently of the other factor(s) in the study
- Factor A’s Main effect: “Controlling Factor B, are there differences in the DV across Factor A?”
$H_0$: $\mu_{A_1}=\mu_{A_2}=\cdots=\mu_{A_k}$
$H_1$: At least one $\mu_{A_i}$ is different from the control group in Factor A
- Factor B’s Main effect : “Controlling Factor A, are there differences in the DV across Factor B?”
$H_0$: $\mu_{B_1}=\mu_{B_2}=\cdots=\mu_{B_k}$
$H_1$: At least one $\mu_{B_i}$ is different from the control group in Factor A
- Interaction effect between A and B:
$H_0:\mu_{A_1B_2}-\mu_{A_1B_1}=\mu_{A_2B_2}-\mu_{A_2B_1}$
or $H_0: \mu_{A_1B_1}-\mu_{A_2B_1}=\mu_{A_1B_2}-\mu_{A_2B_2}$
::: rmdnote
B's group differences do not change at different levels of A. OR A's group differences do not change at different levels of B.
:::
## Hypothesis testing for two-way ANOVA (III)
::: callout-important
## Example
**Background**: A researcher is investigating how study method (Factor A: Lecture vs. Interactive) and test format (Factor B: Multiple-Choice vs. Open-Ended) affect student performance (dependent variable: test scores). The study involves randomly assigning students to one of the two study methods and then assessing their performance on one of the two test formats.
- **Main Effect of Study Method (Factor A):**
- [H0:]{style="color:royalblue; font-weight:bold"} There is no difference in test scores between students who used the Lecture method and those who used the Interactive method.
- [H1:]{style="color:tomato; font-weight:bold"} There is a significant difference in test scores between the two study methods.
- **Main Effect of Test Format (Factor B):**
- [H0:]{style="color:royalblue; font-weight:bold"} There is no difference in test scores between students taking a Multiple-Choice test and those taking an Open-Ended test.
- [H1:]{style="color:tomato; font-weight:bold"} There is a significant difference in test scores between the two test formats.
- **Interaction Effect (Study Method × Test Format):**
- [H0:]{style="color:royalblue; font-weight:bold"} The effect of study method on test scores is the same regardless of test format.
- [H1:]{style="color:tomato; font-weight:bold"} The effect of study method on test scores depends on the test format (i.e., there is an interaction).
:::
## Hypothesis testing for two-way ANOVA (IV)
::: callout-note
### Example: Tutoring Program and Types of Schools on Grades
- **IVs**:
1. Tutoring Programs: (1) No tutor; (2) Once a week; (3) Daily
2. Types of schools: (1) Public (2) Private-secular (3) Private-religious
- **Research purpose**: to examine the effect of tutoring program (no tutor, once a week, and daily) AND types of school (e.g., public, private-secular, and private-religious) on the students’ grades
- **Question**: What are the null and alternative hypotheses for the main effects in the example?:
- Factor A’s Main effect: “[Controlling school types, are there differences in the students’ grade across three tutoring programs?]{.mohu}”
$H_0$: $\mu_{\mathrm{no\ tutor}}=\mu_{\mathrm{once\ a\ week}}=\mu_{\mathrm{daily}}$
- Factor B’s Main effect : “[Controlling tutoring programs, are there differences in the students’ grades across three school types?]{.mohu}”
$H_0$: $\mu_{\mathrm{public}}=\mu_{\mathrm{private-religious}}=\mu_{\mathrm{private-secular}}$
:::
## Model 1: Two-Way ANOVA without interaction
- The main-effect only ANOVA with no interaction has a following statistical form:
$$
\mathrm{Grade} = \beta_0 + \beta_1 \mathrm{Toturing_{Once}} + \beta_2 \mathrm{Toturing_{Daily}} \\ + \beta_3 \mathrm{SchoolType_{PvtS}} + \beta_4 \mathrm{SchoolType_{PvtR}}
$$
```{webr-r}
#| context: setup
library(tidyverse)
# Set seed for reproducibility
set.seed(123)
# Define sample size per group
n <- 30
# Define factor levels
tutoring <- rep(c("No Tutor", "Once a Week", "Daily"), each = 3 * n)
school <- rep(c("Public", "Private-Secular", "Private-Religious"), times = n * 3)
# Simulate student grades with assumed effects
grades <- c(
rnorm(n, mean = 75, sd = 5), # No tutor, Public
rnorm(n, mean = 78, sd = 5), # No tutor, Private-Secular
rnorm(n, mean = 76, sd = 5), # No tutor, Private-Religious
rnorm(n, mean = 80, sd = 5), # Once a week, Public
rnorm(n, mean = 83, sd = 5), # Once a week, Private-Secular
rnorm(n, mean = 81, sd = 5), # Once a week, Private-Religious
rnorm(n, mean = 85, sd = 5), # Daily, Public
rnorm(n, mean = 88, sd = 5), # Daily, Private-Secular
rnorm(n, mean = 86, sd = 5) # Daily, Private-Religious
)
# Create a data_frame
data <- data.frame(
Tutoring = factor(tutoring, levels = c("No Tutor", "Once a Week", "Daily")),
School = factor(school, levels = c("Public", "Private-Secular", "Private-Religious")),
Grades = grades
)
```
```{r}
#| eval: true
#| code-fold: true
#| code-summary: "Data Generation"
library(tidyverse)
# Set seed for reproducibility
set.seed(123)
# Define sample size per group
n <- 30
# Define factor levels
tutoring <- rep(c("No Tutor", "Once a Week", "Daily"), each = 3 * n)
school <- rep(c("Public", "Private-Secular", "Private-Religious"), times = n * 3)
# Simulate student grades with assumed effects
grades <- c(
rnorm(n, mean = 75, sd = 5), # No tutor, Public
rnorm(n, mean = 78, sd = 5), # No tutor, Private-Secular
rnorm(n, mean = 76, sd = 5), # No tutor, Private-Religious
rnorm(n, mean = 80, sd = 5), # Once a week, Public
rnorm(n, mean = 83, sd = 5), # Once a week, Private-Secular
rnorm(n, mean = 81, sd = 5), # Once a week, Private-Religious
rnorm(n, mean = 85, sd = 5), # Daily, Public
rnorm(n, mean = 88, sd = 5), # Daily, Private-Secular
rnorm(n, mean = 86, sd = 5) # Daily, Private-Religious
)
# Create a dataframe
data <- data.frame(
Tutoring = factor(tutoring, levels = c("No Tutor", "Once a Week", "Daily")),
School = factor(school, levels = c("Public", "Private-Secular", "Private-Religious")),
Grades = grades
)
```
- Main effect of Tutoring Programs
- Collapsing across School Type
- Ignoring the difference levels of School Type
- Averaging DV regarding Tutoring Programs across the levels of School Type
- Main effect of School Type
- Collapsing across Tutoring Program
- Ignoring the difference levels of Tutoring Program
- Averaging DV regarding School Type across the levels of Tutoring Programs
------------------------------------------------------------------------
::: panel-tabset
### R Plot
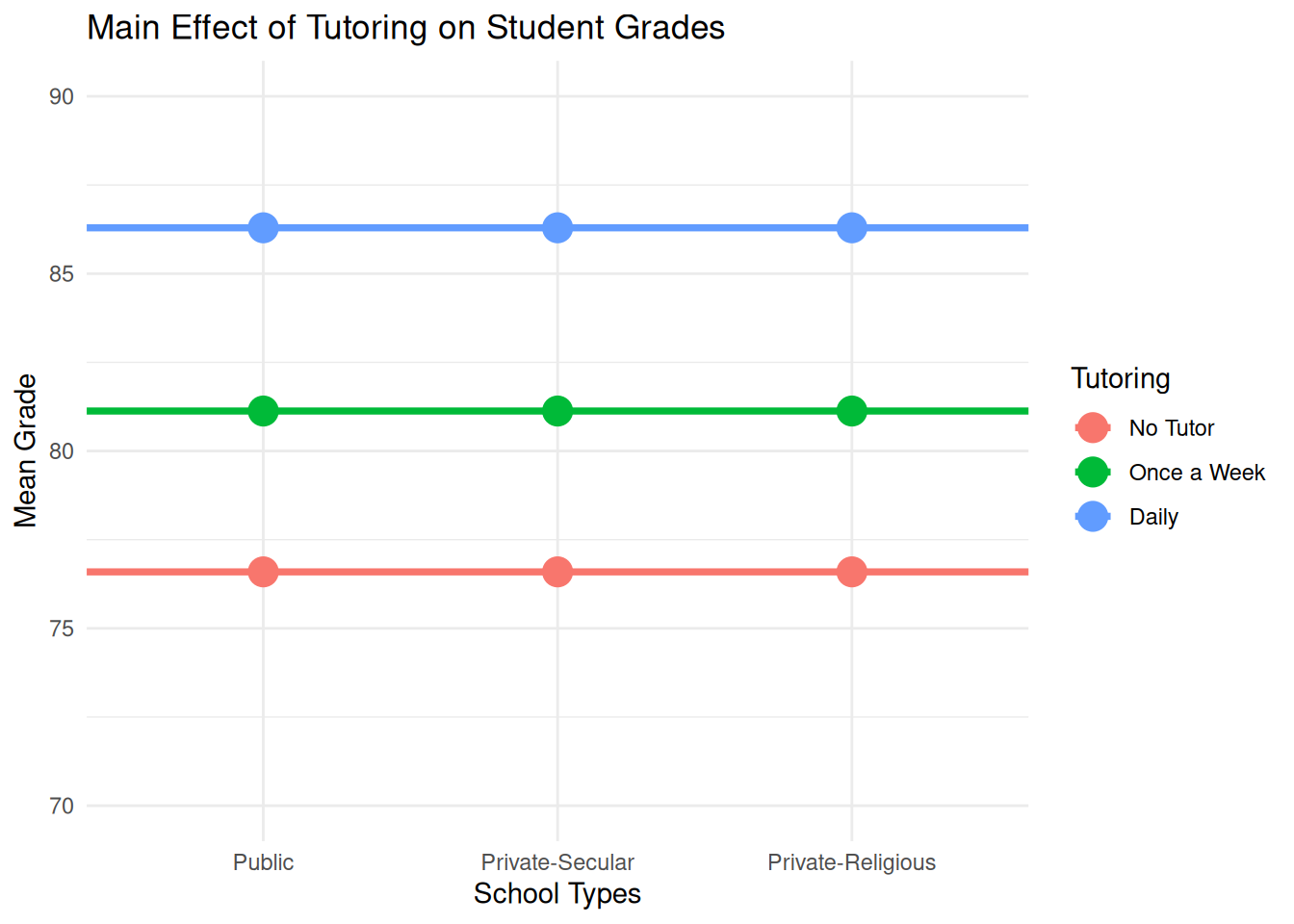
Ignoring the effect of school types, we can tell the main effect of tutor programs on students' grades (Daily tutoring has the highest grade, followed by *once a week*).
```{r}
#| code-fold: true
# Compute mean and standard error for each tutoring group
tutoring_summary <- data |>
group_by(Tutoring) |>
summarise(
Mean_Grade_byTutor = mean(Grades),
School = factor(c("Public","Private-Secular", "Private-Religious"),
levels = c("Public","Private-Secular", "Private-Religious"))
)
school_summary <- data |>
group_by(School) |>
summarise(
Mean_Grade_bySchool = mean(Grades)
)
total_summary <- tutoring_summary |>
left_join(school_summary, by = "School")
# Plot main effect of tutoring
ggplot(total_summary, aes(x = School)) +
geom_point(aes(y = Mean_Grade_byTutor, color = Tutoring), size = 5) +
geom_hline(aes(yintercept = Mean_Grade_byTutor, color = Tutoring), linewidth = 1.3) +
scale_y_continuous(limits = c(70, 90), breaks = seq(70, 90, 5)) +
labs(title = "Main Effect of Tutoring on Student Grades",
x = "School Types",
y = "Mean Grade") +
theme_minimal()
```
### Summary Statistics
```{r}
distinct(tutoring_summary[, c("Tutoring", "Mean_Grade_byTutor")])
```
### Interpretation of the Plot
- The x-axis represents three school types.
- The y-axis represents the mean student grades for the different tutoring programs: No Tutor, Once a Week, and Daily.
- If the main effect of tutoring is significant, we expect to see noticeable differences in mean grades across tutoring conditions.
:::
## You turn: Visualize Main Effect of School Type
::: panel-tabset
### Marginal Means for each tutoring / school type group
```{webr-r}
School_Levels <- c("Public",
"Private-Secular",
"Private-Religious")
## Calculate marginal means for tutoring
tutoring_summary <- data |>
group_by(Tutoring) |>
summarise(
Mean_Grade_byTutor = mean(Grades),
School = factor(School_Levels,
levels = School_Levels)
)
## Calculate marginal means for school types
school_summary <- data |>
group_by(School) |>
summarise(
Mean_Grade_bySchool = mean(Grades)
)
## Combine them into one table
total_summary <- tutoring_summary |>
left_join(school_summary, by = "School")
```
### Plot main effect of School Type
```{webr-r}
ggplot(total_summary, aes(x = Tutoring)) +
geom_point(aes(y = Mean_Grade_bySchool, color = School)) +
geom_hline(aes(yintercept = Mean_Grade_bySchool, color = School), linewidth = 1.3) +
scale_y_continuous(limits = c(70, 90), breaks = seq(70, 90, 5)) +
labs(title = "Main Effect of School Type on Student Grades",
x = "Tutoring Type",
y = "Mean Grade") +
theme_minimal() +
theme(legend.position = "none") # Remove legend for cleaner visualization
```
:::
## Combined Visualization for no-interaction model
::: panel-tabset
### R Plot
```{webr-r}
fit <- lm(Grades ~ Tutoring + School, data = data)
Line_No_Tutor <- c(fit$coefficients[1], fit$coefficients[1] + c(fit$coefficients[4], fit$coefficients[5]))
Line_Once_A_Week <- Line_No_Tutor + fit$coefficients[2]
Line_Daily <- Line_No_Tutor + fit$coefficients[3]
School_Levels <- c("Public","Private-Secular", "Private-Religious")
combined_vis_data <- data.frame(
School_Levels,
Line_No_Tutor,
Line_Once_A_Week,
Line_Daily
)
ggplot(data = combined_vis_data, aes(x = School_Levels)) +
geom_path(aes(y = as.numeric(Line_No_Tutor)), group = 1, color = "red", linewidth = 1.4) +
geom_path(aes(y = as.numeric(Line_Once_A_Week)), group = 1, color = "green", linewidth = 1.4) +
geom_path(aes(y = as.numeric(Line_Daily)), group = 1, color = "blue", linewidth = 1.4) +
geom_point(aes(y = as.numeric(Line_No_Tutor))) +
geom_point(aes(y = as.numeric(Line_Once_A_Week))) +
geom_point(aes(y = as.numeric(Line_Daily))) +
labs(title = "Main Effect of Tutoring and School Type on Student Grades",
x = "Tutoring Type",
y = "Mean Grade") +
theme_minimal() +
theme(legend.position = "none")
```
### In the graph
- There is the LARGE effect of Factor [Tutoring]{.mohu} and very small effect of [School Type]{.mohu}:
- Effect of Factor [Tutoring]{.mohu}: the LARGE vertical distance
- Effect of Factor [School Type]{.mohu}: the very small horizontal distance
:::
## Real-World Examples of Interaction Effects
::: panel-tabset
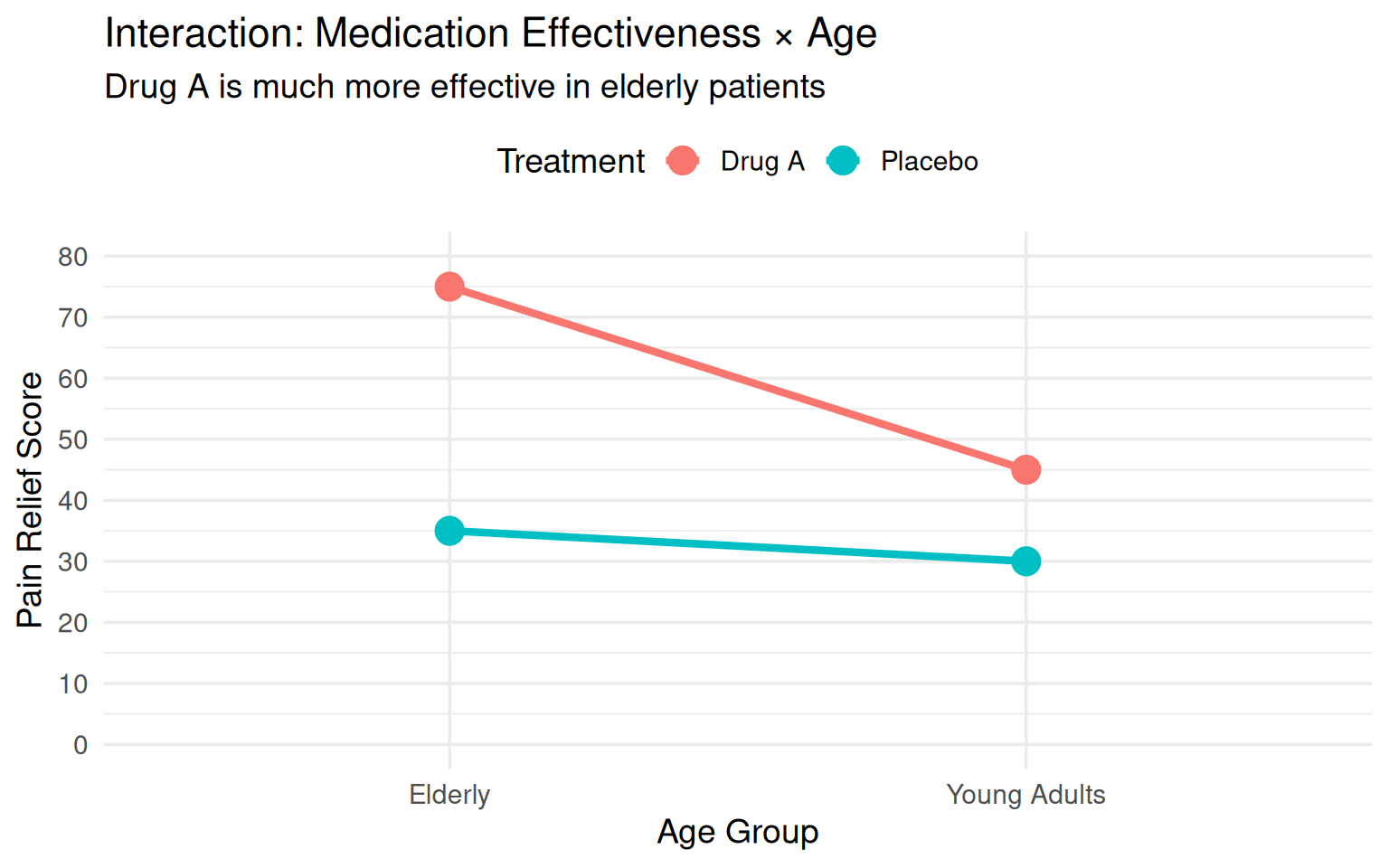
#### Example 1: Medication & Age
**Research Question**: Does the effectiveness of a new pain medication depend on patient age?
**Factors:**
- Factor A: Medication Type (Drug A vs. Placebo)
- Factor B: Age Group (Young Adults vs. Elderly)
**Observed Pattern (Interaction Present):**
- **Young Adults**: Drug A shows moderate improvement over placebo (Δ = 15 points)
- **Elderly**: Drug A shows LARGE improvement over placebo (Δ = 40 points)
**Why the interaction?**
- Elderly patients may have different metabolism rates
- Age-related changes in pain receptors may make them more responsive to the drug
- Elderly may have more severe baseline pain, allowing more room for improvement
**Implication**: You cannot simply say "Drug A works" - you must specify "Drug A works **especially well** for elderly patients"
**Visualization:**
```{r}
#| echo: false
#| fig-width: 8
#| fig-height: 5
library(ggplot2)
medication_data <- data.frame(
Age = rep(c("Young Adults", "Elderly"), each = 2),
Treatment = rep(c("Placebo", "Drug A"), 2),
Pain_Relief = c(30, 45, 35, 75)
)
ggplot(medication_data, aes(x = Age, y = Pain_Relief, color = Treatment, group = Treatment)) +
geom_point(size = 5) +
geom_line(linewidth = 1.5) +
labs(title = "Interaction: Medication Effectiveness × Age",
subtitle = "Drug A is much more effective in elderly patients",
x = "Age Group",
y = "Pain Relief Score",
color = "Treatment") +
theme_minimal(base_size = 14) +
scale_y_continuous(limits = c(0, 80), breaks = seq(0, 80, 10)) +
theme(legend.position = "top")
```
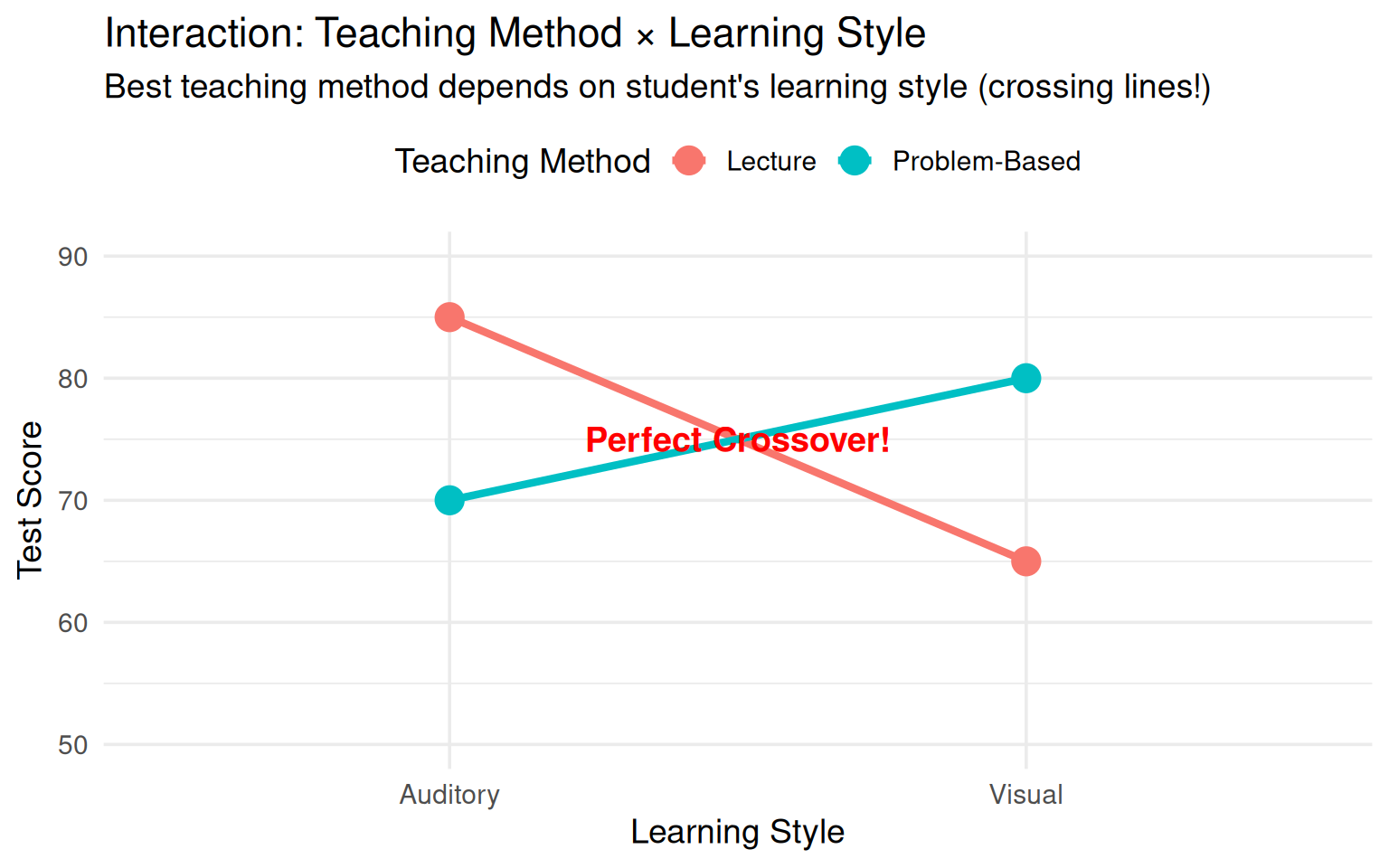
#### Example 2: Teaching Method & Learning Style
**Research Question**: Does the best teaching method depend on students' learning style?
**Factors:**
- Factor A: Teaching Method (Lecture-Based vs. Problem-Based Learning)
- Factor B: Learning Style (Visual vs. Auditory Learners)
**Observed Pattern (Interaction Present):**
- **Visual Learners**: Problem-Based Learning >> Lecture-Based (80 vs. 65)
- **Auditory Learners**: Lecture-Based >> Problem-Based Learning (85 vs. 70)
**Why the interaction?**
- Visual learners benefit from hands-on activities with diagrams and visual aids in PBL
- Auditory learners benefit from verbal explanations and discussions in lectures
- One-size-fits-all teaching ignores individual differences in cognitive processing
**Implication**: Educational policy should consider **matching** teaching methods to learning styles, not universally adopting one method.
**Visualization:**
```{r}
#| echo: false
#| fig-width: 8
#| fig-height: 5
teaching_data <- data.frame(
Learning_Style = rep(c("Visual", "Auditory"), each = 2),
Method = rep(c("Lecture", "Problem-Based"), 2),
Test_Score = c(65, 80, 85, 70)
)
ggplot(teaching_data, aes(x = Learning_Style, y = Test_Score, color = Method, group = Method)) +
geom_point(size = 5) +
geom_line(linewidth = 1.5) +
labs(title = "Interaction: Teaching Method × Learning Style",
subtitle = "Best teaching method depends on student's learning style (crossing lines!)",
x = "Learning Style",
y = "Test Score",
color = "Teaching Method") +
theme_minimal(base_size = 14) +
scale_y_continuous(limits = c(50, 90), breaks = seq(50, 90, 10)) +
theme(legend.position = "top") +
annotate("text", x = 1.5, y = 75, label = "Perfect Crossover!",
size = 5, color = "red", fontface = "bold")
```
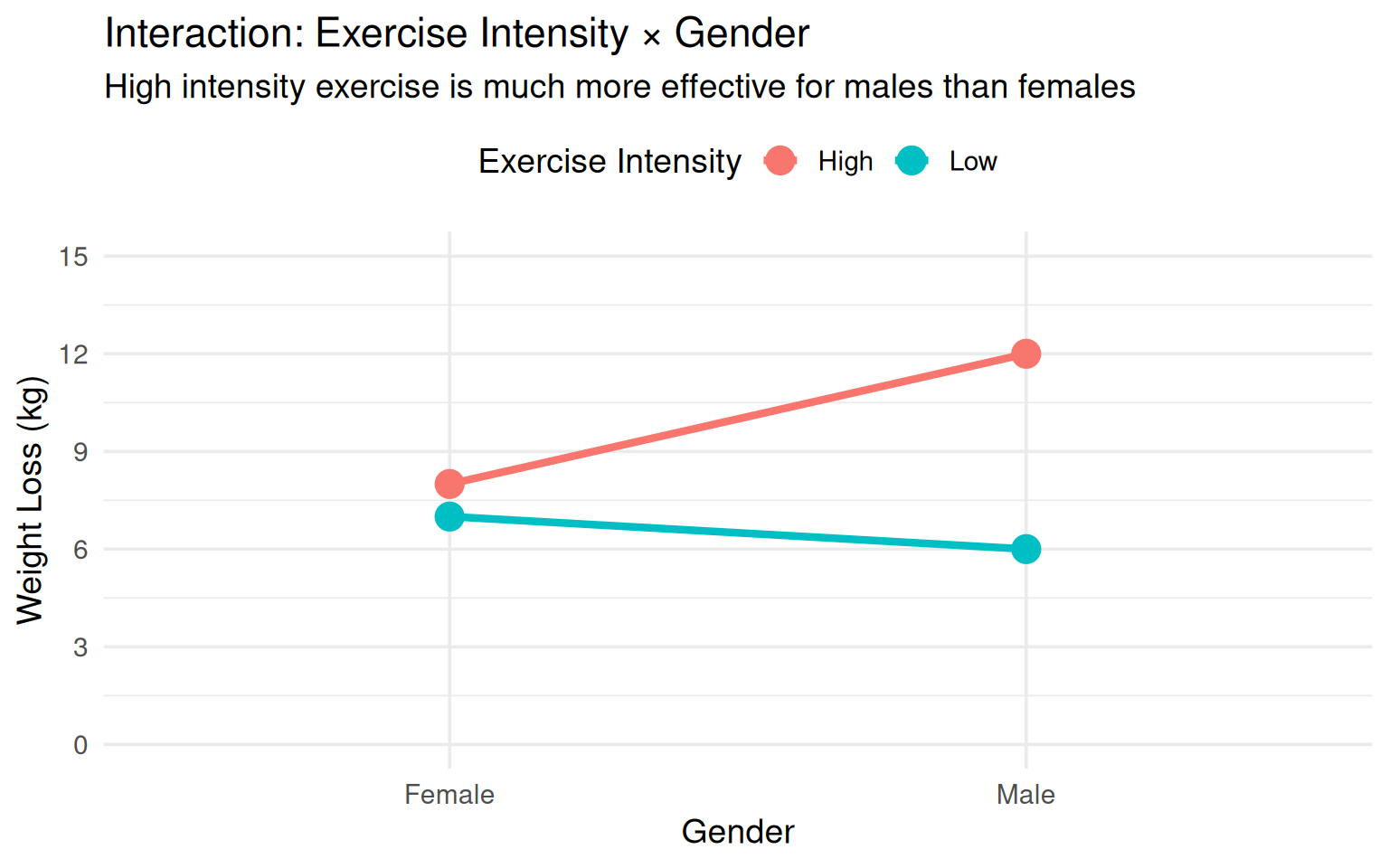
#### Example 3: Exercise & Gender
**Research Question**: Does the effect of exercise intensity on weight loss depend on biological sex?
**Factors:**
- Factor A: Exercise Intensity (Low vs. High Intensity)
- Factor B: Gender (Male vs. Female)
**Observed Pattern (Interaction Present):**
- **Males**: High intensity >> Low intensity (12 kg vs. 6 kg lost)
- **Females**: High intensity ≈ Low intensity (8 kg vs. 7 kg lost)
**Why the interaction?**
- Males typically have higher muscle mass and testosterone, enabling better response to high-intensity training
- Females may have hormonal differences affecting metabolism response to exercise intensity
- High-intensity exercise may increase cortisol more in females, potentially interfering with weight loss
- Different fat distribution patterns between sexes respond differently to exercise intensity
**Implication**: Exercise prescriptions should be **sex-specific**, not generic.
**Visualization:**
```{r}
#| echo: false
#| fig-width: 8
#| fig-height: 5
exercise_data <- data.frame(
Gender = rep(c("Male", "Female"), each = 2),
Intensity = rep(c("Low", "High"), 2),
Weight_Loss = c(6, 12, 7, 8)
)
ggplot(exercise_data, aes(x = Gender, y = Weight_Loss, color = Intensity, group = Intensity)) +
geom_point(size = 5) +
geom_line(linewidth = 1.5) +
labs(title = "Interaction: Exercise Intensity × Gender",
subtitle = "High intensity exercise is much more effective for males than females",
x = "Gender",
y = "Weight Loss (kg)",
color = "Exercise Intensity") +
theme_minimal(base_size = 14) +
scale_y_continuous(limits = c(0, 15), breaks = seq(0, 15, 3)) +
theme(legend.position = "top")
```
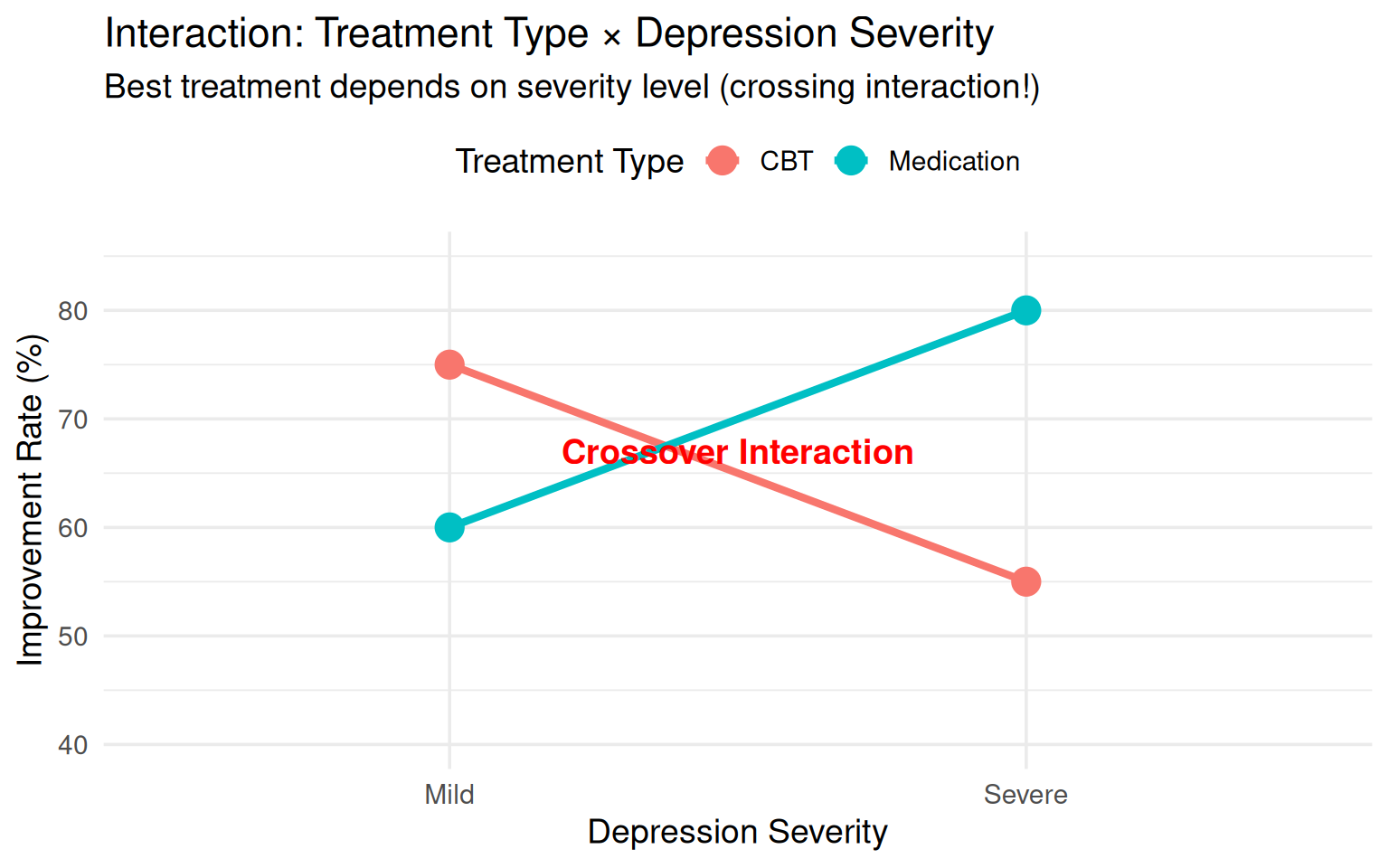
#### Example 4: Therapy & Severity
**Research Question**: Does the effectiveness of therapy type depend on depression severity?
**Factors:**
- Factor A: Therapy Type (CBT vs. Medication)
- Factor B: Depression Severity (Mild vs. Severe)
**Observed Pattern (Interaction Present):**
- **Mild Depression**: CBT >> Medication (75% vs. 60% improvement)
- **Severe Depression**: Medication >> CBT (80% vs. 55% improvement)
**Why the interaction?**
- Mild depression patients can engage effectively with cognitive strategies in CBT
- Severe depression patients may lack energy/motivation for CBT homework
- Severe cases need biological intervention (medication) to restore neurochemical balance
- CBT requires cognitive capacity that may be impaired in severe depression
**Implication**: Treatment selection should be **severity-matched**, not preference-based alone.
**Visualization:**
```{r}
#| echo: false
#| fig-width: 8
#| fig-height: 5
therapy_data <- data.frame(
Severity = rep(c("Mild", "Severe"), each = 2),
Treatment = rep(c("CBT", "Medication"), 2),
Improvement = c(75, 60, 55, 80)
)
ggplot(therapy_data, aes(x = Severity, y = Improvement, color = Treatment, group = Treatment)) +
geom_point(size = 5) +
geom_line(linewidth = 1.5) +
labs(title = "Interaction: Treatment Type × Depression Severity",
subtitle = "Best treatment depends on severity level (crossing interaction!)",
x = "Depression Severity",
y = "Improvement Rate (%)",
color = "Treatment Type") +
theme_minimal(base_size = 14) +
scale_y_continuous(limits = c(40, 85), breaks = seq(40, 85, 10)) +
theme(legend.position = "top") +
annotate("text", x = 1.5, y = 67, label = "Crossover Interaction",
size = 5, color = "red", fontface = "bold")
```
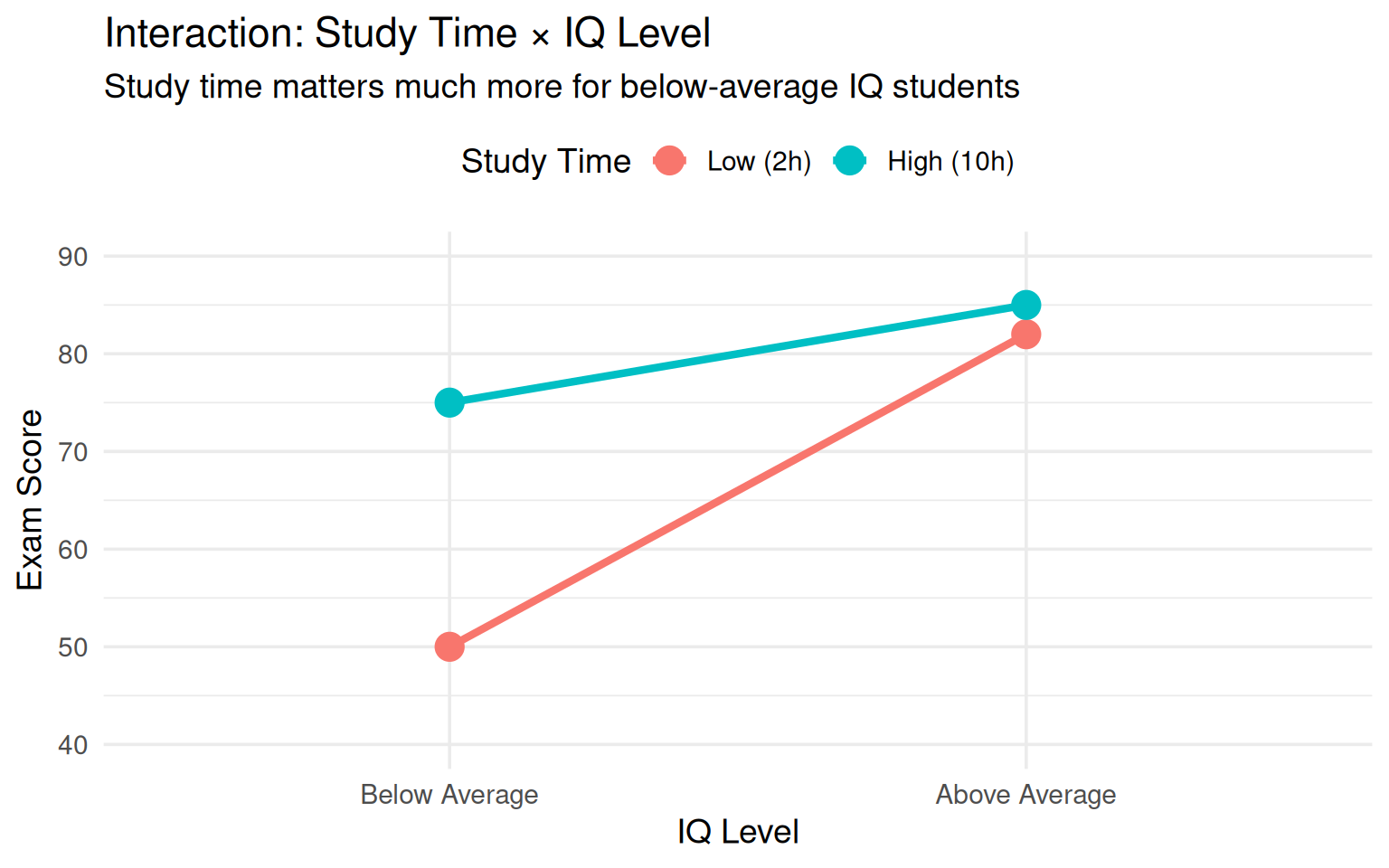
#### Example 5: Study Time & IQ
**Research Question**: Does the effect of study time on exam performance depend on intelligence level?
**Factors:**
- Factor A: Study Time (Low: 2 hrs vs. High: 10 hrs)
- Factor B: IQ Level (Below Average vs. Above Average)
**Observed Pattern (Interaction Present):**
- **Below Average IQ**: High study time >> Low study time (75 vs. 50 points)
- **Above Average IQ**: High study time ≈ Low study time (85 vs. 82 points)
**Why the interaction?**
- High IQ students can learn material efficiently with less study time
- Below average IQ students need more repetition and practice (more study time helps significantly)
- High IQ students may reach a "ceiling effect" - already performing well with minimal study
- Different cognitive abilities create different learning curves
**Implication**: Educational interventions (increasing study time) may be most beneficial for students who struggle, not top performers.
**Visualization:**
```{r}
#| echo: false
#| fig-width: 8
#| fig-height: 5
study_data <- data.frame(
IQ_Level = rep(c("Below Average", "Above Average"), each = 2),
Study_Time = rep(c("Low (2h)", "High (10h)"), 2),
Exam_Score = c(50, 75, 82, 85)
)
study_data$IQ_Level <- factor(study_data$IQ_Level, levels = c("Below Average", "Above Average"))
study_data$Study_Time <- factor(study_data$Study_Time, levels = c("Low (2h)", "High (10h)"))
ggplot(study_data, aes(x = IQ_Level, y = Exam_Score, color = Study_Time, group = Study_Time)) +
geom_point(size = 5) +
geom_line(linewidth = 1.5) +
labs(title = "Interaction: Study Time × IQ Level",
subtitle = "Study time matters much more for below-average IQ students",
x = "IQ Level",
y = "Exam Score",
color = "Study Time") +
theme_minimal(base_size = 14) +
scale_y_continuous(limits = c(40, 90), breaks = seq(40, 90, 10)) +
theme(legend.position = "top")
```
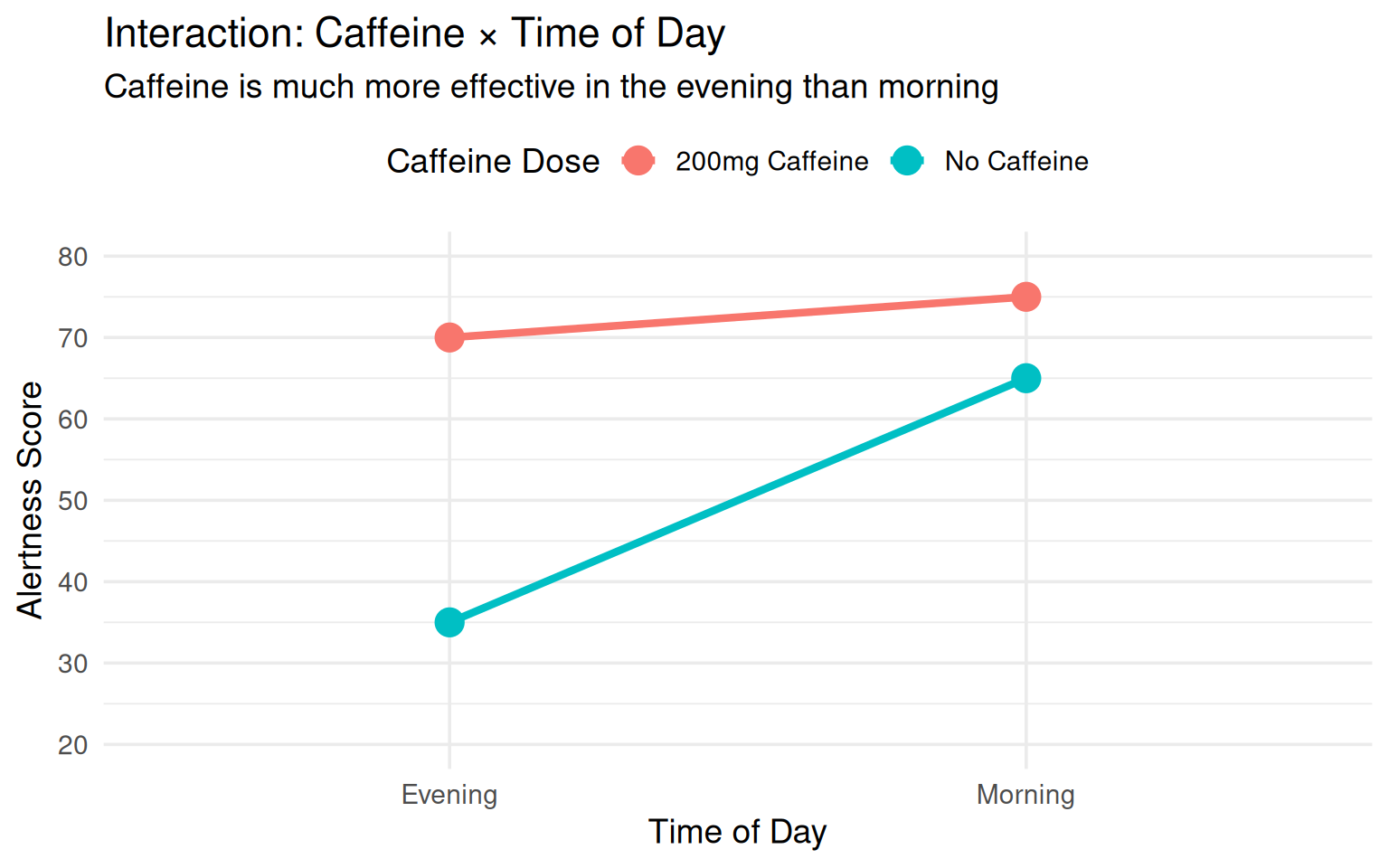
#### Example 6: Caffeine & Time of Day
**Research Question**: Does caffeine's effect on alertness depend on time of day?
**Factors:**
- Factor A: Caffeine Dose (0 mg vs. 200 mg)
- Factor B: Time of Day (Morning vs. Evening)
**Observed Pattern (Interaction Present):**
- **Morning**: Small caffeine effect (alertness: 65 vs. 75)
- **Evening**: Large caffeine effect (alertness: 35 vs. 70)
**Why the interaction?**
- Morning: Natural cortisol levels are already high (circadian rhythm), so caffeine adds less
- Evening: Cortisol levels drop naturally, so caffeine has a larger stimulating effect
- Adenosine (sleepiness molecule) accumulates throughout the day - caffeine blocks adenosine receptors
- Baseline alertness differs dramatically by time of day
**Implication**: Timing caffeine intake strategically (avoiding morning when cortisol is high) may be more effective.
**Visualization:**
```{r}
#| echo: false
#| fig-width: 8
#| fig-height: 5
caffeine_data <- data.frame(
Time = rep(c("Morning", "Evening"), each = 2),
Caffeine = rep(c("No Caffeine", "200mg Caffeine"), 2),
Alertness = c(65, 75, 35, 70)
)
ggplot(caffeine_data, aes(x = Time, y = Alertness, color = Caffeine, group = Caffeine)) +
geom_point(size = 5) +
geom_line(linewidth = 1.5) +
labs(title = "Interaction: Caffeine × Time of Day",
subtitle = "Caffeine is much more effective in the evening than morning",
x = "Time of Day",
y = "Alertness Score",
color = "Caffeine Dose") +
theme_minimal(base_size = 14) +
scale_y_continuous(limits = c(20, 80), breaks = seq(20, 80, 10)) +
theme(legend.position = "top")
```
:::
## Common Themes: Why Interactions Occur
::: callout-note
### Underlying Mechanisms for Interactions
1. **Biological Differences**: Age, sex, genetics create different physiological responses
2. **Baseline/Ceiling Effects**: Different starting points or maximum capacities across groups
3. **Mechanism Differences**: Treatments work through different pathways in different populations
4. **Resource Allocation**: Limited cognitive/physical resources are used differently across contexts
5. **Moderating Variables**: Third variables (not measured) that correlate with factors
6. **Compensatory Strategies**: Different groups adapt differently to interventions
7. **Dose-Response Variation**: Sensitivity to "dosage" varies across groups
:::
-----------
::: callout-warning
### Critical Insight
**Ignoring interactions leads to incorrect conclusions!**
If you only report main effects in these examples, you would conclude:
- "Drug A works" (missing that it works mainly for elderly)
- "Problem-based learning is better" (missing that it depends on learning style)
- "High intensity exercise is better" (missing that it mainly benefits males)
**Always test and visualize interactions before interpreting main effects!**
:::
## Model 2: Two-Way ANOVA with Interaction
$$
\mathrm{Grade} = U_1(\mathrm{Tutoring}) + U_2(\mathrm{School}) + U_3(\mathrm{TutoringxSchool})
$$
There variance components (random effects) included in a full two-way ANOVA with two Factors.
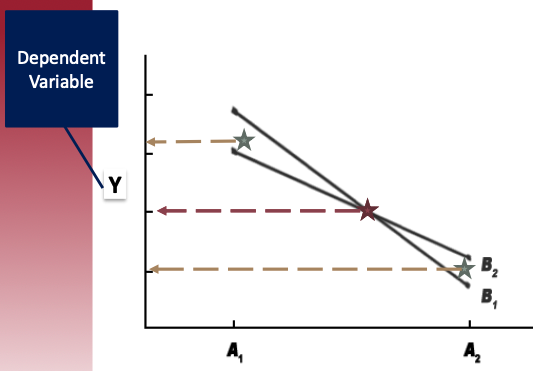
## Model 2: Visualization of Two-Way ANOVA with Interaction
::::: columns
::: column
:::
::: column
In the graph:
- There is the **LARGE** effect of Factor A and very small effect of Factor B:
- Effect of Factor A: the LARGE distance between two green stars
- Effect of Factor B: the very small distance between two red stars
In the graph, there is an intersection between two lines → This is an interaction effect between two factors!
- The level of Factor B depends upon the level of Factor A – B1 is higher than B2 for A1, but lower for A2 – B2 is lower than B1 for A1, but higher for A2
:::
:::::
# Statistical foundations of 2-way ANOVA
## F-statistics for Two-Way ANOVA
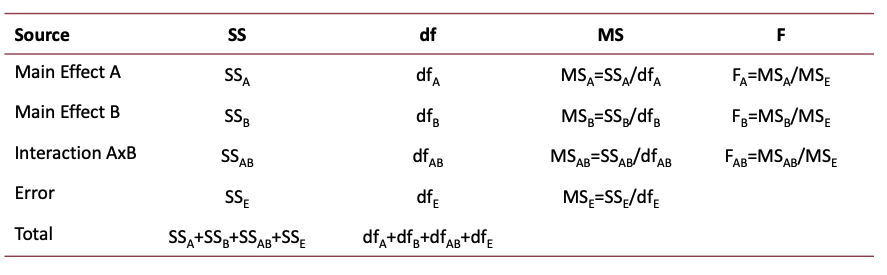
## F-statistics for Two-Way ANOVA: R code
::: panel-tabset
### R Code
```{webr-r}
summary(aov(Grades ~ Tutoring + School + Tutoring:School, data = data))
# or summary(aov(Grades ~ Tutoring*School, data = data))
```
### Interpretation
| Source | df | MS | F |
|----|----|----|----|
| Main Effect of Tutoring | 2 | $2120.1 = 4240 / 2$ | 89.065\*\*\* |
| Main Effect of School | 2 | $10.8 = 22 / 2$ | 0.636 |
| Interaction Effect of School x Tutoring | 4 | $46.5 = 186 / 4$ | 0.102 |
| Residual | 261 | $23.8 = 6213 / 261$ | --- |
:::
## F-statistics for Two-Way ANOVA: Degree of Freedom
- IVs:
1. Tutoring Programs: (1) No tutor; (2) Once a week; (3) Daily
2. Types of schools: (1) Public (2) Private-secular (3) Private-religious
- Degree of freedom (DF):
- $df_{tutoring}$ = (Number of levels of Tutoring) - 1 = 3 - 1 = 2
- $df_{school}$ = (Number of levels of School) - 1 = 3 - 1 = 2
- $df_{interaction}$ = $df_{tutoring} \times df_{school}$ = $2 \times 2$ = 4
- $df_{total}$ = 270 - 1 = 269
- $df_{residual}$ = $df_{total}-df_{tutoring}-df_{school} - df_{interaction}$ = 269 - 2 - 2 - 4= 261
::: callout-note
### Calculation of p-values
Based on DF and observed F statistics, we can locate observed F-statistic onto the F-distribution can calculate the p-values.
:::
## F-statistics for Two-Way ANOVA: SS and DF
Why residual DF is calculated by subtracting the total DFs with effects' DFs?
Because DF is linked to SS.
| Source | SS | df |
|----|----|----|
| Main Effect of Tutoring | 4240 | 2 |
| Main Effect of School | 22 | 2 |
| Interaction Effect of School x Tutoring | 186 | 4 |
| Residual | 6213 | 261 |
| Total | 4240 + 22 + 186 + 6213 | 2 + 2 + 4 + 261 |
```{r}
#| results: hold
sum((data$Grades - mean(data$Grades))^2) # manually calculate total Sum of squares
nrow(data) - 1 # nrow() calculate the number of rows / observations
```
```{r}
#| results: hold
4240 + 22 + 186 + 6213
2 + 2 + 4 + 261
```
## Difference between one-way and two-way ANOVA
::::: columns
::: column
### One-way ANOVA {.unnumbered}
Total = Between + Within
:::
::: column
### Two-way ANOVA {.unnumbered}
Total = FactorA + FactorB + A\*B + Residual
:::
:::::
::: rmdnote
*Within*-factor effects (one-way ANOVA) and *Residuals* (two-way ANOVA) have same meaning, both of which are unexplained part of DV by the model.
:::
- In Factor ANOVA Design, the overall between-group variability is divided up into variance terms for each unique source of the factors.
| Source | 2 IVs | 3 IVs | 4 IVs |
|----|----|----|----|
| Main effect | A, B | A, B, C | A, B, C, D |
| Interaction effect | AB | AB, BC, AC, ABC | AB, AC, AD, BC, BD, CD, ABC, ABD, BCD, ACD, ABCD |
::: macwindow
**Calculate the number of interaction effects** $$
\mathrm{N_{interaction}} = \sum_{j=2}^J C_J^j
$$
```{r}
##Number of interaction for 4 IVs
choose(4, 2) + choose(4, 3) + choose(4, 4)
```
:::
## F-statistics for Two-way ANOVA: F values
- F-observed values:
- Main effect of factor A: $F_A = \frac{SS_A/df_A}{SS_E/df_E} = \frac{MS_A}{MS_E}$
- $F_{tutoring} = \frac{MS_{tutoring}}{MS_{residual}} = \frac{2120.1}{23.8} = 89.065$
- Main effect of factor B: $F_B = \frac{MS_B}{MS_E}$
- $F_{School} = \frac{MS_{School}}{MS_{residual}} = \frac{10.8}{23.8} = 0.453$
- Interaction effect of AxB: $F_{AB} = \frac{MS_{AB}}{MS_E}$
- $F_{SxT} = \frac{MS_{SxT}}{MS_{residual}} = \frac{46.5}{23.8} = 1.953$
- Degree of freedom:
- $df_{tutoring}$ = (Number of levels of Tutoring) - 1
- $df_{school}$ = (Number of levels of School) - 1
- $df_{interaction}$ = $df_{tutoring} \times df_{school}$
- $df_{total}$ = N - 1
- $df_{residual}$ = $df_{total}-df_{tutoring}-df_{school} - df_{interaction}$
------------------------------------------------------------------------
## Exercise
- A new samples with N = 300
- Tutoring still has **three** levels,
- School types only have two levels: Public vs. Private.
Based on the SS provide below, calculate DF and F values for three effects.
```{webr-r}
#| context: "setup"
# Set seed for reproducibility
set.seed(1234)
# Define sample size per group
n <- 50
# Define factor levels
tutoring <- rep(c("No Tutor", "Once a Week", "Daily"), each = 2*n)
school <- rep(c("Public", "Private",
"Public", "Private",
"Public", "Private"), times = n)
# Simulate student grades with assumed effects
grades <- c(
rnorm(n, mean = 75, sd = 3), # No tutor, Public
rnorm(n, mean = 78, sd = 3), # No tutor, Private
rnorm(n, mean = 80, sd = 3), # Once a week, Public
rnorm(n, mean = 83, sd = 3), # Once a week, Private
rnorm(n, mean = 85, sd = 3), # Daily, Public
rnorm(n, mean = 88, sd = 3) # Daily, Private
)
# Create a dataframe
data2 <- data.frame(
Tutoring = factor(tutoring, levels = c("No Tutor", "Once a Week", "Daily")),
School = factor(school, levels = c("Public", "Private")),
Grades = grades
)
fit <- aov(Grades ~ Tutoring*School, data2)
fit_summary <- summary(fit)
```
```{webr-r}
#| context: "output"
fit_summary[[1]][2]
```
::: panel-tabset
### You turn
```{webr-r}
# calculate the F-values give sum of squares
df_tutoring = ______ # degree of freedom for tutoring
df_school = ______ # degree of freedom for school
df_ts = ______ # degree of freedom for interaction effects
df_res = ______ # degree of freedom for residuals
F_Tutoring = ( __ / df_tutoring ) / (__ / df_res)
F_school = (__ / df_school) / (__ / df_res)
F_ts = ( __ / df_ts) / (__ / df_res)
F_Tutoring
F_school
F_ts
```
### Result
```{webr-r}
#| read-only: true
df_res = 300 - 1 - 2 - 1 - 2
F_Tutoring = ( 5978.8 / 2) / (3571.1 / df_res)
F_school = (5.2 / 1) / (3571.1 / df_res)
F_ts = ( 3.6 / 2) / (3571.1 / df_res)
F_Tutoring
F_school
F_ts
fit_summary
```
:::
## F-statistics for Two-way ANOVA: Sum of squres
::: callout-note
In a old-fashion way, you can calculate Sum of Squares based on marginal means and sample size for each cell.
:::
::::: columns
::: column
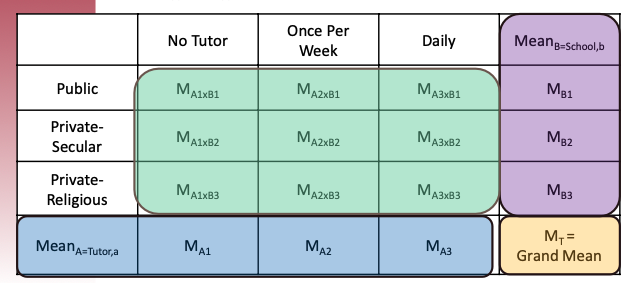
:::
::: column
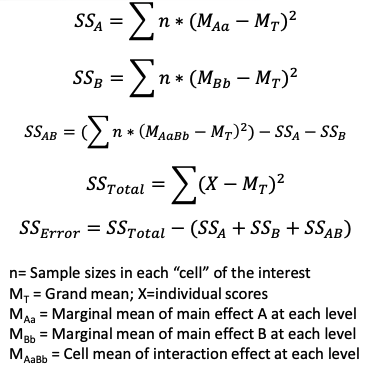
:::
:::::
## Interpretation
| Source | Df | Sum Sq | Mean Sq | F value | P |
|-----------------|-----|--------|---------|---------|----------------|
| Tutoring | 2 | 4240 | 2120.1 | 89.065 | \<2e-16 \*\*\* |
| School | 2 | 22 | 10.8 | 0.453 | 0.636 |
| Tutoring:School | 4 | 186 | 46.5 | 1.953 | 0.102 |
| Residuals | 261 | 6213 | 23.8 | | |
::: panel-tabset
### Main Effect A
- Main Effect A: Ignoring type of school, are there differences in grades across type of tutoring?
- Under alpha=.05 level, because F-observed (F_observed=89.065) exceeds the critical value (p \< .001), we reject the null that all means are equal across tutoring type (ignoring the effect of school type).
- There is a significant main effect of tutoring type on grade.
### Main Effect B
- Main Effect B: Ignoring tutoring type, are there differences in grades across type of school?
- Under alpha=.05 level, because F-observed (F_observed=95.40) exceeds the critical value (p = .453), we retain (or fail to reject) the null hypothesis that all means are equal across school type (ignoring the effect of tutoring type).
- There is no evidence suggesting a significant main effect of school type on grade.
### Interaction Effect AB
- Interaction Effect: Does the effect of tutoring type on grades depend on the type of school?
- Under alpha=.05 level, because F-observed (F_observed=2.21) does not exceed the critical value (p = 0.102), we fail to reject the null that the effect of Factor A depends on Factor B.
- There is not a significant interaction between tutoring type and school type on grades.
:::
## Assumptions for conducting 2-way ANOVA
- In order to compare our sample to the null distribution, we need to make sure we are meeting some assumptions for each CELL:
1. Variance of DV in each cell is about equal. → Homogeneity of variance\
2. DV is normally distributed within each cell. → Normality
3. Observations are independent. → Independence
- **Robustness** of assumption violations:
1. Violations of independence assumption: bad news! → Not robust to this!
2. Having a large N and equal cell sizes protects you against violations of the normality assumption → Rough suggestion: have at least 15 participants per cell → If you don’t have large N or equal groups, check cell normality 2 ways: (1) skew/kurtosis values, (2) histograms
3. Use Levene’s test to check homogeneity of cell variance assumption → If can’t assume equal variances, use Welch or Brown-Forsyth. → However, F is somewhat robust to violations of HOV as long as within-cell standard deviations are approximately equal.
## Two-way ANOVA: Calculation based on Grand & Marginal & Cell Means
::: panel-tabset
### Background
This research study is an adaptation of Gueguen (2012) described in Andy Field’s text. Specifically, the researchers hypothesized that **people with tattoos and piercings were more likely to engage in riskier behavior than those without tattoos and piercings**. In addition, the researcher wondered whether this difference varied, depending on whether a person was male or female.
Question: How many IVs? How many levels for each.
Answer: [2 IVs: (1) Whether or not having Tattos and Piercings (2) Male of Female. DV: Frequency of risk behaviors]{.mohu}
### Data screening
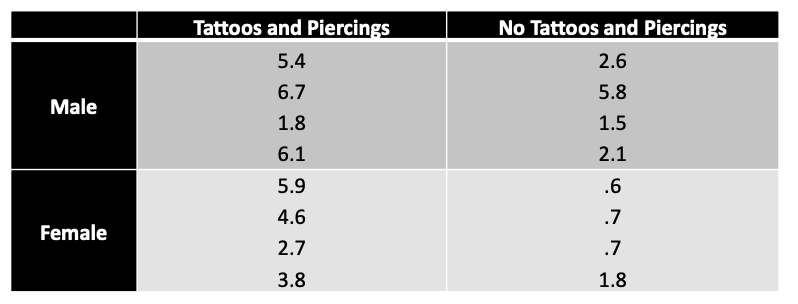
:::
## Step 1: Data importion
Either you can import a CSV file, or manually import the data points (for small samples).
Imagine you have a data with N = 16.
```{r}
tatto_piercing = rep(c(TRUE, FALSE), each = 8)
gender = rep(c("Male", "Female", "Male", "Female"), each = 4)
outcome = c(5.4, 6.7, 1.8, 6.1, 5.9, 4.6, 2.7, 3.8,
2.6, 5.8, 1.5, 2.1, .6, .7, .7, 1.8)
dat <- data.frame(
tatto_piercing = tatto_piercing,
gender = gender,
outcome = outcome
)
dat
```
## Step 2: Sum of Squares of main effects
$$
SS_A = \sum n_a (M_{Aa} - M_T)^2
$$
- $M_{Aa}$ marginal mean of main effect A at each level
- $n_a$: sample size for factor A at each level
- $M_T$: grand mean of outcome
----------------------------
### Obtain sum of square of tatto piercing
```{r}
#| include: false
summary(aov(data = dat, formula = outcome ~ gender * tatto_piercing))
```
#### Manual way
```{r}
M_A_table <- dat |>
group_by(tatto_piercing) |>
summarise(
N = n(),
Mean = mean(outcome)
)
M_T = mean(dat$outcome)
M_A_table
```
```{r}
M_A_table$N[1] * (M_A_table$Mean[1] - M_T)^2 +
M_A_table$N[2] * (M_A_table$Mean[2] - M_T)^2
```
or
```{r}
sum(M_A_table$N * (M_A_table$Mean - M_T)^2)
```
------------------------------------------------------------------------
### Your turn: Obtain sum of squares of gender
```{webr-r}
#| context: setup
tatto_piercing = rep(c(TRUE, FALSE), each = 8)
gender = rep(c("Male", "Female", "Male", "Female"), each = 4)
outcome = c(5.4, 6.7, 1.8, 6.1, 5.9, 4.6, 2.7, 3.8,
2.6, 5.8, 1.5, 2.1, .6, .7, .7, 1.8)
dat <- data.frame(
tatto_piercing = tatto_piercing,
gender = gender,
outcome = outcome
)
dat
```
::: panel-tabset
### Exercise
`dat` object has already been loaded into R. Please, calculate the gender's sum of squares:
```{webr-r}
M_B_table <- dat |>
group_by(____) |>
summarise(
N = n(),
Mean = mean(___)
)
M_T = mean(____) ## grand mean
M_B_table
## Formula for Sum of squares of Gender
___[1] * (____[1] - ___)^2 +
___[2] * (____[2] - ____)^2
```
### Answer
```{webr-r}
M_B_table <- dat |>
group_by(gender) |>
summarise(
N = n(),
Mean = mean(outcome)
)
M_T = mean(dat$outcome) ## grand mean
M_B_table
M_B_table$N[1] * (M_B_table$Mean[1] - M_T)^2 +
M_B_table$N[2] * (M_B_table$Mean[2] - M_T)^2
```
:::
## Step 3: Sum of Squares of interaction effect
$$
SS_{AB} = (\sum n_{ab} (M_{AaBb} - M_T)^2) - SS_A - SS_B
$$

```{r}
cell_means <- dat |>
group_by(tatto_piercing, gender) |>
summarise(
N = n(),
Mean = mean(outcome)
)
cell_means
```
------------------------------------------------------------------------
### Your turn
The data frame --- `cell_means` is already available to you.
```{webr-r}
#| context: setup
cell_means <- dat |>
group_by(tatto_piercing, gender) |>
summarise(
N = n(),
Mean = mean(outcome)
)
```
::: panel-tabset
### Exercise
Note: Sum of squares of interaction effects is the leftover of total sum of squares after removing SS of gender and SS of tutoring program.
$SS_{total} = \Sigma (N_{ab} * (M_{ab} - M_T))$
where $N_{ab}$ is the cell sample size for a-level of factor A and b-level of factor B.
$M_{ab}$ is the cell means of outcome; $M_T$ is the grand mean of outcome.
```{webr-r}
SS_gender <- 7.84
SS_TP <- 28.09
M_T <- 3.3
SS_total <- sum(____ * (____ - ___)^2)
SS_GxTP <- SS_total - ____ - ____
print(SS_GxTP)
```
### Answer
```{webr-r}
SS_gender <- 7.84
SS_TP <- 28.09
M_T <- 3.3
SS_total <- sum(____ * (____ - ___)^2)
SS_GxTP <- SS_total - ____ - ____
print(SS_GxTP)
sum(cell_means$N * (cell_means$Mean - M_T)^2) - SS_gender - SS_TP
```
:::
## Step 4: Calculate Degree of freedom and F-statistics
::: panel-tabset
### Your turn
```{webr-r}
#| context: setup
SS_gender <- 7.84
SS_TP <- 28.09
M_T <- 3.3
SS_GxTP <- sum(cell_means$N * (cell_means$Mean - M_T)^2) - SS_gender - SS_TP
SS_total <- sum((dat$outcome - mean(dat$outcome))^2)
SS_residual = SS_total - SS_gender - SS_TP - SS_GxTP
```
```{webr-r}
## Calculate total sum of square and residual SS
SS_total <- sum((dat$outcome - mean(dat$outcome))^2)
SS_residual = SS_total - SS_gender - SS_TP - SS_GxTP
df_gender = ___ # degree of freedom of factor gender
df_TP = ___ # degree of freedom of factor tutoring
df_GxTP = _____ # degree of freedom of interaction term gender x tutoring
df_residual = __ - __ - __ - __ - ___ # degree of freedom of residuals
F_gender = (___ / df_gender) / (SS_residual / df_residual)
F_TP = (___ / df_TP) / (SS_residual / df_residual)
F_GxTP = (___ / df_GxTP) / (SS_residual / df_residual)
F_gender; F_TP; F_GxTP # print out three F-statistics
```
### Answer
```{webr-r}
df_gender = 1
df_TP = 1
df_GxTP = 1*1
df_residual = 16 - 1 - 1 - 1 - 1*1
F_gender = (SS_gender / df_gender) / (SS_residual / df_residual)
F_TP = (SS_TP / df_TP) / (SS_residual / df_residual)
F_GxTP = (SS_GxTP / df_GxTP) / (SS_residual / df_residual)
F_gender; F_TP; F_GxTP # print out three F-statistics
# Df Sum Sq Mean Sq F value Pr(>F)
# gender 1 7.84 7.840 2.942 0.112
# tatto_piercing 1 28.09 28.090 10.540 0.007 **
# gender:tatto_piercing 1 1.69 1.690 0.634 0.441
# Residuals 12 31.98 2.665
```
:::
## Interpretation
```
# Df Sum Sq Mean Sq F value Pr(>F)
# gender 1 7.84 7.840 2.942 0.112
# tatto_piercing 1 28.09 28.090 10.540 0.007 **
# gender:tatto_piercing 1 1.69 1.690 0.634 0.441
# Residuals 12 31.98 2.665
```
- Main Effect of Tattoo-Piercing: Reject the null → Ignoring the gender, there is a significant main effect of tattoo on risky behavior.
- Main Effect of Gender: Retain the null → Ignoring the tattoo, there is NO significant main effect of gender on risky behavior.
- Interaction: Retain the null → Under alpha=.05 level, because F-observed (F=0.63) does not exceed the critical value (F=4.75), we fail to reject the null that the effect of Factor A depends on Factor B. → “There is NO significant interaction between gender and tattoo on risky behavior.”
## Final discussion
In this example,
- The interaction effect shows several issues:
- Violation of independency assumption
- Violation of normality assumption in the condition of "Male" and "Tattoo=Yes"
- We can guess/think about one possibility that it might be cause by several reasons. (e.g., too small sample sizes, not randomized assignments of the samples, not a significant interaction effect, etc.)
- From the two-way ANOVA results, we found that the interaction effect is not significant.
- Thus, in this case, it is more reasonable to conduct
1. one-way ANOVA for "Group" variable, and
2. one-way ANOVA for "Gender" variable, separately.
- For each of one-way ANOVAs, we should check the assumptions, conduct one-way ANOVA, and post-hoc test separately as well.
## Type I Sum of Squares
- Type I / Type II / Type III sum of squares?
- Effect sums of squares ($SS_A$, $SS_B$, $SS_{AB}$) are a decomposition of the total sum of squared deviations from the overall mean (SST).
- How the $SS_T$ is decomposed depends on characteristics of the data as well as the hypotheses of interest to the researcher.
- Type I sums of squares (SS) are based on a sequential decomposition.
- For example, if your ANOVA model statement is “MODEL Y = A B A\*B”, then, the sum of squares are considered in effect order A, B, A\*B, with each effect adjusted for all preceding effects in the model.
- Thus, any variance that is shared between the various effects will be sub-summed by the variable entered earlier.
Pros:
1. Nice property: balanced or not, SS for all the effects add up to the total SS, a complete decomposition of the predicted sums of squares for the whole model. This is not generally true for any other type of sums of squares.
2. Preferable when some factors (such as nesting) should be taken out before other factors. For example, with unequal number of male and female, factor "gender" should precede "subject" in an unbalanced design.
Cons: 1. Order matters! 2. Not appropriate for factorial designs, but might be ok for Blocking designs.
## Type II Sum of Squares
- With Type II SS, each main effect is considered as though it were added after the other main effects but before the interaction.
- Any interaction effects are calculated based on a model already containing the main effects.
- Any variance that is shared between A and B is not considered part of A or B.
- Thus, interaction variance that is shared with A or with B will be counted as part of the main effect, and not as part of the interaction effect.
Pros:
1. appropriate for model building, and natural choice for regression
2. most powerful when there is no interaction
3. invariant to the order in which effects are entered into the model
Cons:
1. For factorial designs with unequal cell samples, Type II sums of squares test hypotheses that are complex functions of the cell so that ordinarily are not meaningful.
2. Not appropriate for factorial designs.
## Type III Sum of Squares
- Type III SS considers all effects as though they are added last.
- Any shared variance ends up not being counted in any of the effects.
- In ANOVA, when the data are balanced (equal cell sizes) and the factors are orthogonal and all three types of sums of squares are identical.
- Orthogonal, or independent, indicates that there is no variance shared across the various effects, and the separate sums of squares can be added to obtain the model sums of squares.
Pros:
Not sample size dependent: effect estimates are not a function of the frequency of observations in any group (i.e., for unbalanced data, where we have unequal numbers of observations in each group).
Cons:
Not appropriate for designs with missing cells: for ANOVA designs with missing cells, Type III sums of squares generally do not test hypotheses about least squares means, but instead test hypotheses that are complex functions of the patterns of missing cells in higher-order containing interactions and that are ordinarily not meaningful.
::: rmdnote
In general, for the factorial design, we usually report Type III SS, unless you have missing cells in your model.
:::
## Exercise: Two-Way ANOVA with Significant Interaction
::: panel-tabset
### Background
A researcher is investigating the effect of **learning environment** (Online vs. In-Person) and **feedback type** (Immediate vs. Delayed) on student test scores. The researcher hypothesizes that:
1. Students in in-person classes will perform better than online students
2. Immediate feedback will lead to better performance than delayed feedback
3. **The benefit of immediate feedback will be stronger in online environments** (interaction effect)
The study randomly assigned 20 students to one of four conditions:
- Online + Immediate Feedback (n=5)
- Online + Delayed Feedback (n=5)
- In-Person + Immediate Feedback (n=5)
- In-Person + Delayed Feedback (n=5)
**Your Task**: Calculate the sum of squares for both main effects and the interaction effect manually, then compute F-statistics.
### View Data Summary
```{webr-r}
#| context: setup
set.seed(456)
# Create data with significant interaction
learning_env <- rep(c("Online", "In-Person"), each = 10)
feedback_type <- rep(c("Immediate", "Delayed"), times = 10)
# Test scores - designed to show interaction
# Online + Immediate: high scores (mean ~85)
# Online + Delayed: low scores (mean ~70)
# In-Person + Immediate: moderate scores (mean ~78)
# In-Person + Delayed: moderate-high scores (mean ~82)
test_scores <- c(
# Online + Immediate
87, 83, 88, 86, 81,
# Online + Delayed
68, 72, 71, 69, 70,
# In-Person + Immediate
79, 77, 80, 76, 78,
# In-Person + Delayed
84, 81, 83, 80, 82
)
exercise_data <- data.frame(
Learning_Env = factor(learning_env, levels = c("Online", "In-Person")),
Feedback = factor(feedback_type, levels = c("Immediate", "Delayed")),
Score = test_scores
)
# Display the data
exercise_data
```
```{webr-r}
# Cell means
cell_summary <- exercise_data |>
group_by(Learning_Env, Feedback) |>
summarise(
N = n(),
Mean = mean(Score),
SD = sd(Score)
)
print(cell_summary)
# Marginal means for Learning Environment
marginal_env <- exercise_data |>
group_by(Learning_Env) |>
summarise(
N = n(),
Mean = mean(Score)
)
print(marginal_env)
# Marginal means for Feedback Type
marginal_feedback <- exercise_data |>
group_by(Feedback) |>
summarise(
N = n(),
Mean = mean(Score)
)
print(marginal_feedback)
# Grand mean
grand_mean <- mean(exercise_data$Score)
print(paste("Grand Mean:", round(grand_mean, 2)))
```
### Step 1: Calculate SS for Learning Environment
**Formula**: $SS_A = \sum n_a (M_{Aa} - M_T)^2$
where:
- $M_{Aa}$ = marginal mean of Learning Environment at each level
- $n_a$ = sample size for each level of Learning Environment
- $M_T$ = grand mean
```{webr-r}
# Calculate marginal means for Learning Environment
M_Env_table <- exercise_data |>
group_by(Learning_Env) |>
summarise(
N = n(),
Mean = mean(Score)
)
M_T <- mean(exercise_data$Score) # Grand mean
# Calculate SS for Learning Environment
SS_Env <- ___[1] * (___[1] - ___)^2 +
___[2] * (___[2] - ___)^2
print(paste("SS for Learning Environment:", round(SS_Env, 2)))
```
### Step 2: Calculate SS for Feedback Type
**Formula**: $SS_B = \sum n_b (M_{Bb} - M_T)^2$
```{webr-r}
# Calculate marginal means for Feedback Type
M_Feedback_table <- exercise_data |>
group_by(____) |>
summarise(
N = n(),
Mean = mean(____)
)
M_T <- mean(____) # Grand mean
# Calculate SS for Feedback Type
SS_Feedback <- ____$N[1] * (____$Mean[1] - ____)^2 +
____$N[2] * (____$Mean[2] - ____)^2
print(paste("SS for Feedback Type:", round(SS_Feedback, 2)))
```
### Step 3: Calculate SS for Interaction
**Formula**: $SS_{AB} = (\sum n_{ab} (M_{AaBb} - M_T)^2) - SS_A - SS_B$
```{webr-r}
# Calculate cell means
cell_means_table <- exercise_data |>
group_by(____, ____) |>
summarise(
N = n(),
Mean = mean(____)
)
print(cell_means_table)
# Calculate total SS from cells
SS_total_cells <- sum(____$N * (____$Mean - ____)^2)
# Calculate interaction SS
SS_Interaction <- ____ - ____ - ____
print(paste("SS for Interaction:", round(SS_Interaction, 2)))
```
### Step 4: Calculate F-statistics
```{webr-r}
# Calculate residual SS
SS_total <- sum((exercise_data$Score - mean(exercise_data$Score))^2)
SS_residual <- ____ - ____ - ____ - ____
# Calculate degrees of freedom
df_Env <- ____ # levels - 1
df_Feedback <- ____ # levels - 1
df_Interaction <- ____ * ____ # df_Env * df_Feedback
df_residual <- 20 - ____ - ____ - ____ - ____
# Calculate F-statistics
F_Env <- (SS_Env / df_Env) / (____ / ____)
F_Feedback <- (____ / ____) / (SS_residual / df_residual)
F_Interaction <- (____ / ____) / (____ / ____)
print(paste("F for Learning Environment:", round(F_Env, 3)))
print(paste("F for Feedback Type:", round(F_Feedback, 3)))
print(paste("F for Interaction:", round(F_Interaction, 3)))
```
### Answer - Step 1
```{webr-r}
# Calculate marginal means for Learning Environment
M_Env_table <- exercise_data |>
group_by(Learning_Env) |>
summarise(
N = n(),
Mean = mean(Score)
)
M_T <- mean(exercise_data$Score) # Grand mean
# Calculate SS for Learning Environment
SS_Env <- M_Env_table$N[1] * (M_Env_table$Mean[1] - M_T)^2 +
M_Env_table$N[2] * (M_Env_table$Mean[2] - M_T)^2
print(paste("SS for Learning Environment:", round(SS_Env, 2)))
```
### Answer - Step 2
```{webr-r}
# Calculate marginal means for Feedback Type
M_Feedback_table <- exercise_data |>
group_by(Feedback) |>
summarise(
N = n(),
Mean = mean(Score)
)
M_T <- mean(exercise_data$Score) # Grand mean
# Calculate SS for Feedback Type
SS_Feedback <- M_Feedback_table$N[1] * (M_Feedback_table$Mean[1] - M_T)^2 +
M_Feedback_table$N[2] * (M_Feedback_table$Mean[2] - M_T)^2
print(paste("SS for Feedback Type:", round(SS_Feedback, 2)))
```
### Answer - Step 3
```{webr-r}
# Calculate cell means
cell_means_table <- exercise_data |>
group_by(Learning_Env, Feedback) |>
summarise(
N = n(),
Mean = mean(Score)
)
print(cell_means_table)
# Calculate total SS from cells
SS_total_cells <- sum(cell_means_table$N * (cell_means_table$Mean - M_T)^2)
# Calculate interaction SS
SS_Interaction <- SS_total_cells - SS_Env - SS_Feedback
print(paste("SS for Interaction:", round(SS_Interaction, 2)))
```
### Answer - Step 4
```{webr-r}
# Calculate residual SS
SS_total <- sum((exercise_data$Score - mean(exercise_data$Score))^2)
SS_residual <- SS_total - SS_Env - SS_Feedback - SS_Interaction
# Calculate degrees of freedom
df_Env <- 1 # 2 levels - 1
df_Feedback <- 1 # 2 levels - 1
df_Interaction <- 1 * 1 # df_Env * df_Feedback
df_residual <- 20 - 1 - 1 - 1 - 1
# Calculate F-statistics
F_Env <- (SS_Env / df_Env) / (SS_residual / df_residual)
F_Feedback <- (SS_Feedback / df_Feedback) / (SS_residual / df_residual)
F_Interaction <- (SS_Interaction / df_Interaction) / (SS_residual / df_residual)
print(paste("F for Learning Environment:", round(F_Env, 3)))
print(paste("F for Feedback Type:", round(F_Feedback, 3)))
print(paste("F for Interaction:", round(F_Interaction, 3)))
# Calculate p-values
p_Env <- pf(F_Env, df_Env, df_residual, lower.tail = FALSE)
p_Feedback <- pf(F_Feedback, df_Feedback, df_residual, lower.tail = FALSE)
p_Interaction <- pf(F_Interaction, df_Interaction, df_residual, lower.tail = FALSE)
print(paste("p-value for Learning Environment:", round(p_Env, 4)))
print(paste("p-value for Feedback Type:", round(p_Feedback, 4)))
print(paste("p-value for Interaction:", round(p_Interaction, 4)))
```
### Verify with R's aov()
```{webr-r}
# Verify your calculations with R's built-in ANOVA
fit <- aov(Score ~ Learning_Env * Feedback, data = exercise_data)
summary(fit)
```
### Interpretation
```{webr-r}
# Visualize the interaction
library(ggplot2)
interaction_plot <- exercise_data |>
group_by(Learning_Env, Feedback) |>
summarise(Mean_Score = mean(Score)) |>
ggplot(aes(x = Learning_Env, y = Mean_Score, color = Feedback, group = Feedback)) +
geom_point(size = 4) +
geom_line(linewidth = 1.2) +
labs(title = "Interaction Plot: Learning Environment × Feedback Type",
x = "Learning Environment",
y = "Mean Test Score",
color = "Feedback Type") +
theme_minimal() +
theme(text = element_text(size = 12))
print(interaction_plot)
```
**Key Findings:**
1. **Main Effect of Learning Environment**: The effect depends on whether it's significant (check your F-statistic and p-value)
2. **Main Effect of Feedback Type**: The effect depends on whether it's significant (check your F-statistic and p-value)
3. **Interaction Effect**: **This should be significant!** The interaction plot shows that:
- In **Online** environments, Immediate feedback leads to MUCH higher scores than Delayed feedback
- In **In-Person** environments, the difference between Immediate and Delayed feedback is smaller (and reversed!)
- This crossing pattern indicates a strong interaction: the effect of feedback type depends on the learning environment
:::
## Lecture Summary: Key Takeaways
::: callout-tip
### 1. Conceptual Understanding
**Two-way ANOVA allows us to:**
- Examine the effects of **two independent variables** simultaneously
- Test for **three distinct effects**: Main effect A, Main effect B, and Interaction A×B
- Investigate whether the effect of one factor **depends on** the level of another factor (interaction)
- Achieve greater statistical power and efficiency compared to multiple one-way ANOVAs
**Main Effects vs. Interaction:**
- **Main Effect**: The average effect of one factor, ignoring (collapsing across) the other factor
- **Interaction Effect**: When the effect of one factor changes depending on the level of the other factor
- Look for **non-parallel lines** in interaction plots
- **Crossing lines** indicate strong interactions
- When interaction is significant, main effects may be misleading!
:::
-------------------
::: callout-important
### 2. Statistical Calculations
**Partitioning Variance in Two-Way ANOVA:**
$$
SS_{Total} = SS_A + SS_B + SS_{AB} + SS_{Residual}
$$
**Key Formulas:**
- Main Effect A: $SS_A = \sum n_a (M_{Aa} - M_T)^2$
- Main Effect B: $SS_B = \sum n_b (M_{Bb} - M_T)^2$
- Interaction: $SS_{AB} = (\sum n_{ab} (M_{AaBb} - M_T)^2) - SS_A - SS_B$
**F-statistics:**
$$
F = \frac{MS_{effect}}{MS_{residual}} = \frac{SS_{effect}/df_{effect}}{SS_{residual}/df_{residual}}
$$
**Degrees of Freedom:**
- $df_A = k_A - 1$ (number of levels of Factor A minus 1)
- $df_B = k_B - 1$ (number of levels of Factor B minus 1)
- $df_{AB} = df_A \times df_B$ (interaction df)
- $df_{residual} = N - 1 - df_A - df_B - df_{AB}$
:::
-------------------
::: callout-note
### 3. Practical Considerations
**Assumptions for Two-Way ANOVA:**
1. **Independence**: Observations must be independent (most critical!)
2. **Normality**: DV should be normally distributed within each cell
3. **Homogeneity of Variance**: Equal variances across all cells (Levene's test)
**Robustness:**
- F-test is fairly robust to normality violations with large N and equal cell sizes
- Recommend at least **15 participants per cell**
- Use Welch or Brown-Forsythe tests if variances are unequal
- **Never** compromise on independence assumption
**Type I, II, III Sum of Squares:**
- **Type I**: Sequential (order matters) - appropriate for nested/blocking designs
- **Type II**: Each main effect adjusted for other main effects - good for model building
- **Type III**: Each effect adjusted for all others - **recommended for factorial designs** with balanced data
- With **balanced designs** (equal cell sizes), all three types give identical results!
:::
-------------------
::: callout-warning
### 4. Interpretation Guidelines
**When Interaction is Significant:**
- Interpret interaction **first** before discussing main effects
- Main effects may be misleading or uninterpretable when interaction is present
- Focus on **simple effects**: the effect of one factor at each level of the other
- Use interaction plots to visualize and explain the pattern
**When Interaction is NOT Significant:**
- Proceed to interpret main effects
- If main effect is significant with >2 levels, conduct **post-hoc tests** (e.g., Tukey HSD)
- Report effect sizes (partial η²) alongside p-values
**Reporting Results:**
Include in your report:
1. Descriptive statistics (means, SDs) for all cells
2. ANOVA table with F-values, df, and p-values
3. Effect sizes
4. Interaction plot (even if not significant)
5. Post-hoc tests if needed
6. Assumption checks
:::
-------------------
::: callout-tip
### 5. Common Pitfalls to Avoid
1. **Don't ignore significant interactions!** Main effects alone don't tell the whole story
2. **Don't forget assumption checks** - especially for small samples
3. **Don't confuse interaction with correlation** - they are different concepts
4. **Don't over-interpret non-significant results** - absence of evidence ≠ evidence of absence
5. **Don't use multiple one-way ANOVAs instead of two-way** - you'll miss interactions and inflate Type I error
6. **Don't forget to report effect sizes** - statistical significance ≠ practical significance
:::
-------------------
::: callout-important
### 6. Next Steps in Your Learning
**Extending Two-Way ANOVA:**
- **Three-way ANOVA**: Adding a third factor (exponentially more complex!)
- **Mixed ANOVA**: Combining between-subjects and within-subjects factors
- **ANCOVA**: Adding continuous covariates to control for confounding variables
- **MANOVA**: Multiple dependent variables simultaneously
- **Repeated Measures ANOVA**: Same subjects measured multiple times
**When to Use Two-Way ANOVA:**
✓ Two categorical independent variables (factors)
✓ One continuous dependent variable
✓ Independent observations (between-subjects design)
✓ Interest in both main effects and interaction
✓ Adequate sample size (≥15 per cell recommended)
**Alternatives to Consider:**
- **Regression with interactions**: More flexible, can handle continuous IVs
- **Mixed-effects models**: Better for unbalanced designs or nested data
- **Non-parametric tests**: When assumptions are severely violated (e.g., Aligned Rank Transform ANOVA)
:::
## Fin
**Thank you for your attention!**