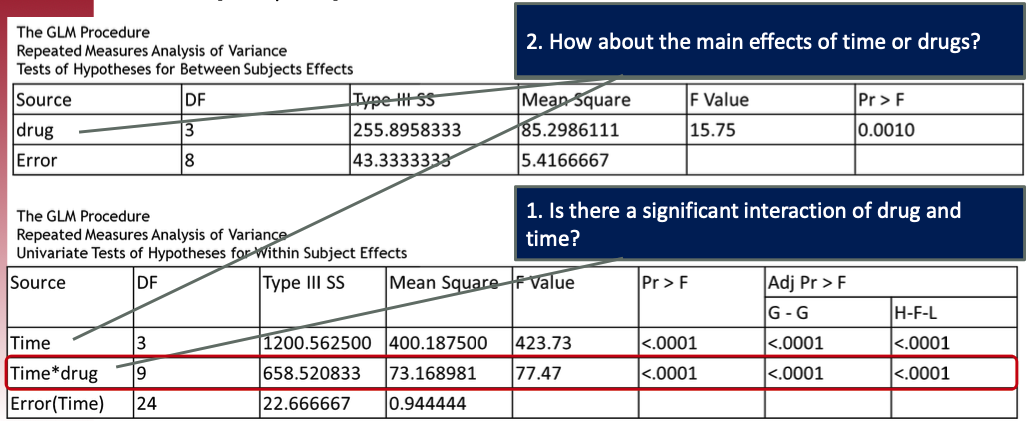
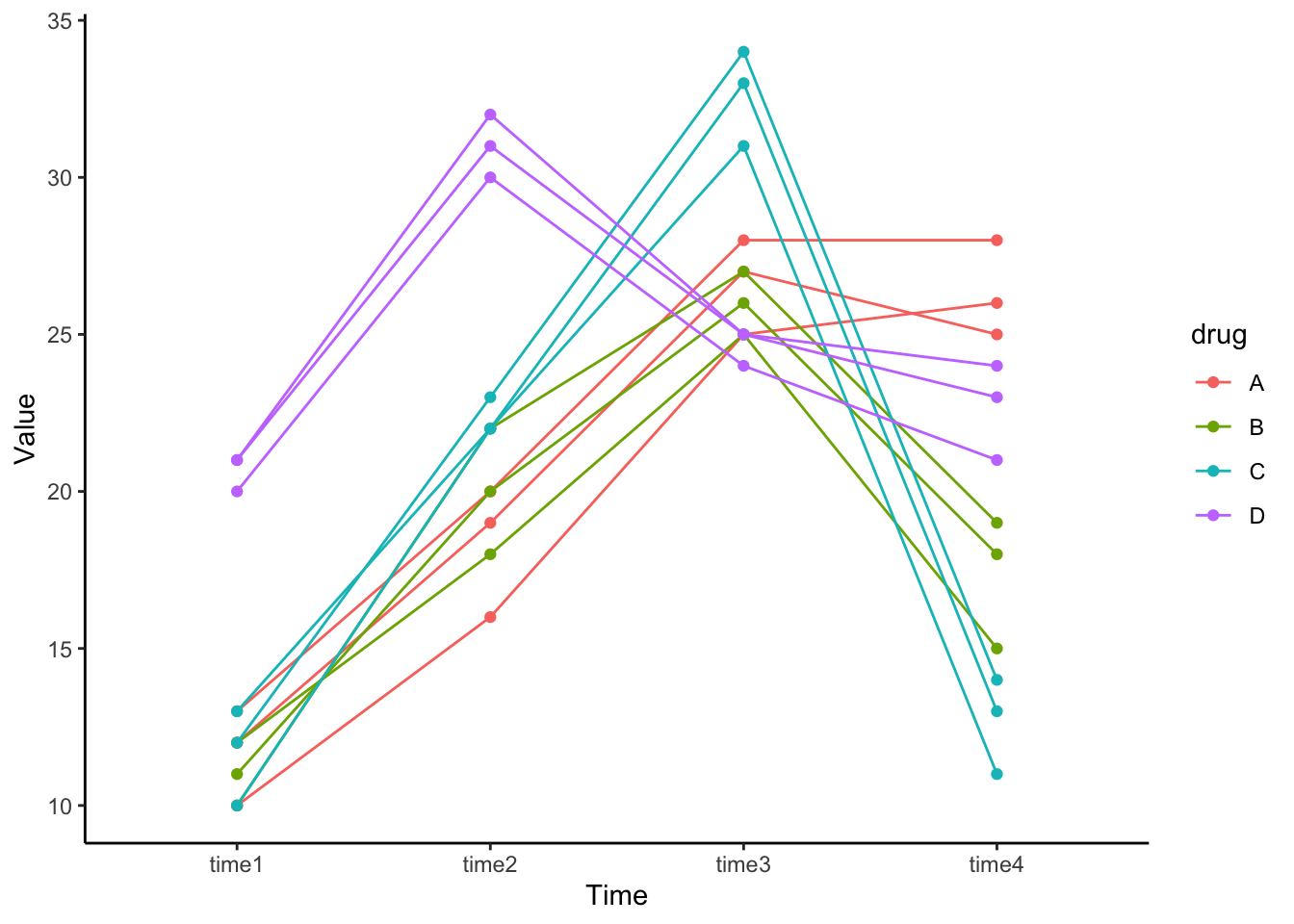
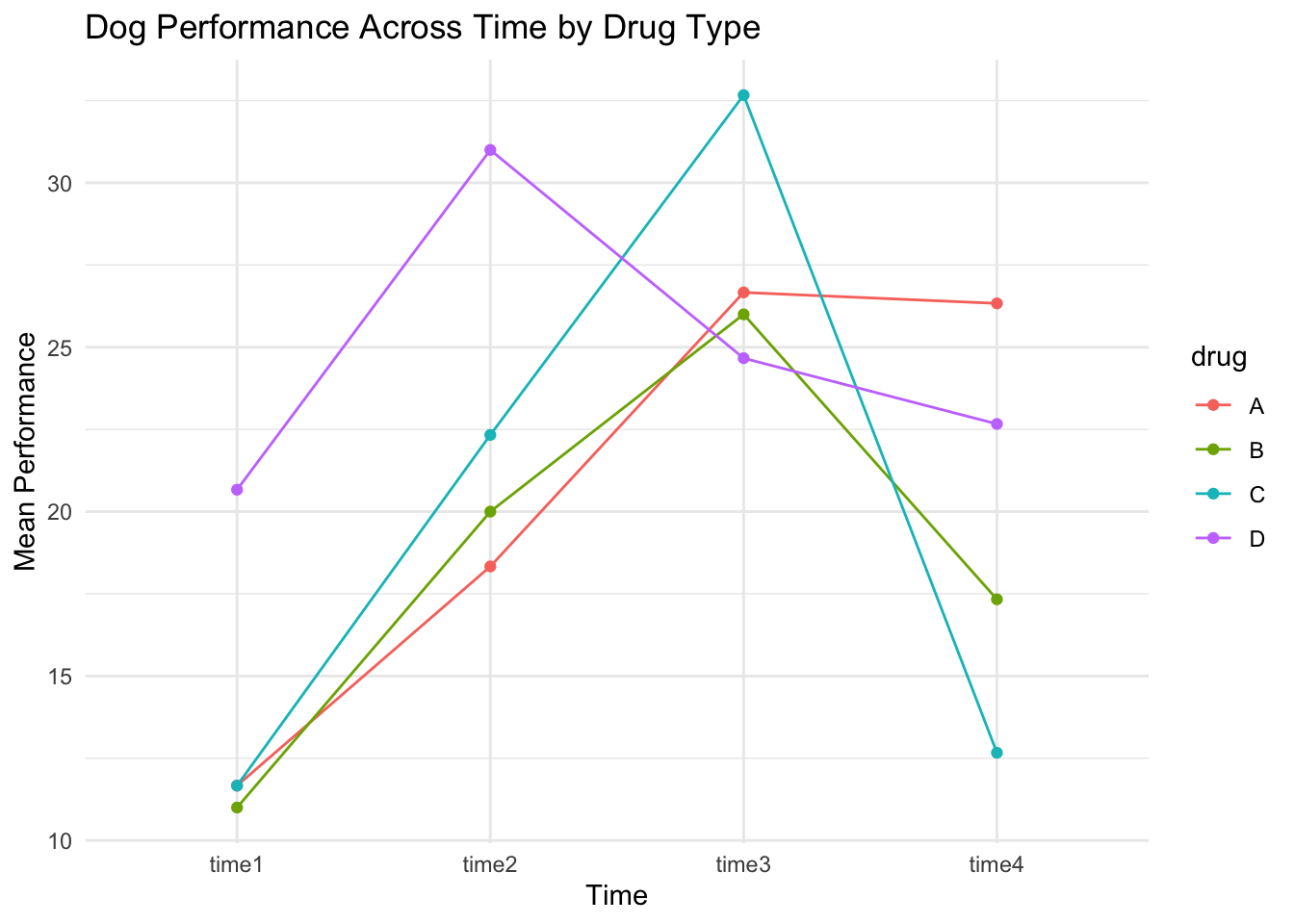
Click to see R code
# Create the data frame
df <- data.frame(
dog = 1:12,
time1 = c(10, 12, 13, 12, 11, 10, 10, 12, 13, 20, 21, 21),
time2 = c(16, 19, 20, 18, 20, 22, 22, 23, 22, 30, 31, 32),
time3 = c(25, 27, 28, 25, 26, 27, 31, 34, 33, 24, 25, 25),
time4 = c(26, 25, 28, 15, 18, 19, 11, 14, 13, 21, 24, 23),
drug = c("A", "A", "A", "B", "B", "B", "C", "C", "C", "D", "D", "D")
)
# View the data frame
df dog time1 time2 time3 time4 drug
1 1 10 16 25 26 A
2 2 12 19 27 25 A
3 3 13 20 28 28 A
4 4 12 18 25 15 B
5 5 11 20 26 18 B
6 6 10 22 27 19 B
7 7 10 22 31 11 C
8 8 12 23 34 14 C
9 9 13 22 33 13 C
10 10 20 30 24 21 D
11 11 21 31 25 24 D
12 12 21 32 25 23 D